非最小相位系统的伯德图分析

如果系统传递函数的零点和极点均不在s平面的右半部，则称该系统为最小相位系统，否则，称为非最小相位系统。“最小相位”术语可做如下解释：在几个系统的传递函数中，如果它们的幅频特性完全相同，则对于任意频率，其中右半s平面没有零点和极点的传递函数，其相频特性的绝对值是最小的。

不稳定惯性环节G（s）=就是一个非最小相位系统，其频率特性为

对数幅频特性和对数相频特性分别为

其对数频率特性示于图5.3.10中。由图可见，其对数幅频特性曲线与惯性环节的对数幅频特性曲线一致。

再如，延迟环节G（s）=e-τs也是一个非最小相位系统，其频率特性为

延时环节的对数幅频特性和对数相频特性分别为

根据上式绘出延时环节的对数频率特性如图5.3.11所示，由图可知，延时环节的对数幅频特性是与横轴重合的直线，对数相频特性随ω增加而滞后增加。当ω=1/τ时，φ（ω）=-57.3°；当ω→∞时，φ（ω）→-∞。

【例5.3.2】试比较下面两系统的对数幅频特性和对数相频特性。

图5.3.10　不稳定惯性环节的伯德图

（a）幅频图；（b）相频图

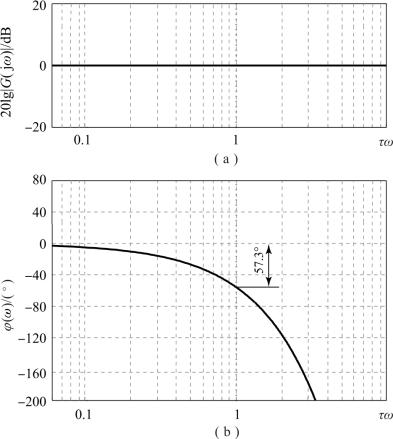
图5.3.11　延时环节的伯德图

（a）幅频图；（b）相频图(www.xing528.com)

式中，0＜Τ1＜Τ2。

【解】图5.3.12（a）、（b）分别示出了Ga（s）和Gb（s）的零极点图。

从零极点图可知，Ga（s）为最小相位系统，Gb（s）为非最小相位系统。它们的对数频率特性曲线如图5.3.13所示。La（ω）=Lb（ω），并在所有的频率范围内，。

图5.3.12　例5.3.2的两个系统的零极点图

（a）Ga（s）的零极点图；（b）Gb（s）的零极点图

图5.3.13　例5.3.2的两个系统的伯德图

（a）幅频图；（b）相频图

【例5.3.3】试比较下面两系统的对数幅频特性和对数相频特性。

图5.3.14　例5.3.3的两个系统的伯德图

（a）幅频图；（b）相频图

【解】显然Ga（s）为最小相位系统。当工作频率满足ω≪1/τ时，Gb（s）可做如下Pade近似

因此Gb（s）是非最小相位系统，它们的伯德图如图5.3.14所示。从图5.3.14可以看出：La（ω）=Lb（ω），对所有的频率范围内，，φb（ω）=φa（ω）-57.3τω。