典型环节的伯德图分析

1.比例环节

比例环节的传递函数为

其对数幅频特性和对数相频特性分别是

其伯德图如图5.3.1所示。由图可见，比例环节的对数幅频特性是一条纵坐标为20lg K、平行于横轴的直线，对数相频特性为与横轴重合的直线。因此，改变K值只能使对数幅频特性上升或下降，而对数相频特性不变。

图5.3.1　比例环节的伯德图

（a）幅频图；（b）相频图

2.积分环节

积分环节的传递函数为

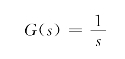
其频率特性为

对数幅频特性和相频特性分别为

可知，积分环节的对数幅频特性为过横轴ω=1处、斜率为

的直线，对数相频特性与ω无关，其值为恒等于-90°的直线。积分环节的伯德图如图5.3.2所示。

图5.3.2　积分环节的伯德图

（a）幅频图；（b）相频图

3.微分环节

微分环节的传递函数为

其频率特性为

对数频率特性和相频特性分别为

微分环节的伯德图如图5.3.3所示。由图可知，微分环节的对数幅频特性为过横轴ω=1处、斜率等于20 dB/dec的直线，对数相频特性为恒等于90°的直线。

图5.3.3　微分环节的伯德图

（a）幅频图；（b）相频图

可以看出，微分环节的对数频率特性是积分环节对数频率特性的负值，它们的伯德图关于横轴对称。

4.惯性环节

惯性环节的传递函数为

其频率特性为

对数幅频特性为

当Tω≤1，即ω≤1/T时，L（ω）≈0dB，它是与横轴重合的直线；当Tω≥1，即ω≥时，有

它是一条斜率为-20dB/dec、与横轴交于ω=1/T的直线。上述两直线为对数幅频特性的渐近线，由此两直线构成的折线称为惯性环节的渐近对数幅频特性曲线，两直线的交点ω=1/T称为交接频率，或称为转折频率。

惯性环节的准确对数幅频特性表达式减去渐近对数幅频特性表达式，得其误差表达式为

误差最大值出现在ω=1/T处，其数值为

图5.3.4绘出了惯性环节的对数幅频特性，图中的虚线为准确的特性曲线。一般情况下，工程上可直接使用渐近特性。如果要求曲线精度较高，可先画出渐近特性，然后再对ω=ωn=1/T附近进行修正而得到准确的曲线。由图5.3.4可以看出，惯性环节具有高频幅值衰减特性。因此，可以把数学模型为惯性环节的元件称为低通滤波器。

图5.3.4　惯性环节的伯德图

（a）幅频图；（b）相频图(www.xing528.com)

惯性环节的相频特性为

根据式（5.3.2）逐点描绘出的惯性环节对数相频特性曲线如图5.3.4（b）所示。惯性环节伯德图的一个重要性质是：其对数幅频和对数相频特性图的形状与时间常数T无关，当T改变时，其曲线只是随着横坐标上点1/T的位置左右移动，而整条曲线的形状保持不变。

5.一阶微分环节

一阶微分环节的传递函数为

其频率特性为

对数幅频特性和对数相频特性分别为

比较式（5.3.1）、式（5.3.2）和式（5.3.3）、式（5.3.4）可知，一阶微分环节的对数频率特性是惯性环节对数频率特性的负值，即一阶微分环节的对数幅频特性、对数相频特性分别与惯性环节的对数幅频特性、对数相频特性对称于横轴。一阶微分环节的对数频率特性如图5.3.5所示。

图5.3.5　一阶微分环节的伯德图

（a）幅频图；（b）相频图

6.振荡环节

振荡环节的传递函数为

其频率特性为

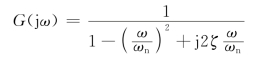
其幅频特性和相频特性为

振荡环节的对数幅频特性为

当ω/ωn≪1，即ω≪ωn时，有

它是一条与横轴重合的直线。

当ω/ωn≫1，即ω≫ωn时，有

它是一条斜率为-40 dB/dec、交横轴于ωn的直线。上述两直线是振荡环节对数幅频特性的渐近线，由此两直线衔接起来所构成的折线称为振荡环节的渐近对数幅频特性，两直线的交点ωn称为交接频率。图5.3.6示出了振荡环节渐近对数幅频特性曲线和按式（5.3.7）绘制的准确曲线。振荡环节的对数相频特性曲线随ζ值而异，但ω=ωn处的数值相同，其值为φ（ωn）=-90°。

当ω=0时φ（ω）=0°；当ω→∞时，φ（ω）=-180°。

图5.3.6　振荡环节的伯德图

（a）幅频图；（b）相频图

由图5.3.6可以看出，渐近对数幅频特性曲线与准确曲线在ωn附近存在误差，此误差与ζ值有关。准确特性的表达式减去渐近特性表达式可得误差表达式为

当ω=ωn时，δ（ω）=-20lg（2ζ）。

根据式（5.3.8）绘出的误差曲线如图5.3.7所示。从图5.3.7可知，当0.4＜ζ＜0.7时，δ（ω）＜4dB；当ζ值在0.4＜ζ＜0.7范围之外时，δ（ω）的最大值将增加，特别在ζ＜0.4时，ζ（ω）的最大值随ζ的减小显著增加；当ζ→0时，δ（ω）→∞。

因此，在满足条件0.4＜ζ＜0.7时，工程上可直接使用渐近对数幅频特性；在此范围之外，应使用准确的对数幅频特性。准确的对数幅频特性可在渐近对数幅频特性的基础上，用图5.3.7所示的误差曲线修正而获得，或应用式（5.3.8）直接计算。

图5.3.7　对数幅频特性误差曲线

7.二阶微分环节

传递函数为

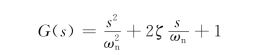
其频率特性为

二阶微分环节的传递函数是二阶振荡环节的倒数，因此二阶微分环节的对数频率特性是二阶振荡环节的负值，即它们的幅频和相频特性分别关于实轴对称，按对称性可得二阶微分环节的伯德图如图5.3.8所示。二阶微分环节对数幅频的渐近线，当ω≪ωn时，是一条与横轴重合的直线；当ω≫ωn时，是一条斜率为40 dB/dec、交横轴于ωn的直线，ωn称为交接频率或者转折频率。

图5.3.8　二阶微分环节的伯德图

（a）幅频图

图5.3.8　二阶微分环节的伯德图（续）

（b）相频图