频率特性的几何表示法详解

1.幅相频率特性图

频率特性G（jω）是一个复数，它可以表示成模与辐角的形式，也可以表示成实部与虚部

它们之间的关系可由图5.2.4所示的矢量图得到，即

当频率ω从零至无穷大变化时，频率特性的模和辐角均随之变化，图5.2.4的矢量端点便在复平面上画出一条轨迹，这条轨迹表示出模与辐角之间的关系，ω为参变量，通常这条曲线简称为幅相曲线或奈奎斯特（Nyquist）曲线，而这个图形称为幅相频率特性图或奈奎斯特图，也称为极坐标图。由于幅频特性为频率ω的偶函数，相频特性为ω的奇函数，则ω从零变化到+∞与ω从零变化到-∞的幅相曲线关于实轴对称，因此一般只绘制ω从零变化至+∞的曲线。在系统幅相曲线中，频率ω为参变量，一般用小箭头表示ω增大时幅相曲线的变化方向。如图5.2.1所示的RC网络的幅频特性和相频特性分别为

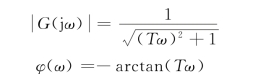
当ω=0时，=1，φ（ω）=0°；随ω的数值增加，减小，φ（ω）向负的方向增加，当ω=1/T时，=0.707，φ（ω）=-45°；当ω→∞时，=0，φ（ω）=-90°。如图5.2.5为该RC网络的幅相频率特性曲线。

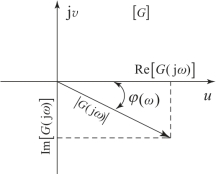
图5.2.4　频率特性的幅值与相位示意图

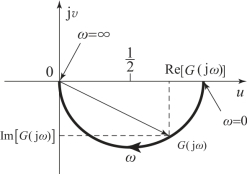
图5.2.5　RC网络的幅相频率特性曲线

可以证明，RC网络的幅相频率特性曲线是以（1/2，0）为圆心、半径为1/2的半圆。

2.对数频率特性图

对数频率特性图又称为伯德（Bode）图，包括对数幅频和对数相频两条曲线，是工程中广泛使用的一组曲线。对数频率特性曲线的横坐标是频率ω，按lgω均匀分度，单位是rad/s。对数幅频曲线的纵坐标按L（ω）=20lg线性分度，单位是分贝（dB）。对数相频特性曲线的纵坐标表示相频特性的函数值，线性分度，单位为度（°）。(www.xing528.com)

对数分度和线性分度如图5.2.6所示。在线性分度中，当变量增大或减小1时，坐标间距离变化一个单位长度；而在对数分度中，当变量增大或减小10倍时，称为十倍频程（dec），坐标间距离变化一个单位长度。表5.2.1给出了十倍频程的对数分度。

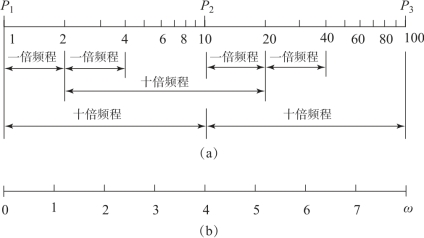
图5.2.6　对数分度与线性分度

（a）对数分度；（b）线性分度

表5.2.1　十倍频程中的对数分度

图5.2.1所示RC网络的对数频率特性如图5.2.7所示。

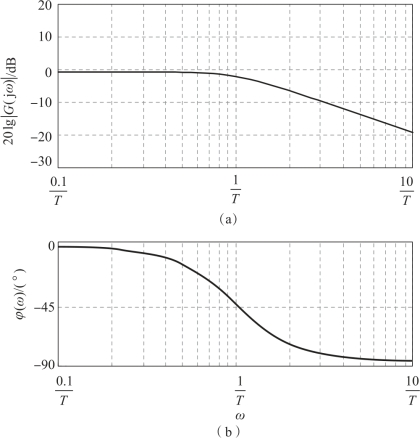
图5.2.7　RC网络的伯德图

（a）幅频图；（b）相频图

根据伯德图研究系统频率特性的优点是：动态补偿设计可完全基于伯德图来完成；伯德图可通过实验的方法完成绘制；对数幅频特性采用，将幅值的乘除运算转化为加减运算，所以系统伯德图可通过简单的曲线叠加来完成，非常简便；因为伯德图的横坐标是以对数分度的，所以可比线性分度表示更大的频率范围。

3.对数幅相图

对数幅相图又称尼科尔斯（Nichols）图，其纵坐标为L（ω），单位为分贝（d B），横坐标为φ（ω），单位为度（°），均为线性分度，频率ω为参变量。

在上述三种频率特性的几何表示方法中，伯德图的作图最为方便，工程上经常使用。