频率特性基本概念

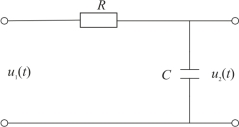
图5.2.1　RC滤波网络

首先以图5.2.1所示的RC滤波网络为例，建立频率特性的基本概念。假设电容C两端的初始电压为零，如果网络的输入电压为

输入电压的拉氏变换为

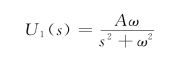
RC滤波网络的传递函数为

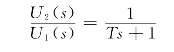
则RC滤波网络的输出电压为

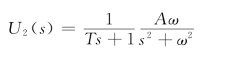
进行拉氏反变换，可得电容两端电压为

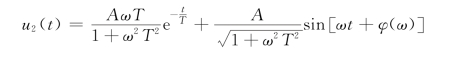
其中，φ（ω）=-arctan（ωT），第一项为输出电压的瞬态分量，随时间增大而趋于零；第二项正弦信号为输出电压的稳态分量，与输入电压同频率，但振幅和相位与输入信号不同，即稳态输出电压的时域表达式为

(www.xing528.com)

上式表明，对于稳定的线性定常系统，由谐波输入产生的系统输出的稳态量依然是与输入信号同频率的谐波信号，而幅值和相位的变化量是频率ω的函数，且与系统的数学模型有关。

注意到RC网络的传递函数为G（s）=，取s=jω，则有

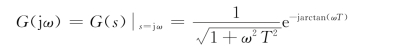
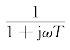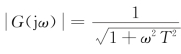可见，RC网络稳态输出电压与输入电压幅值之比为G（jω）的幅值，RC网络稳态输出电压与输入电压相位之差为G（jω）的相角∠G（jω）。这一结论非常重要，反映了幅值和相位的变化与系统数学模型的本质关系，具有普遍性。因为完整描述了RC网络在正弦输入电压作用下，稳态输出的电压幅值和相角随正弦输入电压频率ω的变化规律，所以称G（jω）=为RC滤波网络的频率特性，而称为该网络的幅频特性，φ（ω）=-arctan（ωT）为该网络的相频特性。频率特性与传递函数相比较得

图5.2.2给出了线性定常系统G（s）在正弦输入作用下的稳态输出曲线。

图5.2.2　线性定常系统在正弦输入作用下的稳态输出曲线

若系统的输入信号为正弦函数，则系统输出的稳态分量也是同频率的正弦函数，其幅值放大了倍，相位移动了φ（ω）=∠G（jω），和φ（ω）都是频率的函数，输出与输入的振幅比值称为系统的幅频特性，输出与输入的相位差φ（ω）称为系统的相频特性，而复数G（jω）=称为系统的频率特性。

频率特性与传递函数的关系为

频率特性与传递函数一样，表示了系统的运动特性，是数学模型的一种表示形式。微分方程、传递函数和频率特性三种描述方法的关系可用图5.2.3说明，图中的p为微分算子。

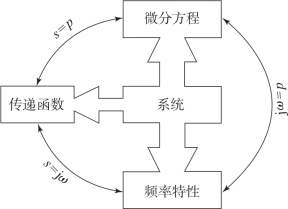
图5.2.3　频率特性、传递函数和微分方程等三种系统描述之间的关系