增加开环极点或零点对根轨迹的影响探究

根轨迹与开环传递函数的极点和零点直接相关，所以增加一个开环极点或增加一个开环零点必然会使根轨迹移动，从而使闭环极点的位置发生变化。用根轨迹方法对系统进行校正，实际上就是为校正器传递函数选择合适的极点和零点，以使闭环系统的极点位于希望的位置。所以，了解增加一个开环极点或者开环零点对根轨迹的影响，对选择校正器传递函数的极点和零点具有重要的指导作用。

例如，开环传递函数

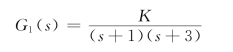
的根轨迹很简单，是图4.5.1中的虚线和（-3，-1）之间的线段。

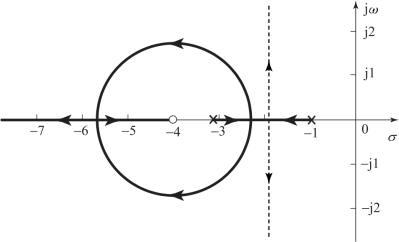
图4.5.1　附加零点的一般影响

开环传递函数

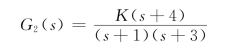
的根轨迹如图4.5.1中的实线所示。

对照G1（s）与G2（s）的根轨迹可以发现，G2（s）增加一个零点后，根轨迹向左方移动，改善了系统的稳定性，增加开环零点相当于给系统加了一个比例-微分控制器。

开环传递函数

的根轨迹如图4.5.2中的实线所示。

对照G1（s）与G3（s）的根轨迹可以发现，增加一个极点后，根轨迹向右方移动，系统稳定性变差。

图4.5.1和图4.5.2针对特定系统显示了增加零点或极点对根轨迹的影响，但这种现象具有普遍性和一般意义。

图4.5.2　附加极点的一般影响

【例4.5.1】有一些重要的控制问题，例如卫星的姿态控制，其被控对象可以用双积分传递函数来描述，即Go（s）=。双积分环节的单位反馈控制系统如图4.5.3所示，试比较当控制器Gc（s）分别为比例控制器和比例-微分控制器时的根轨迹。

图4.5.3　双积分系统的单位反馈控制系统

【解】当控制器Gc（s）为比例控制器时，即Gc（s）=Kp，则系统的开环传递函数为G（s）=，以Kp为可变参数的根轨迹方程为

(www.xing528.com)

根据根轨迹绘制法则，可知闭环系统的根轨迹在虚轴上，所以无论Kp为何值，其过渡过程响应都是持续振荡的。

假设控制器为比例-微分控制器，即Gc（s）=Kp（Tds+1），假设Td=1，则系统的开环传递函数为G（s）=，闭环系统的根轨迹方程为

根据根轨迹绘制法则画出根轨迹如图4.5.4所示。

由图4.5.4可见，附加零点将根轨迹拉向了左半s平面，闭环系统变成稳定系统，比例微分控制改善了系统的动态性能和稳定性，可见设计控制器的重要性。

在2.5节中，我们提到纯微分在实际物理系统中是不可实现的，实际中常用近似微分环节代替纯微分环节，即Gc（s）=。

图4.5.4　开环传递函数为G（s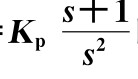）=时的系统根轨迹

令K=Kp+p KpTd，z=p Kp/K，则Gc（s）=，系统的开环传递函数为G（s）=，闭环系统的根轨迹方程为

假设z=1，p=12，则根轨迹方程为

根据根轨迹绘制法则画出的根轨迹如图4.5.5所示。

由图可见，相比图4.5.4，附加的极点使系统根轨迹发生了变化，但是在原点附近，图4.5.5与图4.5.4的根轨迹还是很相似的。

现在我们将附加极点向右移动，使之靠近原点。假设p=4，即根轨迹方程为

根据根轨迹绘制法则画出的根轨迹如图4.5.6所示。

由图4.5.6可见，系统的根轨迹相比p=12的系统的根轨迹（图4.5.5）发生了很大改变，根轨迹不再有分离点；而且由根之和法则可知，闭环系统特征根的重心向右移动，即系统的稳定程度下降，这一点从图4.5.6中也很容易看出来。这说明附加极点越是接近虚轴，对系统的稳定程度影响越大。在本例题中，Gc（s）=（p＞z）就是我们第6章要讲到的超前校正器。

图4.5.5　开环传递函数为G（s）=K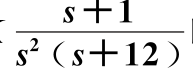时的系统根轨迹

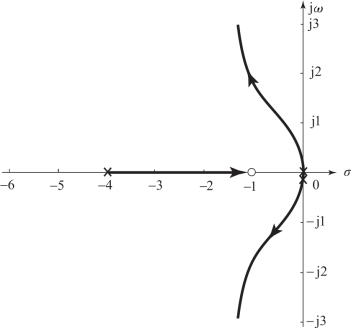
图4.5.6　开环传递函数为G（s）=K）时的系统根轨迹