参量根轨迹分析自动控制系统中的变化参数及影响

在用根轨迹分析自动控制系统时，最常用的参变量是K*，但有时也取其他参数为变化参量，这时所绘制的根轨迹称为参量根轨迹。绘制参量根轨迹的方法是，首先写出系统的闭环特征方程

然后对此方程进行变换，将其化成下面形式

式中，ρ是根轨迹所使用的变化参量，ρG1（s）是以s为自变量的函数，称为等效开环传递函数。这时，可以继续使用以K*为变化参量的根轨迹绘制法则，下面举例说明。

【例4.4.1】若反馈控制系统的结构图如图4.4.1所示，试画出以速度负反馈系数τ为参变量的根轨迹，并讨论速度负反馈对系统过渡过程的影响。

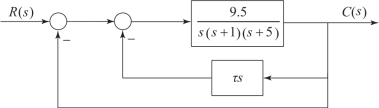
图4.4.1　例4.4.1的控制系统

【解】（1）求等效开环传递函数。

闭环系统特征方程为

（2）绘制以τ*为参变量的根轨迹。

①在图4.4.2上标出等效开环传递函数的零极点：

②n=3，m=1时，有3条根轨迹，当τ*→∞时，其中一条趋于零点z=0，其他两条趋于无穷远。

③根轨迹的渐近线。

渐近线与实轴的交点为

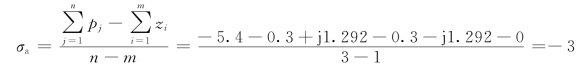
渐近线与实轴的交角为(www.xing528.com)

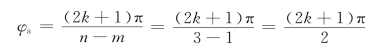
当k=0时，φa1=π/2；当k=-1时，φa2=-π/2。

④实轴上的根轨迹。

在（-5.4，0）区间之右仅有一个实数零点，故此区间实轴是根轨迹。

⑤求复数极点p2和p3的起始角。

z，p1，p3指向p2的矢量辐角分别为

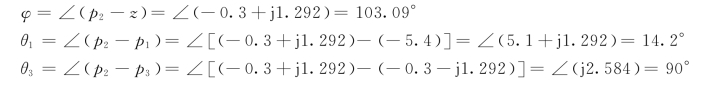
根据式（4.3.23）有

由根轨迹的对称性，可得

通过以上五步绘制的以τ*为参变量的根轨迹如图4.4.2所示。

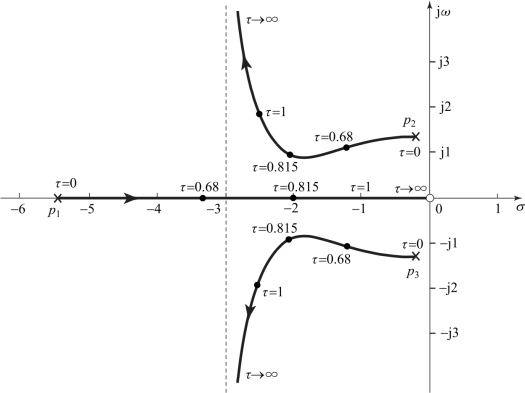
图4.4.2　例4.4.1的根轨迹

（3）速度负反馈对系统过渡过程的影响。

由图4.4.2可知，当τ*=0时，原系统为三阶系统，闭环系统有一个负实数极点和一对共轭复数极点，实数极点与共轭复数极点至虚轴的距离之比为5.4/0.3=18，所以它是一个以p2和p3为主导极点的等效二阶系统；当τ*增大时，即速度负反馈增大时，共轭复数极点左移，ωn增大，ζ增大，同时实数极点右移，这样会使系统单位阶跃响应的超调量σp%下降，调节时间ts缩短。当τ*=7.75，即τ=0.815时，共轭复数极点与实数极点距虚轴的距离相等，超调量σp%会下降至很小，同时调节时间ts也会很小。当继续增大τ*时，即继续增大速度负反馈时，实数极点距虚轴的距离比复数极点近，系统具有一阶系统的特征，超调量σp%=0，且随τ*增大，ts增大；当τ*→∞时，实数极点接近坐标原点，此时系统反应很迟钝，ts很大。速度反馈系数τ值不同时的系统单位阶跃响应曲线如图4.4.3所示。

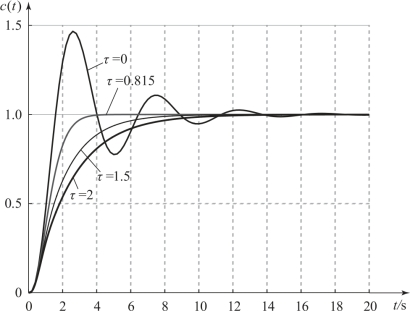
图4.4.3　速度反馈系数不同时的系统单位阶跃响应