稳态误差在扰动作用下的影响

除参考输入信号外，控制系统的外作用还有各种扰动。例如，负载转矩的变动、放大器的零位和噪声、电源电压和频率的波动、组成元件的零位输出，以及环境温度的变化等。控制系统在扰动作用下的稳态误差值，反映了系统的抗干扰能力。在理想情况下，系统对于任意形式的扰动作用的稳态误差应该为零，但实际上这是不可能实现的。

由于输入信号和扰动信号作用于系统的不同位置，因此即使系统对于某种形式的输入信号的稳态误差为零，但对于同一形式的扰动作用，其稳态误差未必为零。设控制系统如图3.10.8所示，其中D（s）代表扰动信号的拉氏变换。由于在扰动信号D（s）作用下，系统的理想输出应为零，故该非单位反馈系统的输出端误差信号为

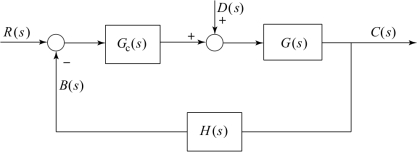
图3.10.8　控制系统

当sEd（s）在右半s平面及虚轴上解析时，同样可以采用终值定理法来计算系统在扰动作用下的稳态误差，即为

【例3.10.4】设比例控制系统如图3.10.9所示。图中，R（s）=R0/s为阶跃输入信号；M（s）为比例控制器输出转矩，用以改变被控对象的位置；D（s）=d0/s为阶跃扰动转矩。试求系统的稳态误差。

图3.10.9　比例控制系统

【解】由图3.10.9可见，本例系统为Ⅰ型系统。令扰动D（s）=0，则系统对阶跃输入信号的稳态误差为零。但是，如果令R（s）=0，则系统在扰动作用下输出量的实际值为

而扰动作用下系统输出量的期望值为零，因此误差信号为

系统在阶跃扰动转矩作用下的稳态误差为

系统在阶跃扰动转矩作用下存在稳态误差的物理意义是明显的。稳态时，比例控制器产生一个与扰动转矩d0大小相等而方向相反的转矩-d0以进行平衡，该转矩折算到比较装置输入端的数值为-d0/K1，所以系统必定存在常值稳态误差-d0/K1。

【例3.10.5】如果在例3.10.4系统中采用比例-积分控制器，如图3.10.10所示，试分别计算系统在阶跃转矩扰动和斜坡转矩扰动作用下的稳态误差。

(www.xing528.com)

图3.10.10　比例-积分控制系统

【解】由图3.10.10可知，该比例-积分控制系统对扰动作用为Ⅰ型系统，在阶跃扰动作用下不存在稳态误差，而在斜坡扰动作用下存在常值稳态误差。

由图3.10.10不难写出扰动作用下的系统误差表达式为

假设sEd（s）的极点位于左半s平面，则可用终值定理法求得稳态误差。

当D（s）=d0/s时，得

当D（s）=d0/s2时，得

显然，提高比例增益K1可以减小斜坡转矩作用下的稳态误差，但K1的增大要受到稳定性要求和动态过程振荡性要求的制约。

系统采用比例-积分控制器后，可以消除阶跃扰动转矩作用下的稳态误差，其物理意义是清楚的：由于控制器中包含积分控制作用，只要稳态误差不为零，控制器就一定会产生一个继续增长的输出转矩来抵消阶跃扰动转矩的作用，力图减小这个误差，直到稳态误差为零，系统取得平衡而进入稳态。在斜坡转矩扰动作用下，系统存在常值稳态误差的物理意义可以这样解释：由于转矩扰动是斜坡函数，因此需要控制器在稳态时输出一个反向的斜坡转矩与之平衡，这只有在控制器输入的误差信号为一负常值时才有可能。实际系统总是同时承受输入信号和扰动作用的，由于所研究的系统为线性定常控制系统，因此系统总的稳态误差就等于输入信号和扰动分别作用于系统时，所得的稳态误差的代数和。

如何减小或者消除扰动引起的稳态误差呢？可以采取以下措施：

（1）增大扰动作用点之前系统的前向通道增益。

由例3.10.4可知，增大扰动作用点之前系统的前向通道增益K1，可以减小系统对阶跃扰动转矩的稳态误差。式（3.10.19）表明，系统在阶跃扰动转矩作用下的稳态误差与K无关，因此，增大扰动点之后系统的前向通道增益，不能改变系统对扰动的稳态误差数值。

（2）在扰动作用点之前的前向通道或主反馈通道中设置v个积分环节。

如图3.10.8所示，如果在扰动作用点之前的前向通道（即Gc（s））或主反馈通道（即H（s））中设置v个积分环节，可消除系统在扰动信号d（t）=作用下的稳态误差。由例3.10.5可知，在扰动作用点之前的前向通道中增加一个积分环节，消除了系统在阶跃扰动转矩作用下的稳态误差。

同样需要注意，为了减小或者消除扰动引起的稳态误差而在反馈控制系统中设置串联积分环节或增大开环增益的措施，会降低系统的稳定性，甚至造成系统不稳定。

无论对于有用输入信号R（s）还是扰动信号D（s），还可以采用复合控制的方式减小或者消除稳态误差。尤其是当控制系统中存在强扰动，特别是低频强扰动时，一般的反馈控制方式难以满足系统高稳态精度的系统要求，此时可以采用复合控制方式。复合控制系统是在系统中加入前馈通路，组成一个前馈控制与反馈控制相结合的系统，只要系统参数选择合适，不但可以保持系统稳定，而且能极大地减小乃至消除稳态误差。详见本书第6章6.9节。