非单位反馈系统稳态误差优化方法

由于需要加入补偿器以提高系统性能或者是物理系统本身的原因，控制系统并不总是单位反馈形式，反馈回路可能是增益或者是一个动态模型。

设非单位反馈控制系统结构图如图3.10.5所示。

图3.10.5　非单位反馈控制系统的方框图

Ea（s）并不是输入信号与输出信号之间的误差，而是系统用来产生控制作用的误差信号，我们称之为驱动信号（Actuating Signal）。如果r（t）与c（t）具有相同的单位，那么可以求得系统的稳态误差为e（∞）=r（∞）-c（∞）。

可以直接利用终值定理求出e（∞），求法如下：

若需要求出系统对应的静态误差系数，则需要对非单位反馈控制系统的方框图进行等效变换，将E（s）=R（s）-C（s）在框图中表示出来。

将图3.10.5等效变换为图3.10.6（a），再变换为图3.10.6（b），就可以得到等效的单位反馈回路，如图3.10.6（c）所示，其显式地描述了E（s）=R（s）-C（s），且

(www.xing528.com)

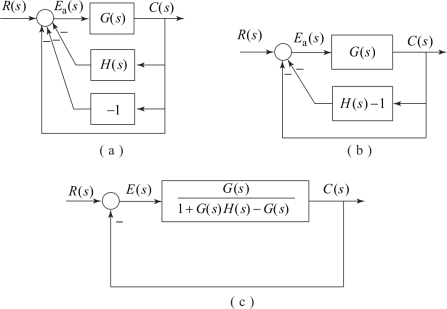
图3.10.6　将非单位反馈系统等效变换为单位反馈系统

（a）等效变换一；（b）等效变换二；（c）等效的单位反馈回路

接下来就可以用3.10.2节单位反馈系统的方法求系统的稳态误差和静态误差系数了。

【例3.10.3】控制系统框图如图3.10.7所示，误差定义为e（t）=r（t）-c（t），确定系统的类型，并计算系统的静态误差系数和单位阶跃输入下系统的稳态误差，进一步求出单位阶跃和单位斜坡输入下，驱动信号Ea（s）的稳态值。

图3.10.7　某非单位反馈系统的框图

系统稳态误差为负值，说明输出信号比输入信号大。

若输入为单位斜坡函数，则系统稳态误差为无穷大。