三种标准测试输入信号下的稳态误差分析与优化

1.阶跃输入作用下的稳态误差与静态位置误差系数

对幅值为A的阶跃输入，系统的稳态误差为

于是对零型系统，ν=0，稳态误差为

常数G（0）通常记为Kp，称为静态位置误差常数。它由下式给出

于是零型系统对幅值为A的阶跃输入的稳态跟踪误差为

而对ν≥1的各型系统，其阶跃响应的稳态误差为零，因为Kp=∞，即

2.斜坡输入作用下的稳态误差与静态速度误差系数

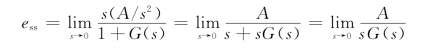
对斜率为A的斜坡输入，系统稳态误差为同样，稳态误差取决于系统的积分器个数ν。对于零型系统，ν=0，稳态误差为无穷大。

对于Ⅰ型系统，ν=1，稳态误差为

其中，Kv称为静态速度误差系数。它由下式给出

如果传递函数有多个积分器，即ν≥2，则稳态误差为零。

3.加速度输入作用下的稳态误差与静态加速度误差系数

当系统的输入为r（t）=At2/2时，稳态误差为

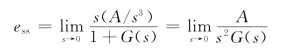
对于至多含一个积分器的系统，稳态误差为无穷大；若系统含两个积分器，即ν=2，则可得

其中，Ka称为静态加速度误差常数，它由下式给出

如果积分器个数等于或超过3，则系统的稳态误差为零。控制系统的稳态误差小结见表3.10.1。

表3.10.1　稳态误差小结

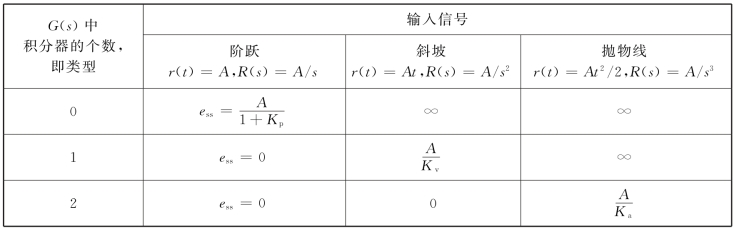
应当指出，在系统误差分析中，只有当输入信号是阶跃函数、斜坡函数和加速度函数，或者是这三种函数的线性组合时，静态误差系数才有意义。用静态误差系数求得的系统稳态误差值，或是零，或是常值，或趋于无穷大。当系统输入信号为其他形式函数时，静态误差系数便无法应用。

【例3.10.1】计算如图3.10.2所示系统的静态误差系数，以及单位阶跃、单位斜坡、单位加速度输入信号作用下的稳态误差。

【解】经验证，闭环系统稳定。因此

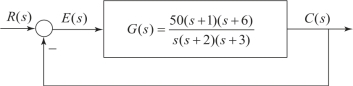
图3.10.2　例3.10.1的框图(www.xing528.com)

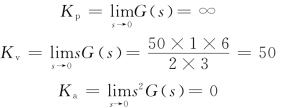
单位阶跃输入作用下系统的稳态误差为

单位斜坡输入信号下系统的稳态误差为

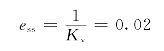
单位加速度输入信号下系统的稳态误差为

4.静态误差系数的内涵

静态误差系数Kp、Kv、Ka定量地描述了系统跟踪不同形式输入信号的能力，能够表征系统减小或消除稳态误差的能力。正如上升时间、峰值时间、调节时间和超调量是系统的动态性能指标一样，静态误差系数可以作为系统稳态性能的衡量指标，静态误差系数中蕴含了丰富的系统信息。

例如，如果一个系统的Kp=90，那么我们可以得到以下结论：

（1）该系统是稳定的。

（2）该系统是零型系统，因为只有零型系统的Kp值才为有限值，Ⅰ型及以上系统的Kp=∞。

（3）阶跃函数是该系统的测试信号。因为Kp是有限值，而且阶跃信号作用下的稳态误差为ess=，因此我们知道测试输入信号是阶跃函数。

（4）该系统在单位阶跃函数作用下的稳态误差是ess==1/91。

【例3.10.2】移动机器人可以帮助严重残障人士行驶，这种机器人的驾驶控制系统可用图3.10.3来表示。系统的控制器为Gc（s）=K1+K2/s，试求控制系统的稳态误差。

图3.10.3　移动机器人驾驶控制系统框图

【解】当K2=0时，Gc（s）=K1时，系统对阶跃输入的稳态误差为

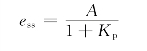
其中Kp=KK1。

当K2＞0时，得到Ⅰ型系统：

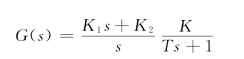
此时系统对阶跃输入的稳态误差为0。如果驾驶命令为斜坡输入，则系统的稳态误差为

其中，

当Gc（s）=K1+K2/s时，系统对锯齿波输入的动态响应如图3.10.4所示。

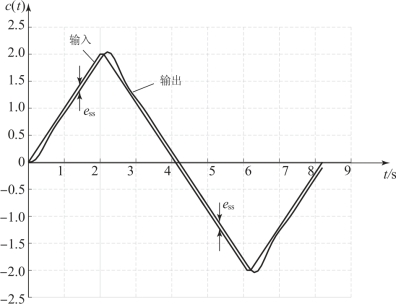
图3.10.4　移动机器人驾驶控制系统的锯齿波响应

如果Kv足够大，那么稳态误差是可以忽略的。

针对特定的系统，设计者既要增加误差系数以便控制稳态误差，又必须注意维持较好的瞬态性能。就例3.10.2而言，可以通过增加增益因子KK2，即增加Kv来减小稳态误差，但是KK2的增加会减小阻尼比ζ，使系统的阶跃响应振荡更严重。所以折中方案是在保证ζ不小于容许值的基础上，尽量选择较大的Kv。

如何减小或者消除单位反馈系统的稳态误差呢？由式（3.10.6）可知：

（1）增大系统的开环增益，可以减小系统的稳态误差；

（2）增加系统积分环节的数目，可消除系统的稳态误差。

但是，在反馈控制系统中，设置串联积分环节或增大开环增益以消除或减小稳态误差的措施，必然会降低系统的稳定性，甚至造成系统不稳定，从而恶化系统的动态性能。因此，权衡考虑系统稳定性、稳态误差与动态性能之间的关系，便成为系统校正设计的主要内容。