单位反馈系统稳态误差优化方案

1.误差与稳态误差

尽管引入反馈会增加成本和系统的复杂性，但它能明显减小系统的稳态误差，这是在系统中引入反馈的基本原因之一，闭环系统的稳态误差比开环系统小几个数量级。

设单位反馈控制系统结构图如图3.10.1所示，由图可得

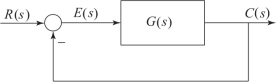
图3.10.1　反馈控制系统

通常，称E（s）为误差信号，简称误差（亦称偏差）。

误差本身是时间的函数，其时域表达式为

式中，Φe（s）为系统误差传递函数，即

在误差信号e（t）中，包含暂态（自由）分量ets（t）和稳态（受迫）分量ess（t）两部分。由于系统必须稳定，故当时间趋于无穷时，必有ets（t）趋于零。因而，控制系统的稳态误差定义为误差信号e（t）的稳态分量ess（∞），常以ess简单标志。

如果有理函数sE（s）除在原点处有唯一的极点外，在右半s平面及虚轴上解析，即sE（s）的极点均位于左半s平面（包括坐标原点）时，则可根据拉氏变换的终值定理，由式（3.10.4）方便地求出系统的稳态误差

由于上式算出的稳态误差是误差信号稳态分量ess（t）在t趋于无穷时的数值，故有时称为终值误差。(www.xing528.com)

熟悉系统在3种标准测试输入信号下的稳态误差是很有用的。

2.系统的类型

由稳态误差计算公式（3.10.4）可见，单位反馈控制系统稳态误差数值与开环传递函数G（s）的结构以及输入信号R（s）的形式密切相关，对于一个给定的稳定系统，当输入信号形式一定时，系统是否存在稳态误差就取决于G（s）。因此，按照控制系统跟踪不同输入信号的能力来进行系统分类是必要的。

在一般情况下，G（s）可表示为

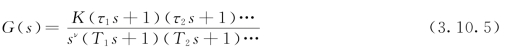
式中，K称为系统的开环增益，ν为开环系统在s平面坐标原点上的极点的重数。以ν的数值来划分系统的类型：ν=0，称为零型系统；ν=1，称为Ⅰ型系统；ν=2，称为Ⅱ型系统……。当ν＞2时，除非采用复合控制，否则使系统稳定是比较困难的。

这种以开环系统在s平面坐标原点上的极点数量来分类的方法，其优点在于：可以根据已知的输入信号形式，迅速判断系统是否存在稳态误差及稳态误差的大小。

为了便于讨论，令

必有s→0时，G0（s）→1，因此，式（3.10.5）可改写为

系统稳态误差计算通式（3.10.4）则可改为

式（3.10.6）表明，影响稳态误差的诸因素是：系统型别，开环增益，输入信号的形式和幅值。下面讨论不同型别系统在不同输入信号作用下的稳态误差计算。由于实际输入多为阶跃函数、斜坡函数和加速度函数，或者是其组合，因此只考虑系统分别在阶跃、斜坡或加速度函数输入作用下的稳态误差计算问题。