总体而言，极点的位置决定了闭环系统的瞬态响应模态，零点则决定了每个模态的相对权重。若将零点移动到某个特定极点的近旁，将降低该极点对系统响应的影响。如果系统极点在左半s平面，则无论系统极点是实数极点还是共轭复数极点，其对应的瞬态响应分量都是衰减的，且衰减的快慢取决于该极点距离虚轴的距离，极点离虚轴越远，衰减就越快。
一个高阶系统，如果存在靠近虚轴的实数极点或一对共轭复数极点，并且在其附近又无零点，其他极点或因远离虚轴而被忽略，或者因为成为偶极子而被忽略，则靠近虚轴的实数极点或这对共轭复数极点称为此高阶系统的闭环主导极点，它决定系统过渡过程的主要特征。由于欠阻尼情况的二阶系统有较好的过渡过程品质，所以在实际系统中常取主导极点为共轭复数。具有一对共轭复数主导极点的高阶系统，可用其主导极点所对应的二阶系统来近似，此二阶系统称为原高阶系统的等效二阶系统，并可通过对等效二阶系统的分析来估计原高阶系统的过渡过程性能指标。
【例3.8.1】若单位反馈系统开环传递函数为
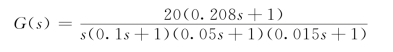
试求其单位阶跃响应。
【解】系统闭环传递函数为
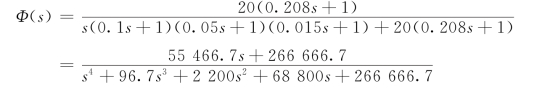
应用计算机解高阶代数方程方法求出闭环系统极点，并将上式写成下面因式相乘积形式
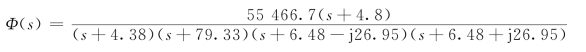
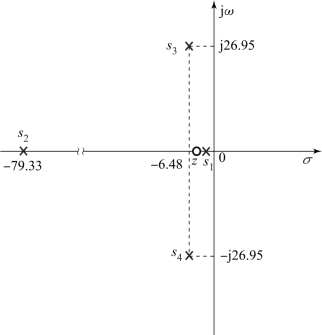
其闭环零极点示于图3.8.1。
(www.xing528.com)
图3.8.1 例3.8.1系统的闭环零极点图
系统单位阶跃响应的拉氏变换为
则得单位阶跃响应为
【例3.8.2】试求例3.8.1系统的等效二阶系统及其性能指标。
【解】由图3.8.1可见，最靠近虚轴的极点是s1=-4.38，但其附近有一零点z=-4.8，零极点之间的距离与s1至虚轴的距离之比为10.42，所以s1与z形成偶极子；而s2与s3至虚轴的距离之比为：79.33/6.48=12.48，s2对过渡过程的影响也可以忽略。因此本系统可以化成等效二阶系统。为使等效二阶系统与原系统有相同增益，需将原系统中要略去的因子化成典型环节形式后再简化。即
该高阶系统简化后的单位响应曲线如图3.8.2所示。
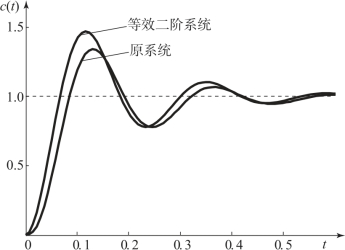
图3.8.2 高阶系统简化前和简化后的单位阶跃响应曲线
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
