【摘要】:一般在工程中,当附加极点至虚轴的距离大于原二阶系统的极点至虚轴的距离的5倍时,其对应的自由响应对过渡过程的影响就可以忽略了。而且附加极点越是远离虚轴,在系统阶跃响应中其对应的自由响应e-γt衰减得越快,在整个系统到达稳态之前其影响早已消失。
在典型二阶闭环系统上附加一个极点后,系统变为三阶系统,其传递函数为

s=-γ是附加极点。当ωn=1、ζ=0.5时,三阶系统各极点在复平面上的位置分布如图3.7.1所示。当γ分别为1、2.5、5时,三阶系统的单位阶跃响应如图3.7.2所示。

图3.7.1 三阶系统各极点在复平面上的位置分布
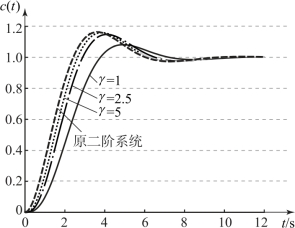
图3.7.2 三阶系统的单位阶跃响应(https://www.xing528.com)
由图可见,在二阶系统上附加极点后,系统的响应变慢,超调量变小,极点越是靠近虚轴,这种影响就越大。反之,当附加极点远离虚轴时,这个极点的影响就可以忽略,三阶系统就可以降为二阶系统。
通过对三阶系统的单位阶跃响应的像函数C(s)进行部分分式展开,观察各极点对应的留数,也会很容易理解为何可以忽略远离虚轴的极点。
三阶系统的单位阶跃响应的像函数为

其中留数D为
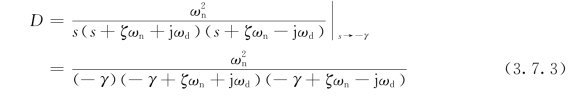
可见,附加极点越是远离虚轴,越是远离原二阶系统的极点,留数D就越小,这个极点的影响就越是可以忽略。而且附加极点越是远离虚轴,在系统阶跃响应中其对应的自由响应e-γt衰减得越快,在整个系统到达稳态之前其影响早已消失。一般在工程中,当附加极点至虚轴的距离大于原二阶系统的极点至虚轴的距离的5倍时,其对应的自由响应对过渡过程的影响就可以忽略了。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




