典型二阶系统的时域响应优化技巧

一阶系统很简单，改变其时间常数，只会改变其动态响应的速度，而响应模态不变。而改变二阶系统的参数，可能改变动态响应的模态，例如二阶系统可能呈现出与一阶系统类似的单调衰减的模态，也可能呈现出纯粹的振荡响应模态。

用二阶微分方程描述的系统称为二阶系统。从物理上讲，二阶系统包含两个储能元件，如第2章中提到的RLC网络、弹簧-质量块-阻尼器机械系统等，能量在两个储能元件之间交换，当阻尼不够大时，系统呈现出振荡的特性，所以二阶系统也称为二阶振荡环节。

二阶系统（见图3.4.1）的典型传递函数为

式中，ζ为阻尼系数，ωn为无阻尼自然振荡频率。

图3.4.1　标准形式的二阶系统结构图

二阶系统的典型传递函数也可以写成如下形式

式中，T=。

令式（3.4.1）的分母多项式为零，则二阶系统的特征方程为

其两个根（闭环极点）为

工程上常根据ζ的变化范围，分成4种情况讨论。

1.零阻尼（ζ=0）二阶系统的单位阶跃响应

当ζ=0时，二阶系统的特征方程有一对纯虚根。

此时，二阶系统的单位阶跃响应为

进行拉氏反变换得

其极点分布及阶跃响应曲线如图3.4.2（a）所示，系统为无阻尼等幅振荡，振荡频率为ωn，振荡周期为。

2.欠阻尼（0＜ζ＜1）二阶系统的单位阶跃响应

当0＜ζ＜1时，二阶系统特征方程的两个根（闭环极点）为一对具有负实部的共轭复根。即

由上式可知，当0＜ζ＜1时，二阶系统的单位阶跃响应是以ωd为角频率的衰减振荡，其极点分布及阶跃响应曲线如图3.4.2（b）所示，随着ζ的减小，其振荡加剧。

3.临界阻尼（ζ=1）二阶系统的单位阶跃响应(www.xing528.com)

当ζ=1时，称为临界阻尼。此时，二阶系统的特征方程具有两个相等的负实根。即

此时，二阶系统的单位阶跃响应为

进行拉氏反变换得

其极点分布及阶跃响应曲线如图3.4.2（c）所示。

4.过阻尼（ζ＞1）二阶系统的单位阶跃响应

当ζ＞1时，二阶系统的特征方程有两个不相等的负实根，即

此时，二阶系统的单位阶跃响应为

进行拉氏反变换得

其极点分布及阶跃响应曲线如图3.4.2（d）所示，系统没有超调，且过渡时间较长。

图3.4.2　不同阻尼情况下典型二阶系统的极点分布与单位阶跃响应

通过对四种阻尼情况下二阶系统阶跃响应的分析，我们可以归纳出二阶系统自由响应的特点如下：

（1）过阻尼时，系统有两个实数极点-σ1和-σ2，对应的自由响应是两个随时间变化的指数函数，即

（2）欠阻尼时，系统有一对具有负实部的共轭复根-σd±jωd，对应的自由响应是以ωd为角频率的衰减振荡，包络线是一个指数函数，其时间常数取决于根的实部-σd。

（3）无阻尼时，系统有一对纯虚根±jωn，系统的自由响应为无阻尼等幅振荡，振荡频率是系统的无阻尼自然振荡频率。

（4）临界阻尼时，系统有一对重根-σ1，系统的自由响应中，其中一项是指数函数，另一项是时间t与指数函数的乘积。即

当ωn=3时，图3.4.3显示了ζ=0（无阻尼）、ζ=0.3（欠阻尼）、ζ=1（临界阻尼）、ζ=1.5（过阻尼）四种情况下的典型二阶系统的单位阶跃响应的形态，清楚地展现了不同阻尼情况下典型二阶系统动态过程的不同。

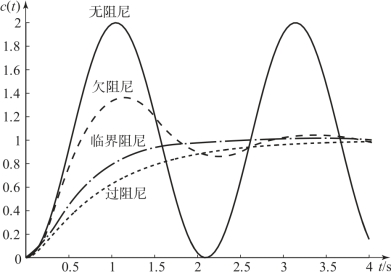
图3.4.3　不同阻尼情况下典型二阶系统的单位阶跃响应