一阶系统的时域分析技巧

一阶无零点系统的传递函数为

系统零极点示于图3.3.1。

当输入信号r（t）=1（t）时，R（s）=，系统单位阶跃响应的像函数为

图3.3.1　一阶系统的零极点图

对上式进行拉氏反变换，得系统单位阶跃响应

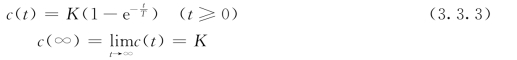
根据式（3.3.3）绘出一阶系统的单位阶跃响应曲线如图3.3.2所示，曲线在原点的斜率为1/T。

我们称T为一阶系统的时间常数，由图3.3.2可见，时间常数T是一阶系统的阶跃响应上升到其终值的63%时的时间。时间常数T反映系统的惯性，一阶系统的惯性越小，其动态响应过程越快；反之，惯性越大，动态响应越慢。

下面我们给出一阶系统的动态性能指标。(www.xing528.com)

一阶系统的上升时间定义为系统阶跃响应从其终值的10%上升到终值的90%所需要的时间，记为tr。分别令式（3.3.3）中的c（t）=0.9和c（t）=0.1，解得的两个时间之差就是上升时间，即

一阶系统极点分布与单位阶跃响应的关系动画

一阶系统的调节时间定义为系统阶跃响应到达并保持在终值的±5%（或±2%）内所需的时间，记为ts。令式（3.3.3）中的c（t）=0.95，可得

令式（3.3.3）中的c（t）=0.98，可得

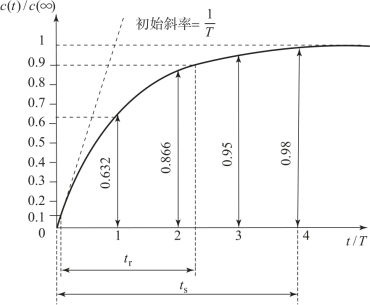
图3.3.2　一阶系统的单位阶跃响应曲线及性能指标定义

一阶系统的过渡过程时间比例于其时间常数T，即T越小，过渡过程时间越短。对照图3.3.2可知，这一特性反映在零极点图上就是一阶系统的闭环极点离虚轴越远，其过渡过程时间越短。

一阶系统有两个特征参数K和T，如果测量出其单位阶跃响应，可通过曲线来确定K和T值，确定方法是：K=c（∞），T等于c（t）=0.632c（∞）处的横坐标值。也可根据其初始斜率特性，确定一阶系统的时间常数。