极点和零点对系统输出的影响

如图3.2.1（a）所示为一个一阶系统的传递函数，其零点为-3，极点为-5，其零极点分布图如图3.2.1（b）所示。为了说明零点和极点的性质，我们来求该系统的单位阶跃响应。将图3.2.1（a）的传递函数乘上阶跃函数得

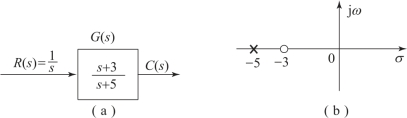
图3.2.1　一个一阶系统的传递函数及零极点分布图

（a）一阶系统传递函数；（b）零极点分布图

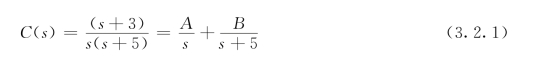
其中，C（s）中输入信号的极点是s=0，系统传递函数的极点是s=-5。因为

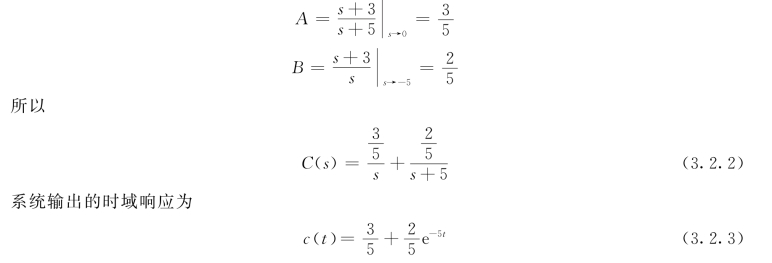
式（3.2.3）右边第一项称为受迫响应，其模态取决于输入函数的极点，是由输入量直接产生的“强迫运动”，也可以说它是由输入量“传递”过来的运动，或者说是受输入量直接“控制”的运动；第二项称为自由响应，其模态取决于系统传递函数的极点。可以看出：(www.xing528.com)

（1）输入信号函数的极点决定了受迫响应的模态（即位于原点的极点在输出中产生了一个阶跃函数）。

（2）传递函数的极点决定了自由响应的模态（即位于-5的极点产生了e-5t的运动）。

（3）实轴上的极点产生的自由响应模态是指数响应e-αt，-α是实轴上极点的位置。极点在负实轴上的位置离原点越远，对应的指数瞬态响应衰减的速度越快。

（4）所有极点和零点同时决定了受迫响应和自由响应的幅值大小（即留数A和B）。

下面通过一个例子来演示说明如何利用极点得到系统的输出响应形式，我们仅仅通过观察就能写出系统输出响应的表达式。在实轴上的每个系统传递函数极点都产生一个指数响应，它们都是自由响应的组成部分；输入信号的极点产生受迫响应的模态。

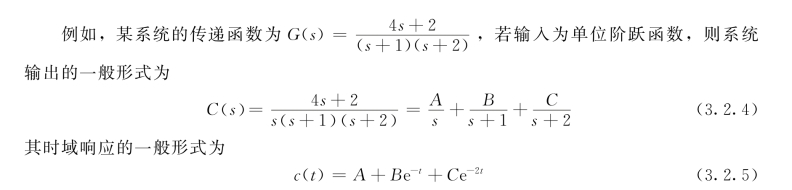
式（3.2.5）中的第一项为受迫响应，后面两项为自由响应。