系统对参数变化的灵敏度优化方案

在控制系统设计过程中，工程师应该考虑系统参数变化多少，就足以影响一个系统的性能。理想情况是系统参数的变化不明显地影响系统的性能。参数变化引起的系统传递函数的变化程度（即系统性能的变化程度），称为灵敏度。理想系统的灵敏度应为零，即系统参数变化对系统的传递函数没有任何影响。灵敏度越大，系统参数变化对系统性能的影响越大。

例如，假设函数F=K/（K+a），若K=10、a=100，则F=0.091，若a变化到原来的3倍，即a=300，则F=0.032。a的变化是（300-100）/100=2（变化了200%），而函数F =0.091，F 的变化是（0.032-0.091）/0.091=-0.65（变化了-65%），因此函数F降低了对参数a变化的灵敏度。根据前面的讨论，给出灵敏度的定义为：灵敏度是当参数的变化率接近于零时，函数变化率与参数变化率之比。即：

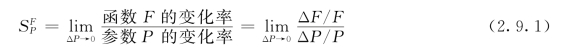
其中，P是函数F的某个参数，取微小增量的极限形式，则上式变成

控制系统对参数变化的灵敏度是重要的系统特性。

【例2.9.1】系统如图2.9.1所示，计算闭环传递函数对参数a变化的灵敏度，进一步，怎样减少该灵敏度？

(www.xing528.com)

图2.9.1　例2.9.1的反馈控制系统

【解】系统闭环传递函数为

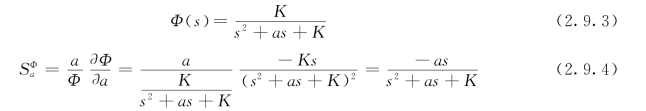
上式还是s的函数。但是，无论s的值是多少，增大K都能降低闭环传递函数对参数a变化的灵敏度。

若断开反馈回路，系统开环传递函数为

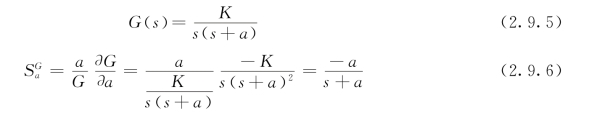
当频率较低时，开环传递函数对参数a变化的灵敏度接近于1。

可见，控制系统引入反馈后能减小参数变化对系统性能的影响，降低系统对参数变化的灵敏度，这是反馈控制系统的一个重要优点。