典型反馈控制系统的传递函数优化

经过结构图等效变换之后，反馈控制系统的典型结构图通常可以表示为如图2.8.1所示的形式。图中，Gp（s）为被控对象，Gc（s）为控制器，H（s）为测量装置。R（s）和D（s）、V（s）都是施加于系统的外作用，R（s）是有用输入，D（s）是扰动，V（s）是测量噪声，C（s）是系统的输出信号。

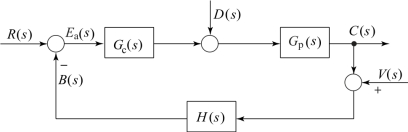
图2.8.1　反馈控制系统的典型结构图

1.开环传递函数

开环传递函数是当主反馈断开、且系统初始条件为零时，主反馈量的拉氏变换与输入量的拉氏变换之比。若以G（s）表示开环传递函数，则有

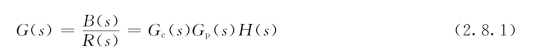
式中，Gc（s）Gp（s）称为前向通路传递函数，H（s）称为反馈通路传递函数。

2.R（s）到C（s）的闭环传递函数

令D（s）=0、V（s）=0，可求出系统输入信号R（s）到输出信号C（s）的闭环传递函数为

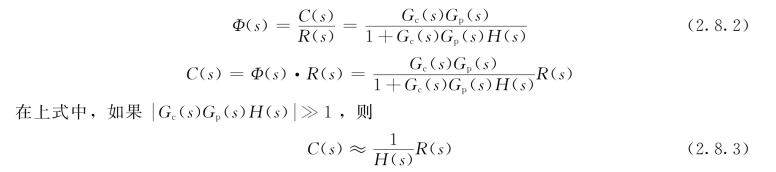
式（2.8.3）表明，在一定条件下，系统在R（s）作用下的输出只取决于反馈通路传递函数H（s），与前向通路传递函数无关。特别是当H（s）=1，即单位反馈时，C（s）≈R（s），表明系统能够近似实现对输入信号的完全复现。

3.扰动D（s）到C（s）的闭环传递函数

令R（s）=0、V（s）=0，将图2.8.1改画为图2.8.2的系统结构图后，可求出系统扰动作用D（s）到输出信号C（s）之间的闭环传递函数为(www.xing528.com)

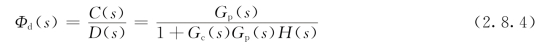
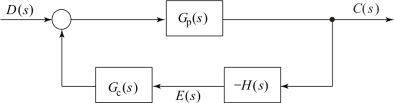
图2.8.2　在扰动作用下系统结构图

从式（2.8.4）可以看出，开环传递函数Gc（s）Gp（s）H（s）越大，干扰信号D（s）对系统输出的影响越小，即系统抑制干扰信号的能力越强。也就是说，为了获得良好的干扰信号抑制能力，在干扰信号的频率范围内，必须使开环传递函数Gc（s）Gp（s）H（s）保持较大的幅值。实际上，干扰信号一般处于低频段，因此开环传递函数在低频段应保持较大的幅值。

许多控制系统中都存在强烈的干扰信号，导致系统不能够产生精确的输出响应，例如，雷达天线的阵风干扰等。在控制系统中引入反馈，能够有效降低这些干扰对系统性能的影响。

4.噪声V（s）到C（s）的闭环传递函数

令R（s）=0、D（s）=0，可以得到系统测量噪声V（s）到系统输出C（s）的闭环传递函数为

由上式可见，当减小开环传递函数Gc（s）Gp（s）H（s）的增益时，测量噪声V（s）对系统输出的影响也随之降低，即开环传递函数Gc（s）Gp（s）H（s）越小，系统衰减测量噪声的能力就越强。更精确的说法是，为了有效地衰减测量噪声，在噪声信号的频段内，必须使开环传递函数保持较小的幅值。实际上，测量噪声信号一般都处于高频段，因此应该使开环传递函数在高频段保持较小的幅值。对于控制工程师而言，能够按照频率的高低将测量噪声和干扰信号区别开来，这是非常幸运的。这样就为一个看似两难的问题提供了解决的途径，即在选择设计控制器时，应该使系统开环传递函数在低频段的幅值较大，而在高频段的幅值较小。需要注意的是，实际系统中，有时候也会存在噪声和干扰信号的频段比较接近而难以区分的困难情况。

最后需要指出的是，对于图2.8.1典型反馈系统，其各种闭环系统传递函数的分母多项式均相同，这是因为它们都是同一信号流图的特征式，即

式（2.8.6）称为闭环系统的特征方程。