结构图等效变换优化方法

图2.6.4给出了π型滤波器的结构图，如果欲求电压U3（s）对U1（s）的传递函数，就需要进行结构图的等效变换。下面介绍结构图的等效变换法则。

1.串联结构图的等效变换

n个方框串联连接的等效方框，等于各个方框传递函数之乘积，图2.6.5表示出其变换前后的图形，则系统传递函数为

2.并联结构图的等效变换

n个方框并联连接的等效方框，等于各个方框传递函数之代数和，图2.6.6表示出其变换前后的图形，则系统传递函数为

图2.6.5　串联方框图的简化

图2.6.6　并联方框图的简化

3.比较点移动法则

图2.6.7示出了比较点后移情况，由于在比较点移至G（s）之后，输入量X2（s）不再通过G（s），因此在X2（s）与比较点之间应串入传递函数G（s）。图2.6.8示出了比较点前移情况，由于信号X2（s）到达X3（s）处时，多通过一个传递函数G（s），故在X2（s）与比较点之间应串入传递函数1/G（s）。

图2.6.7　比较点后移情况

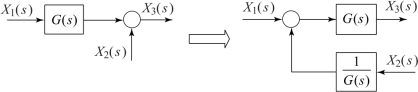
图2.6.8　比较点前移情况

4.引出点移动法则

图2.6.9示出了引出点后移情况，该图有一个输入量X1（s），有两个输出量，即X2（s）和X3（s），其中X2（s）=X1（s），若将X2（s）改由X3（s）处引出，并保持X2（s）与变换前相等，则应在X3（s）和X2（s）之间接入传递函数1/G（s）。图2.6.10示出了引出点前移情况。

图2.6.9　引出点后移情况

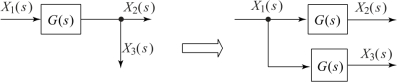
图2.6.10　引出点前移情况

5.消去反馈法则

反馈系统的结构图等效变换示于图2.6.11中，根据传递函数定义有

(www.xing528.com)

图2.6.11　消去反馈的结构图等效变化

对于负反馈情况，有

将式（2.6.6）和式（2.6.8）代入式（2.6.7）中，有

同理，对于正反馈情况，有

如果以Φ（s）表示闭环传递函数，则有

式中，“+”号对应负反馈情况，“-”号对应正反馈情况。最后强调一点，结构图等效变换的重点在于等效，即变换前输入量与输出量之间的传递函数应保持不变。

【例2.6.2】试利用结构图等效变换法则求图2.6.4中U3（s）对U1（s）的传递函数。

【解】分别应用结构图等效变换法对图2.6.4进行等效变换，其过程如图2.6.12所示。

图2.6.12　例2.6.2系统结构图简化

最后得π型滤波器的传递函数为

【例2.6.3】试利用结构图等效变换法则求图2.6.13中C（s）对R（s）的传递函数。

【解】该系统结构图的化简过程如图2.6.14所示。

先把由G1和G3组成的反馈回路进行等效变换，得到图2.6.14（b），注意这是一个正反馈回路；然后将G2前的引出点进行后移，由图2.6.14（c）可以得到系统总的传递函数为：

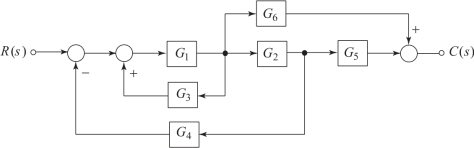
图2.6.13　系统结构图

图2.6.14　结构图化简过程