任何复杂的线性定常连续系统的传递函数均可分解成一系列基本因子的乘积,即在控制理论中,一切系统的传递函数都可认为是若干基本单元构成的“组合”,把基本单元的性质研究清楚,是研究复杂系统运动的基础。
1.比例环节G(s)=K
比例环节的输入量与输出量之间的时域关系可表示为
![]()
其传递函数为
![]()
例如,图2.5.1所示的运算放大器,其中ui(t)为输入电压,uo(t)为输出电压,R1、R2为电阻,因为
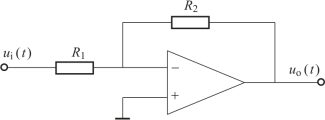
图2.5.1 运算放大器
![]()
所以运算放大器的传递函数为
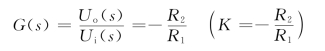
再如图2.5.2所示齿轮传动副,其中ni(t)为输入轴转速,no(t)为输出轴转速,z1、z2为齿轮齿数,因为
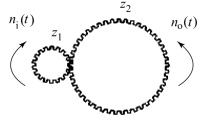
图2.5.2 齿轮传动副
![]()
则齿轮传动副的传递函数为
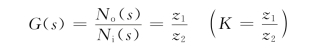
比例环节的实例还有测速电机、电位器、杠杆等。
2.一阶惯性环节G(s)=1/(Ts+1)
惯性环节的输入量与输出量之间的关系可表达为如下一阶微分方程
![]()
惯性环节的响应特点是输出量迟缓地反应输入量的变化。
惯性环节的传递函数为:
![]()
例如,如图2.5.3所示无源滤波电路,其中ui(t)为输入电压,uo(t)为输出电压,R为电阻,C为电容,因为
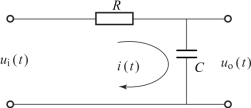
图2.5.3 无源滤波电路
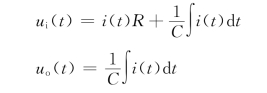
则其传递函数为
![]()
如图2.5.4所示的弹簧-阻尼器系统,其中xi(t)为输入位移,xo(t)为输出位移,k为弹簧刚度,B为阻尼系数,因为

则其传递函数为
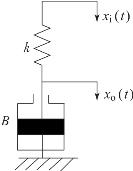
图2.5.4 弹簧-阻尼系统
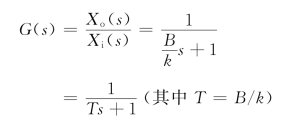
3.理想微分环节G(s)=Ks
微分环节的输出变量正比于输入变量的微分,即
![]()
微分环节的输出能预测输入信号的变化趋势。
微分环节的传递函数为
![]()
如图2.5.5所示永磁式直流测速机,其中θi(t)为输入转角,uo(t)为输出电压,因为
![]()
则
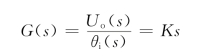
实际上,理想微分环节是难以实现的,常用的是如图2.5.6所示的近似微分环节。
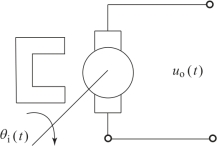
图2.5.5 永磁式直流测速机
 (https://www.xing528.com)
(https://www.xing528.com)
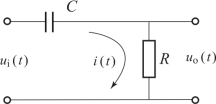
图2.5.6 无源微分网络
在图2.5.6中,R为电阻,C为电容,ui(t)为输入电压,uo(t)为输出电压,因为
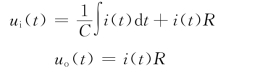
则其传递函数为
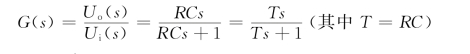
4.积分环节G(s)=K/s
积分环节的输出量正比于输入变量的积分,即
![]()
积分环节的传递函数为
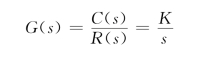
如图2.5.7所示有源积分网络,其中ui(t)为输入电压,uo(t)为输出电压,R为电阻,C为电容,因为
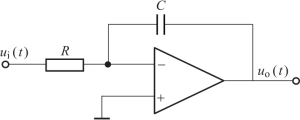
图2.5.7 有源积分网络
![]()
则其传递函数为
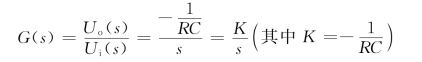
水箱的水位与进水量、电动机的角位移与转速等之间的关系都是积分关系。
5.二阶振荡环节G(s)=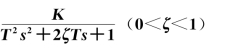
二阶振荡环节可表达为如下二阶微分方程
![]()
则其传递函数为
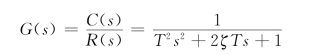
在零初始条件下,对式(2.2.5)进行拉氏变换,可得无源RLC网络的传递函数为
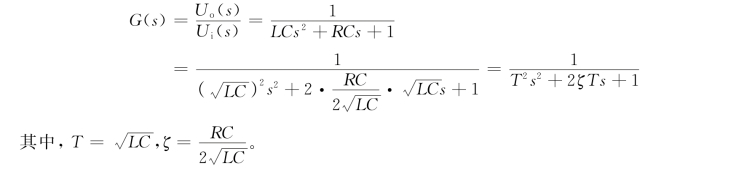
在零初始条件下,对式(2.2.8)进行拉氏变换,可得质量块-弹簧-阻尼器系统的传递函数为:
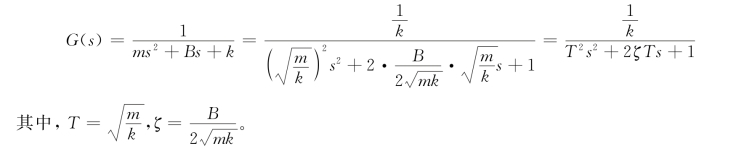
同一物理系统可以有不同形式的数学模型,而不同类型的系统也可以有相同形式的数学模型。我们称具有相同数学模型的不同物理系统为相似系统。外力引起的系统运动与外电压引起的系统运动这一相似系统,又可称为力-电压相似系统。在相似系统中占据相似位置的物理量称为相似量。数学模型对系统的研究提供了有效的数学工具,相似系统揭示了不同物理现象之间的相似关系。利用相似关系的概念,可以用一个易于实现的系统来研究与其相似的复杂系统,根据相似系统的理论出现了仿真研究法。
6.延时环节
延时环节的运动特性是输出量c(t)完全复现输入量r(t),但比输入量r(t)滞后一个固定的时间τ,即
![]()
其时间变化曲线如图2.5.8所示。
例如在图1.3.6中,由于输热管的存在,加热器给出的热量要延迟一段时间才能到达房间。
延时环节的传递函数为
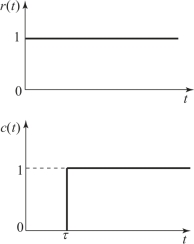
图2.5.8 延时环节的时间变化示意图
![]()
大多数分析工具都假定系统的传递函数是s的有理函数,但e-τs不是s的有理函数,如果能够用有理函数来近似延时环节,将会使分析得以简化。近似方法有以下三种。
方法1:根据指数函数的性质,有
![]()
因此可以认为
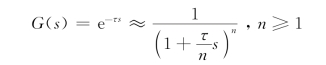
即用多个串联的惯性环节代替延时环节,而这些惯性环节的时间常数的总和等于延时环节的延时量。所用惯性环节的数量越多,则这种近似方法的精度越高,但近似公式越复杂。
方法2:把式e-τs展开为泰勒级数
![]()
由此就能看出延时环节的输出量是输入量的各阶导数。如果输入量的变化相当缓慢,就可以略去其高阶导数项,而取
![]()
甚至取
![]()
这种方法比较简便,但如果输入量函数含有迅速变化的成分(例如阶跃函数或快速的振荡),则精度较差。
方法3:帕德(Pade)近似利用超越函数e-τs的幂级数展开式,指定了一个给定阶次的待定有理函数来近似e-τs,并使该有理函数的幂级数展开式的系数与e-τs的幂级数展开式的系数尽可能多地匹配。e-τs的Pade一阶近似如下:
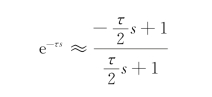
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




