控制理论中的传递函数：超前网络的传递函数求解

控制系统的微分方程是在时间域描述系统动态性能的数学模型，在给定外作用及初始条件下，求解微分方程可以得到系统的输出响应。这种方法比较直观，特别是借助于计算机可以迅速而准确地求得结果。但是当系统的结构改变或者某个参数变化时，就要重新列写并求解微分方程，不便于对系统进行分析和设计。

传递函数是经典控制理论中最重要的数学模型。在以后的分析中我们可以看到，利用传递函数不必求解微分方程，就可以研究初始条件为零的系统在输入信号作用下的动态过程；利用传递函数还可以研究系统参数变化或结构变化对动态过程的影响，使分析系统的问题大为简化。另外，还可以把对系统性能的要求转化为对系统传递函数的要求，使综合设计易于实现。

1.传递函数的定义

线性定常系统的传递函数，定义为在零初始条件下，系统输出量的拉氏变换与输入量的拉氏变换之比。

设线性定常系统由下述n阶线性常微分方程描述：

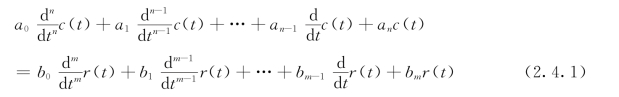
式中，c（t）是系统输出量；r（t）是系统输入量；ai（i=1，2，…，n）和bj（j=1，2，…，m）是与系统结构、参数有关的常系数。

设r（t）和c（t）及其各阶导数在t=0-时的值均为零，即零初始条件，对上式中各项分别求拉氏变换，并令C（s）=L［c（t）］，R（s）=L［r（t）］，可得代数方程为

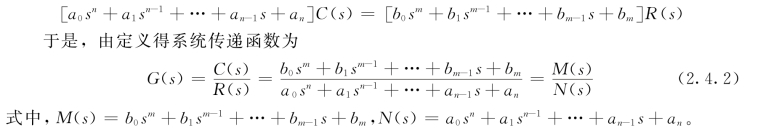
2.传递函数的性质

（1）传递函数的概念只适用于线性定常系统。

（2）传递函数是复变量s的有理真分式函数，分母多项式的最高阶次n高于或者等于分子多项式的最高阶次m，即n≥m，这是因为实际系统或者元件总是有惯性的。

（3）传递函数是一种用系统参数表示输出量与输入量之间关系的表达式，它只取决于系统的结构和参数，与输入量的形式和大小无关，也不反映系统内部的任何信息，因此可以用图2.4.1的方块图表示一个具有传递函数G（s）的线性系统。图中表明，系统输入量与输出量之间的因果关系可以用传递函数联系起来。

（4）传递函数与微分方程有相通性。传递函数分子多项式系数及分母多项式系数，分别与相应微分方程的右端及左端微分算符多项式系数相对应。故在零初始条件下，将微分方程的算符d/dt用复数s置换便得到传递函数；反之，将传递函数多项式中的变量s用算符d/dt置换便得到微分方程，即传递函数中的s与微分方程中的d/dt有相通性。

图2.4.1　传递函数的图示(www.xing528.com)

（5）传递函数G（s）的拉氏反变换是脉冲响应g（t），g（t）是系统在单位脉冲δ（t）输入时的输出响应，此时R（s）=L[δ（t）]=1，故有g（t）=L-1[C（s）]=L-1[G（s）R（s）]=L-1[G（s）]。

传递函数是在零初始状态下定义的。控制系统的零初始条件有两方面的含义：一是指输入量是在t≥0时才作用于系统，因此，在t=0-时，输入量及各阶导数均为零；二是指输入量加入系统之前，系统处于稳定的工作状态，即输出量及其各阶导数在t=0-时的值也为零，现实的工程控制系统多属于此类情况。

因此，传递函数可表征控制系统的动态性能，并用于求出在给定输入量时系统的零初始条件响应，即由拉氏变换的卷积定理，有

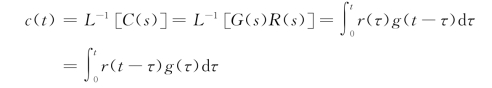
式中，g（t）=L-1［G（s）］是系统的脉冲响应。

【例2.4.1】试求如图2.4.2所示超前网络的传递函数，该电路的输入量是u1，输出量是u2。

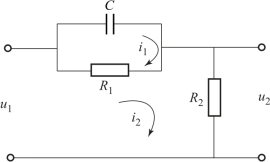
图2.4.2　超前网络电路图

【解】对电路列写回路电压方程：

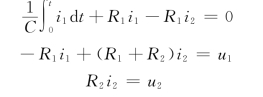
对以上三式两端取拉氏变换，并令初始条件为零，得

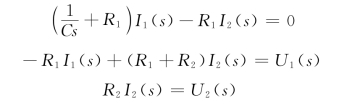
由以上三式联立，消去中间变量可得

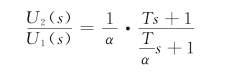
式中，T=R1C，α=（R1+R2）/R2＞1。