非线性微分方程的线性化处理

自动控制元件与系统的运动方程常常是非线性的，如例2.2.3倒立摆稳定系统的数学模型就是一组非线性微分方程。严格来讲，几乎所有实际物理系统都是非线性的，例如，弹簧的刚度与其形变有关系，因此弹簧系数k实际上是位移x（t）的函数，并非常值；电动机本身的摩擦、死区等非线性因素会使其运动方程复杂化而成为非线性方程。非线性系统的理论还不完善，且非线性系统不满足叠加性或齐次性，故用非线性微分方程研究系统的运动规律是很困难的。因此，一般我们会尽可能地对所研究的系统进行线性化处理，将非线性微分方程转化为线性微分方程，然后用线性理论进行分析。如果元件的非线性因素较弱或者不在系统线性工作范围以内，则它们对系统的影响很小，可以忽略其非线性的影响，将这些元件视为线性元件，这是通常使用的一种线性化方法。另外，还有一种线性化方法，称为切线法或者小偏差法，这种线性化方法特别适合于具有连续变化的非线性函数。

小偏差线性化的基本假设：

（1）系统中的变量在某一工作点附近做微小变化；

（2）非线性特性在该工作点可导。

在此条件下，非线性的特性曲线可用该工作点处的切线所代替，变量的增量之间满足线性函数关系。小偏差线性化的具体方法如下所述。

一般情况下，元件或系统的非线性特性如图2.3.1所示，并用如下非线性函数描述

图2.3.1　小偏差线性化示意图

其线性化的方法是，把非线性函数在工作点A附近展成泰勒级数，略去高次项，便可以得到一个以增量为变量的线性函数，即

用这个关于增量的线性方程代替关于实际变量x和y的非线性方程，可以使研究工作方便很多。小偏差线性化方法是工程上很有用的一项技巧，其实质是在一个很小的范围内，将非线性特性用一段直线来代替。由于反馈控制系统不允许出现大的偏差，因此，这种线性化方法对于研究闭环控制系统具有实际意义。

同理可得，多变量非线性函数y=f（x1，x2，…，xn）在工作点（x10，x20，…，xn0）附近的线性增量函数为

把上述线性增量函数代入微分方程，便得系统线性化的增量方程。

【例2.3.1】试将例2.2.3的倒立摆系统的运动方程线性化。(www.xing528.com)

【解】由例2.2.3可得该倒立摆系统的非线性方程组为

由于系统工作在θ0=0°附近，所以将sinθ和cosθ在θ0=0°附近进行泰勒级数展开，并略去二次方及二次方以上的项，得

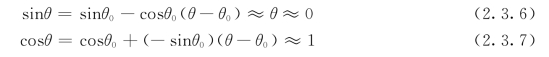
将式（2.3.6）和式（2.3.7）代入式（2.3.5）中，得

消去中间变量，得

【例2.3.2】假设一辆水平面上直线行驶的汽车的阻力主要是空气阻力，如图2.3.2所示，且其空气阻力与速度的平方成正比，是非线性的，即f（V）=bV2。

该系统的微分方程为：

图2.3.2　汽车受力分析示意图

将上述方程进行线性化，即将上式中的每一项进行线