自动控制系统微分方程描述

下面举例说明如何建立自动控制系统的微分方程。

【例2.2.1】图2.2.1是由电阻R、电感L、电容C组成的串联电路，u1（t）为输入电压，u2（t）为输出电压，试列写其运动方程。

【解】根据克希霍夫第二定律有

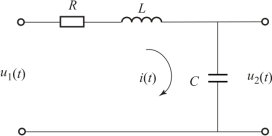
图2.2.1　RLC无源网络

【例2.2.2】图2.2.2为弹簧-质量块-阻尼器机械位移系统。试列写质量块m在外力F（t）作用下，位移x（t）的运动方程。

【解】设质量块m相对于初始状态的位移、速度、加速度分别为x（t）、d x（t）/dt、d2x（t）/dt2。由牛顿运动定律有

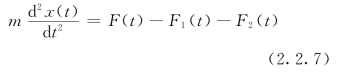
式中，F1（t）=B·d x（t）/dt是阻尼器的阻尼力，其方向与运动方向相反，其大小与运动速度成比例；B是阻尼系数。F2（t）=kx（t）是弹簧弹力，其方向也与运动方向相反，其大小与位移成比例，k是弹性系数。将F1（t）与F2（t）代入式（2.2.7）中，经整理后即得该系统的微分方程

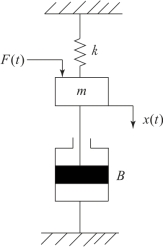
图2.2.2　弹簧-质量块-阻尼器机械位移系统

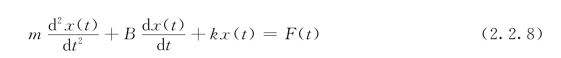
【例2.2.3】倒立摆稳定系统如图2.2.3所示，系统的组成有小车和倒摆，M为小车的质量，m为摆球的质量，l为摆长。希望在小车的推力作用下，始终保持倒摆垂直于地面，研究倒立摆稳定系统是有重要实际意义的。

为简化问题，只考虑摆在平面内的运动，并忽略空气阻力及摆杆质量。本系统的输入量是对小车的作用力f，输出量是倒摆与铅垂线的夹角θ，试列写其运动方程。

【解】摆球受力分析如图2.2.4所示，则摆球水平方向运动方程为

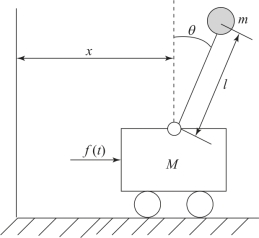
图2.2.3　倒立摆系统

(www.xing528.com)

小车受力分析如图2.2.5所示。

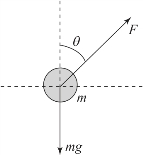
图2.2.4　摆球受力分析

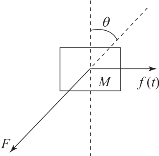
图2.2.5　小车受力分析

摆球垂直方向运动方程为

【例2.2.4】某机械转动系统如图2.2.6所示，其中J为转动惯量，B为转动轴上的黏性摩擦系数，τ（t）为外作用力矩，是系统的输入量；θ（t）为转动轴的角位移，是系统的输出量，试列写系统的微分方程。

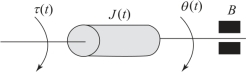
图2.2.6　机械转动系统

【解】由牛顿定律可得机械转动系统的力矩方程为：

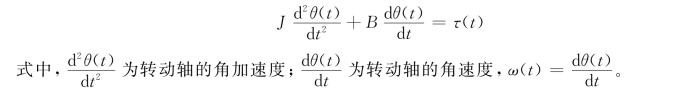
若以转动轴的角速度ω（t）作为系统的输出量，则机械转动系统的力矩微分方程为：

综上所述，列写元件微分方程的步骤可归纳如下：

（1）根据元部件的工作原理及其在控制系统中的作用，确定其输入量和输出量。

（2）分析元部件工作中所遵循的物理规律或化学规律，列写出相应的微分方程。

（3）消去中间变量，得到输入量和输出量之间的微分方程，便是元部件的微分方程数学模型。一般情况下，应将微分方程写为标准形式，即与输入量有关的项写在方程的右端，与输出量有关的项写在方程的左端，方程两端变量的导数项均按降幂排列。