自动控制系统的典型外作用分析与优化

在工程实践中，自动控制系统承受的外作用形式多种多样，对不同形式的外作用，系统被控量的变化情况（即响应）各不相同。为了便于用统一的方法研究和比较控制系统的性能，通常选用几种函数作为典型外作用，系统的性能指标一般是基于系统对典型外作用的响应而给出的。可选作典型外作用的函数应具备以下条件：

·这种函数在现场或实验室中容易得到；

·在工程中经常遇到，并且可能是最不利的外作用；

·这种函数的数学表达式简单，便于理论计算。

目前，在控制工程设计中常用的典型外作用函数有阶跃函数、斜坡函数、脉冲函数及正弦函数等。

1.阶跃函数

阶跃函数的数学表达式为

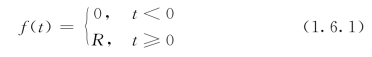
式（1.6.1）表示一个在t=0时出现的幅值为R的阶跃变化函数，如图1.6.1所示。在实际系统中，这意味着t=0时突然加到系统上的一个幅值不变的外作用。幅值R=1的阶跃函数，称为单位阶跃函数，用1（t）表示，幅值为R的阶跃函数便可表示为f（t）=R·1（t）。在任意时刻t0出现的阶跃函数可表示为f（t-t0）=R·1（t-t0）。

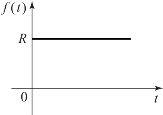
图1.6.1　阶跃函数

阶跃函数是自动控制系统在实际工作条件下经常遇到的一种外作用形式。例如，电源电压的突然跳动、负载的突然增大或减小、飞机飞行中遇到的常值阵风扰动等，都可视为阶跃函数形式的外作用。在控制系统的分析设计工作中，一般将阶跃函数作用下系统的响应特性作为评价系统动态性能的依据。

2.斜坡函数

斜坡函数的数学表达式为

式（1.6.2）表示在t=0时刻开始，以恒定速率R随时间而变化的函数，如图1.6.2所示。在工程实践中，某些随动系统就常常工作于这种外作用下，如雷达高射炮防空系统，当雷达跟踪的目标以恒定速率飞行时，便可视为该系统工作于斜坡函数作用之下。(www.xing528.com)

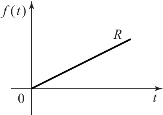
图1.6.2　斜坡函数

3.脉冲函数

脉冲函数定义为

式中，（A/t0）［1（t）-1（t-t0）］是由两个阶跃函数合成的脉动函数，其面积A=（A/t0）t0，如图1.6.3（a）所示。当宽度t0趋于零时，脉动函数的极限便是脉冲函数，它是一个宽度为零、幅值为无穷大、面积为A的极限脉冲，如图1.6.3（b）所示。脉冲函数的强度通常用其面积表示。面积A=1的脉冲函数称为单位脉冲函数或δ函数；强度为A的脉冲函数可表示为f（t）=Aδ（t）。在t0时刻出现的单位脉冲函数则表示为δ（t-t0）。

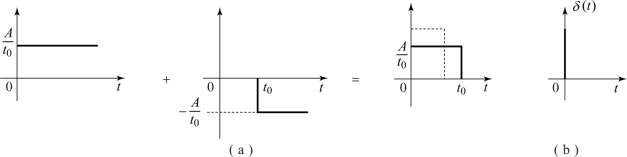
图1.6.3　脉动函数和脉冲函数

（a）两个阶跃函数合成脉动函数；（b）脉冲函数

脉冲函数在现实中是不存在的，只有数学上的定义，但它是一个重要而有效的数学工具。在自动控制理论研究中，它也具有重要作用。例如，一个任意形式的外作用，可以分解成不同时刻的一系列脉冲函数之和，这样，通过研究控制系统在脉冲函数作用下的响应特性，便可以了解系统在任意形式外作用下的响应特性。

4.正弦函数

正弦函数的数学表达式为

式中，A为正弦函数的振幅；ω为正弦函数的角频率；φ为初始相位。

正弦函数是控制系统常用的一种典型外作用，很多实际的随动系统就是经常在这种正弦函数外作用下工作的。例如舰船的消摆系统，就是处于形如正弦函数的波浪下工作的。更为重要的是，系统在正弦函数作用下的响应，即频率响应，是自动控制理论中分析与设计控制系统的重要依据（详见第5章）。