直线的投影及其特性

1.直线的投影图

空间一直线的投影可由直线上的两点（通常取线段两个端点）的同面投影来确定。如图2-18所示的直线AB，求作它的三面投影图时，可分别作出A、B两端点的投影（a、a＇、a″）、（b、b＇、b″），然后将其同面投影连接起来即得直线AB的三面投影图（ab、a＇b＇、a″b″）。

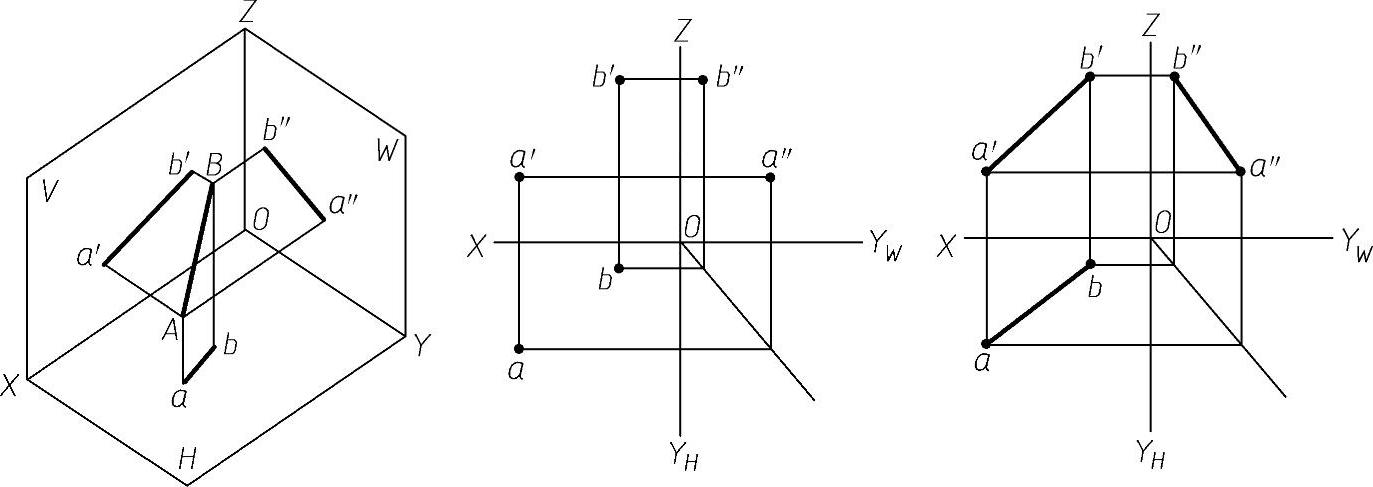
图2-18 直线的投影

2.直线对于一个投影面的投影特性

空间直线相对于一个投影面的位置有平行、垂直、倾斜三种，三种位置有不同的投影特性，如图2-19所示。

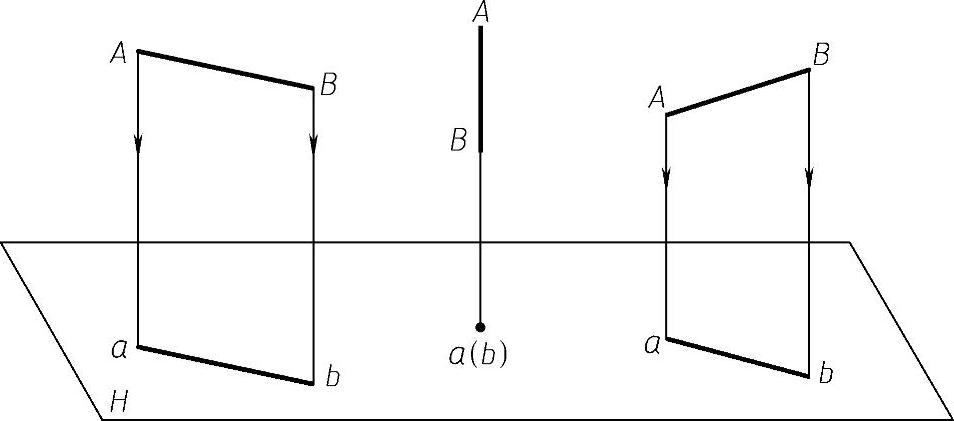
图2-19 直线的投影

1）真实性：当直线与投影面平行时，则直线的投影为实长。

2）积聚性：当直线与投影面垂直时，则直线的投影积聚为一点。

3）收缩性：当直线与投影面倾斜时，则直线的投影小于直线的实长。

根据直线在三投影面体系中的位置可分为投影面倾斜线、投影面平行线、投影面垂直线三类。前一类直线称为一般位置直线，后两类直线称为特殊位置直线。

（1）投影面平行线 平行于一个投影面且同时倾斜于另外两个投影面的直线称为投影面平行线。平行于V面的称为正平线；平行于H面的称为水平线；平行于W面的称为侧平线。

直线与投影面所夹的角称为直线对投影面的倾角。

α、β、γ分别表示直线对H面、V面、W面的倾角。

举例说明正平线的投影特性，如图2-20所示。

强调：①斜线反映实长。

②直线的倾角α、γ。

总结投影面平行线的投影特性：两平一斜。

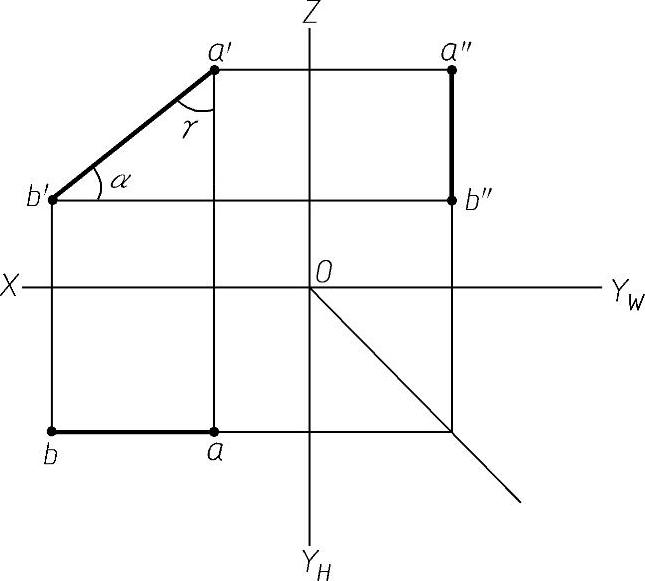
图2-20 正平线

对于投影面平行线的辨认：当直线的投影有两个平行于投影轴，第三投影与投影轴倾斜时，则该直线一定是投影面平行线，且一定平行于其投影为倾斜线的那个投影面。

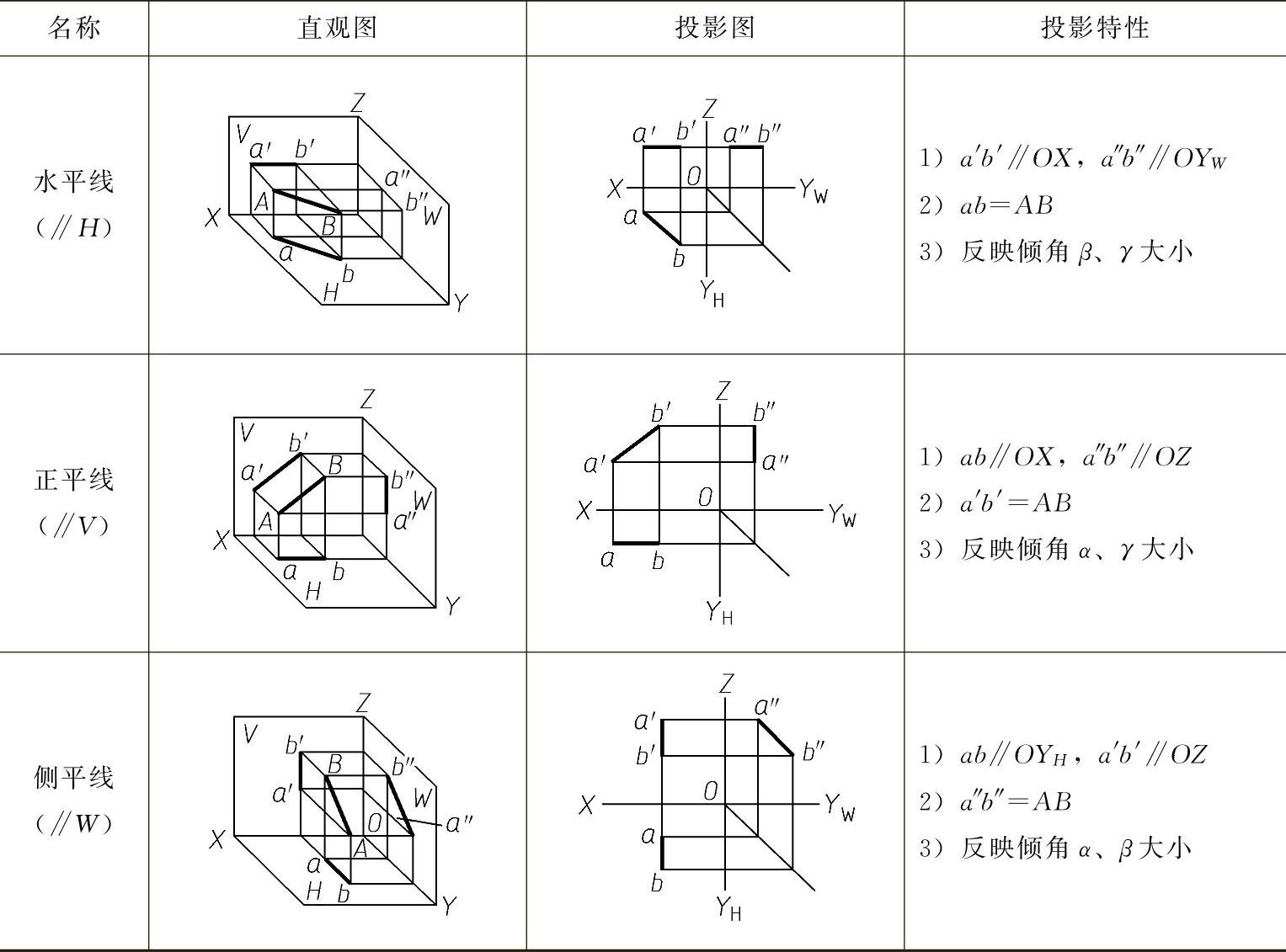
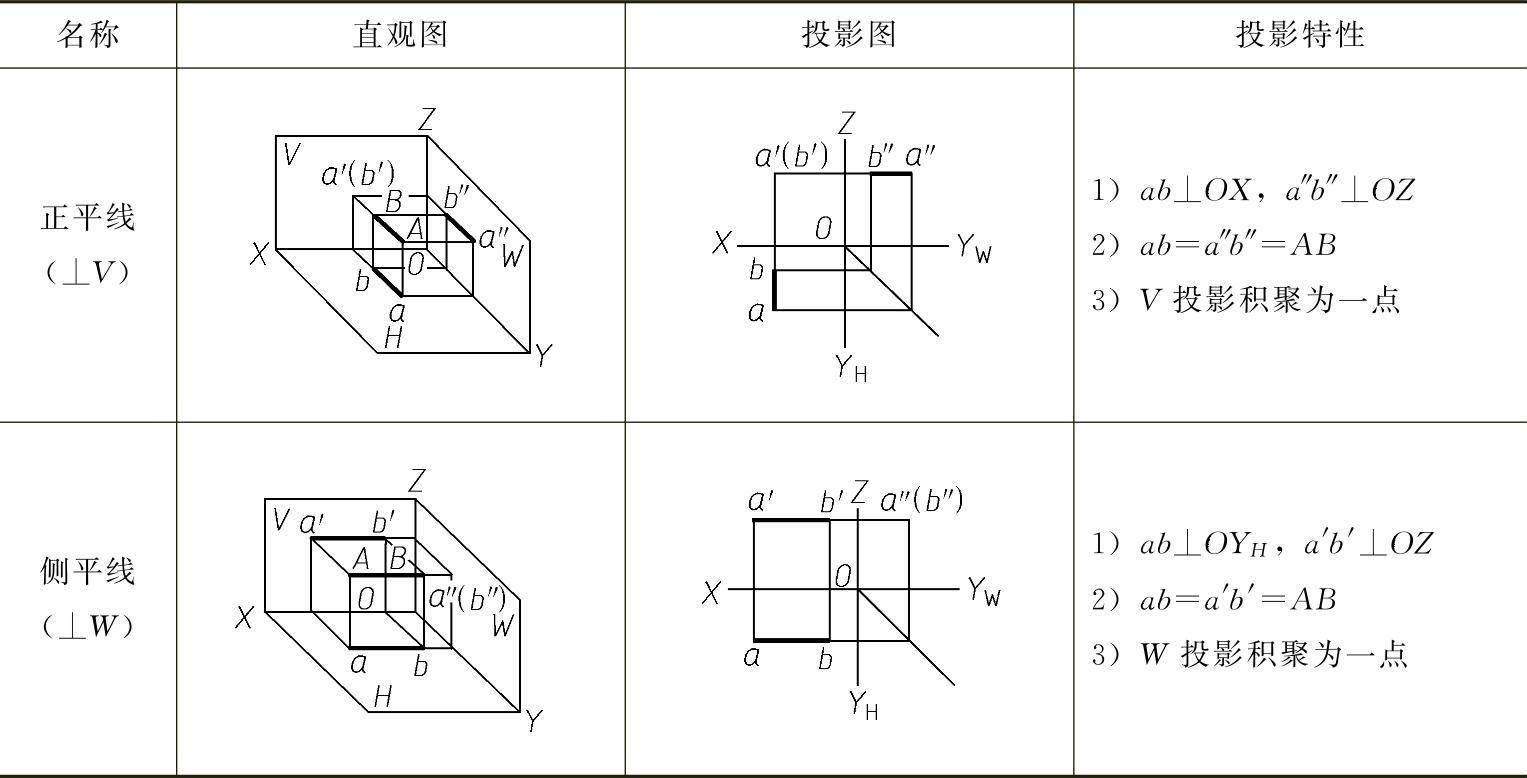
投影面平行线的投影特性见表2-1。

表2-1 投影面平行线

例题（例2-3）如图2-21a所示，已知空间点A，试作线段AB，长度为15mm，并使其平行V面，与H面倾角α=30°。

作图步骤：如图2-21b所示。

根据图为正平线，V面反映实长，H面内过a＇点作与H面夹角为30°的射线，再以a＇点量取实长15mm得点b＇，另外两投影平行于相应的投影轴，利用点的投影规律作出b、b″点。

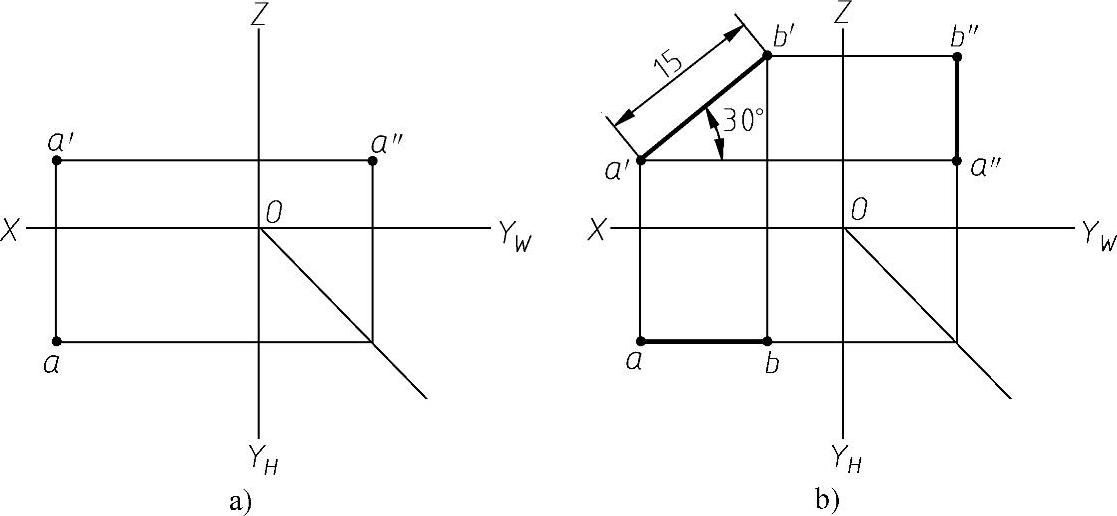
图2-21 作正平线AB

a）题目 b）解答

（2）投影面垂直线 垂直于一个投影面且同时平行于另外两个投影面的直线称为投影面垂直线。垂直于V面的称为正垂线；垂直于H面的称为铅垂线；垂直于W面的称为侧垂线。

举例说明侧垂线的投影特性：

强调：①两个投影反映实长。

②一个投影积聚为一点。

总结投影面垂直线的投影特性：两线一点。(www.xing528.com)

对于投影面垂直线的辨认：直线的投影中只要有一个投影积聚为一点，则该直线一定是投影面垂直线，且一定垂直于其投影积聚为一点的那个投影面。

投影面垂直线的投影特性见表2-2。

表2-2 投影面垂直线

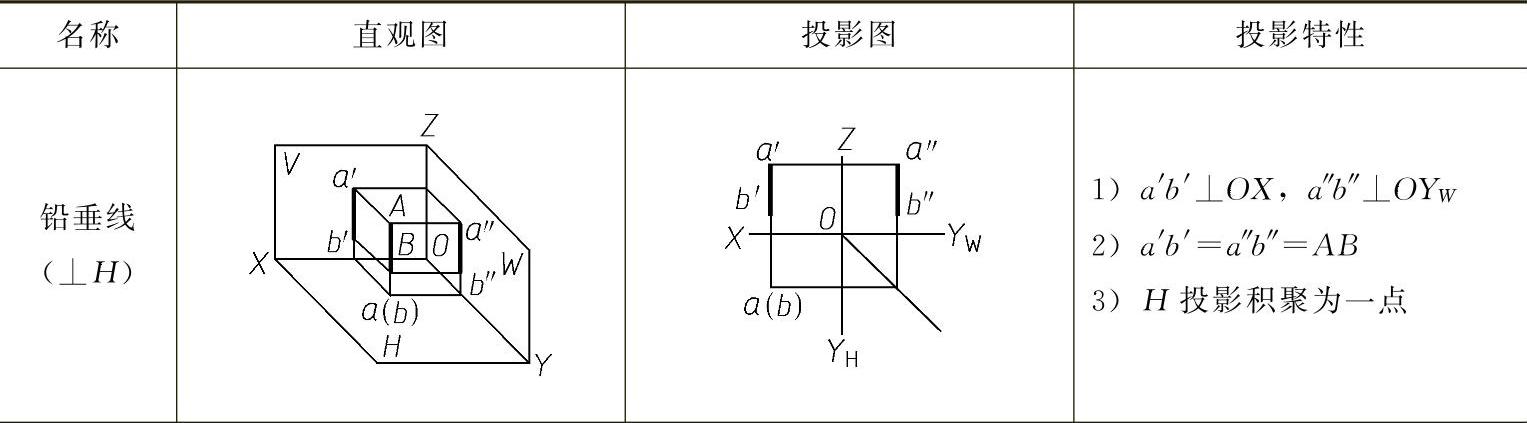
（续）

例题（例2-4）如图2-22a所示，已知正垂线AB的点A的投影，直线AB长度为10mm，试作直线AB的三面投影。

作图步骤：如图2-22b所示。

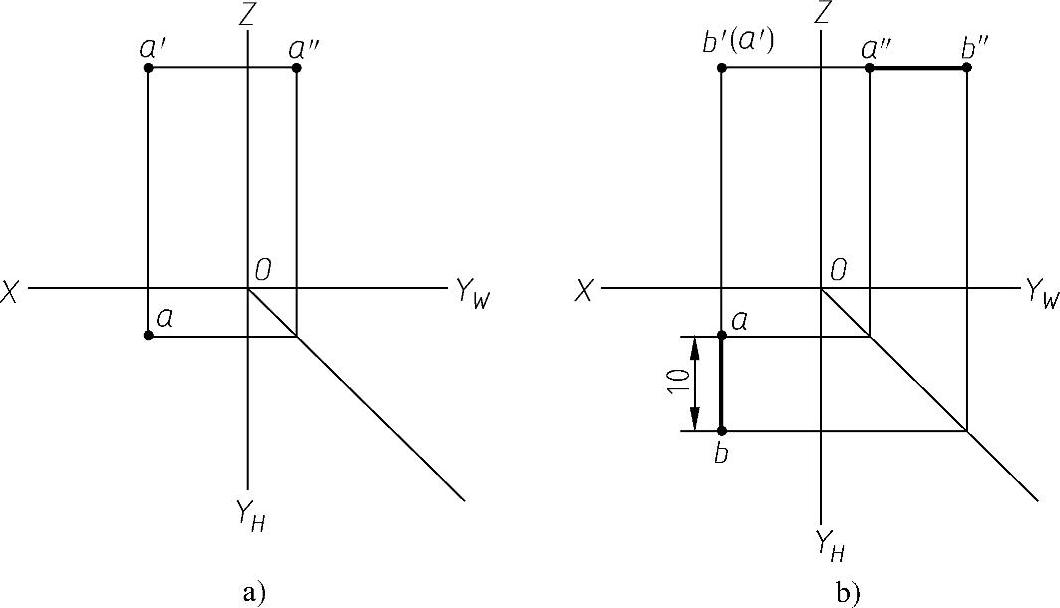
图2-22 作正垂线AB

a）题目 b）解答

根据图为正垂线，V面积聚为一点b＇（a＇），另外两投影反映实长，过a、a″点作与投影轴平行的射线，再以a、a″点量取实长10mm得点b、b″。

（3）一般位置直线 与三个投影面都处于倾斜位置的直线称为一般位置直线。

举例：如图2-23a所示，直线AB与H、V、W面都处于倾斜位置，倾角分别为α、β、γ。其投影如图2-23b所示。

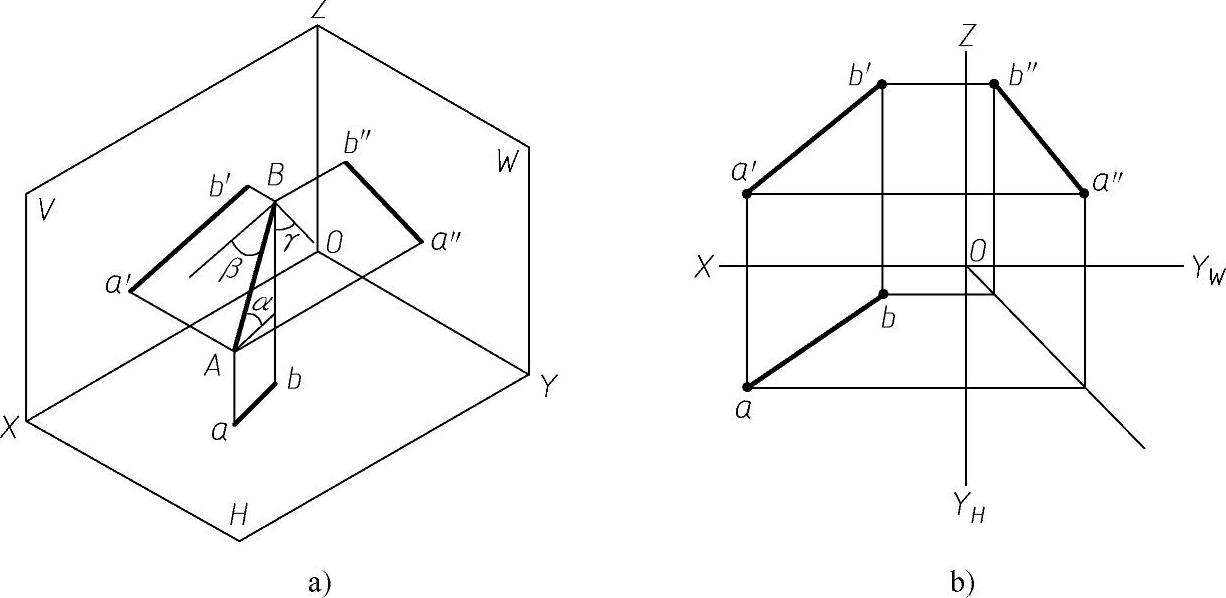
图2-23 一般位置直线

一般位置直线的投影特征可归纳如下：

1）直线的三个投影和投影轴都倾斜，各投影和投影轴所夹的角度不等于空间线段对相应投影面的倾角。

2）任何投影都小于空间线段的实长，也不能积聚为一点。

对于一般位置直线的辨认：直线的投影如果与三个投影轴都倾斜，则可判定该直线为一般位置直线。

3.一般位置直线的实长和对投影面的倾角

（1）直角三角形法的作图原理 如图2-24所示，AB为一般位置直线，过端点A作直线平行其水平投影ab并交Bb于C，得直角三角形ABC。在直角三角形ABC中，斜边AB就是线段本身，底边AC等于线段AB的水平投影ab，对边BC等于线段AB的两端点到H面的距离差（Z坐标差），也等于a＇b＇两端点到投影轴OX的距离差，而AB与底边AC的夹角即为线段AB对H面的倾角α。

（2）直角三角形法的作图方法和步骤 根据上述分析，只要用一般位置直线在某一投影面上的投影作为直角三角形的底边，用直线的两端点到该投影面的距离差为另一直角边，作出一直角三角形。此直角三角形的斜边就是空间线段的真实长度，而斜边与底边的夹角就是空间线段对该投影面的倾角。这就是直角三角形法。

作图方法与步骤如图2-25所示，用线段的任一投影为底边，均可用直角三角形法求出空间线段的实长，其长度是相同的，但所得倾角不同。

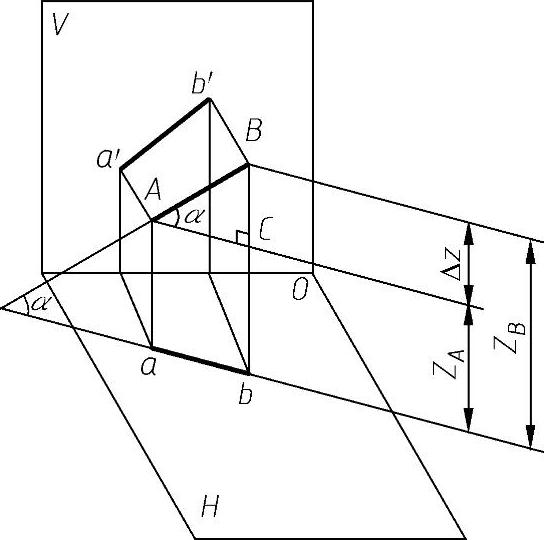
图2-24 直角三角形法的原理

在直角三角形法中，直角三角形包含四个因素：投影长、坐标差、实长、倾角。只要知道其中两个因素，就可以将其余两个求出来。

（3）例题（例2-5） 如图2-26a所示，已知直线AB的实长L=15mm，及直线AB的水平投影ab和点A的正面投影a＇，试用直角三角形法求出直线AB的正面投影a＇b＇。

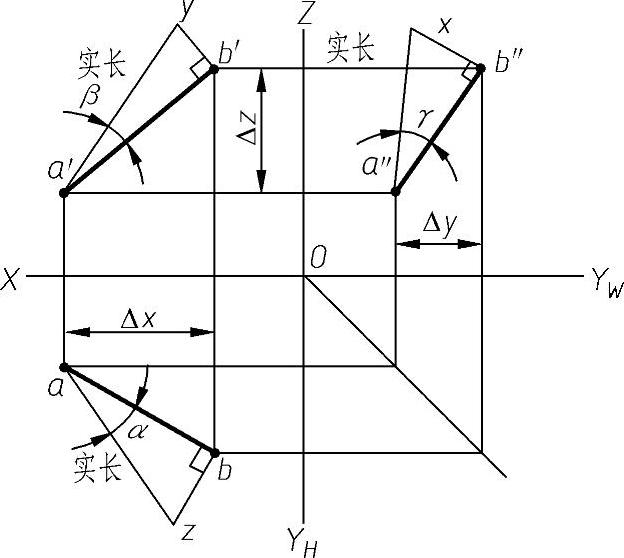
图2-25 直角三角形法

作图步骤：如图2-26b所示

如图所示的AB及ab。过A作AB_o//ab，交Bb于B_o，由正投影的特性及倾角的定义，可知△AB_oB为直角三角形，∠BAB_o=α，α角的邻边为水平线，因此AB_o平行且等于ab，α角的对边为铅垂线，所以BB_o=|Bb-Aa|=|z_B-z_A|=Δz_AB，即A、B两端点垂直方向的高差。把该直角三角形重合在H面上，用直角三角形法求一般位置直线段实长和倾角α实形的步骤可概括为：①过端点b（或a）作ab的垂线，简述为作垂线。②在另一投影图上量取高差，简述为量高差。③连斜边即为实长，斜边与投影ab的夹角即为倾角α的实形。

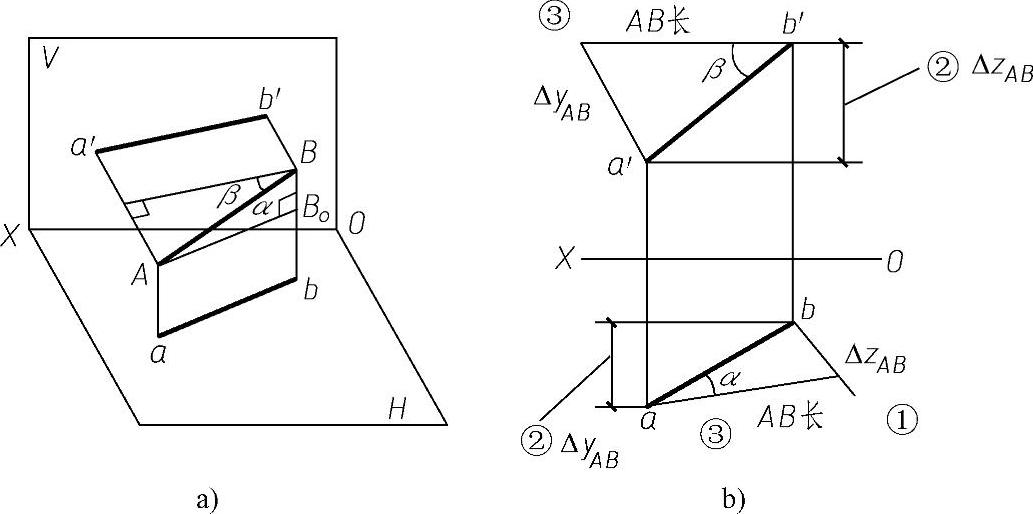
图2-26 直角三角形法应用示例

a）题目 b）解答