1.等分线段
1)过已知线段的一个端点,画任意角度的直线,并用分规自线段的起点量取n个线段。
2)将等分的最末点与已知线段的另一端点相连。
3)过各等分点作该线的平行线与已知线段相交即得到等分点,即推画平行线法。如图1-12所示。
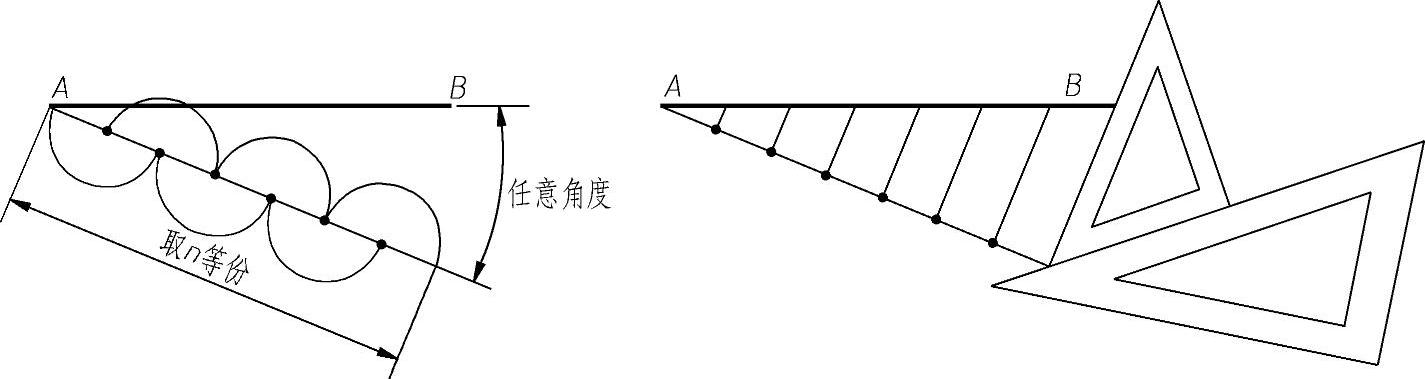
图1-12 等分直线段
2.等分圆作正多边形
(1)正五边形 方法:
1)作OA的中点M,如图1-13a所示。
2)以M点为圆心,M1为半径作弧,交水平直径于K点。如图1-13b所示。
3)以1K为边长,将圆周五等分,即可作出圆内接正五边形,如图1-13c所示。

图1-13 正五边形画法
(2)正六边形 分为用圆规作图和用三角板作图两种方法。
方法一:用圆规作图
分别以已知圆在水平直径上的两处交点A、B为圆心,以R=D/2作圆弧,与圆交于C、D、E、F点,依次连接A、B、C、D、E、F点即得圆内接正六边形,如图1-14a所示。
方法二:用三角板作图
以60°三角板配合丁字尺作平行线,画出四条斜边,再以丁字尺作上、下水平边,即得圆内接正六边形,如图1-14b所示。
(3)正n边形 以正七边形为例进行说明。
n等分铅垂直径AK(在图中n=7),以A点为圆心,AK为半径作弧,交水平中心线于点S,延长连线S2、S4、S6,与圆周交得点G、F、E,再作出它们的对称点,即可作出圆内接正n边形。

图1-14 正六边形画法

图1-15 正n边形画法
3.斜度锥度
(1)概念 斜度是指一直线(或平面)对另一直线(或平面)的倾斜程度,它的特点是单向分布。锥度是指正圆锥底圆直径与其高度之比,或正圆台的两底圆直径差与其高度之比,它的特点是双向分布。
(2)计算
斜度:高度差与长度之比。
斜度=H/L=1∶n
锥度:直径差与长度之比。
锥度=D/L=(D-d)/1=1∶n
注意:计算时,均把比例前项化为1,在图中以1∶n的形式标注。
(3)画法 如图1-16所示。

图1-16 斜度、锥度的画法
4.近似椭圆
椭圆常用画法有同心圆法和四心圆弧法两种:
(1)同心圆法 如图1-17a所示,以AB和CD为直径画同心圆,然后过圆心作一系列直径与两圆相交。由各交点分别作与长轴、短轴平行的直线,即可相应找到椭圆上各点。最后,光滑连接各点即可。
(2)椭圆的近似画法(四心圆弧法) 如图1-17b所示。
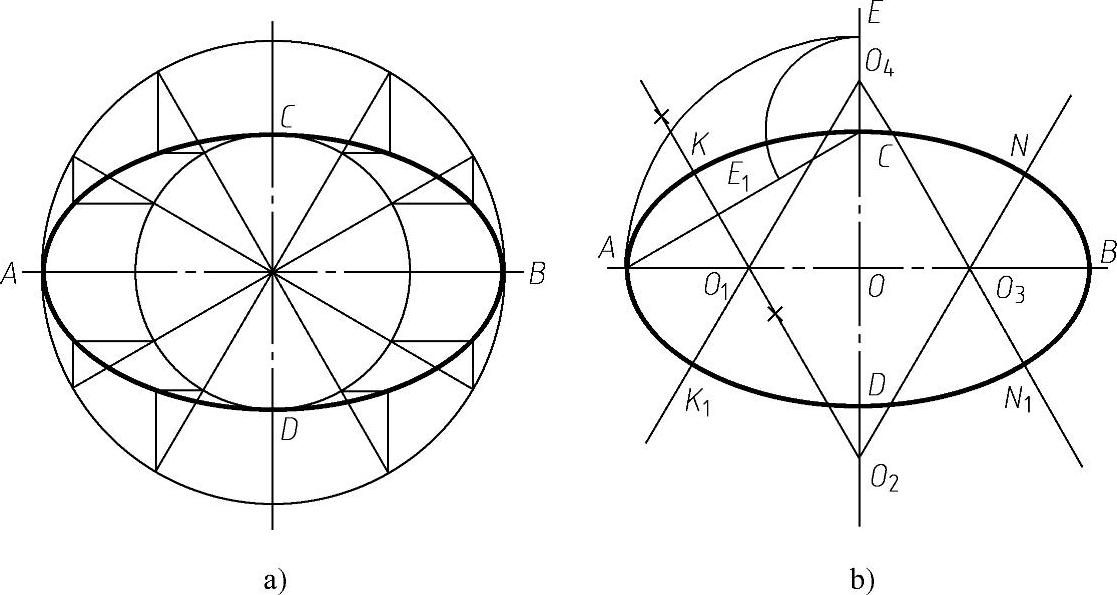
图1-17 椭圆的画法(https://www.xing528.com)
a)同心圆法 b)四心圆弧法
已知椭圆的长轴AB与短轴CD:
1)连AC,以O为圆心,OA为半径画圆弧,交CD延长线于E。
2)以C为圆心,CE为半径画圆弧,截AC于E1。
3)作AE1的中垂线,交长轴于O1,交短轴于O2,并找出O1和O2的对称点O3和O4。
4)把O1与O2、O2与O3、O3与O4、O4与O1分别连直线。
5)以O1、O3为圆心,O1A为半径;O2、O4为圆心,O2C为半径,分别画圆弧到连心线,K、K1、N1、N为连接点即可。
5.圆弧连接
(1)圆弧连接作图的基本步骤 首先求作连接圆弧的圆心,它应满足到两被连接线段的距离均为连接圆弧的半径的条件;然后找出连接点,即连接圆弧与被连接线段的切点;最后在两连接点之间画连接圆弧。
已知条件:已知连接圆弧的半径。
实质:就是使连接圆弧和被连接的直线或被连接的圆弧相切。
关键:找出连接圆弧的圆心和连接点(即切点)。
(2)直线间的圆弧连接 作图法归纳为三点:如图1-18所示。

图1-18 直线间的圆弧连接
1)定距:作与两已知直线分别相距为R(连接圆弧的半径)的平行线。两平行线的交点O即为圆心。
2)定连接点(切点):从圆心O向两已知直线作垂线,垂足即为连接点(切点)。
3)以O为圆心,以R为半径,在两连接点(切点)之间画弧。
(3)圆弧间的圆弧连接
1)连接圆弧的圆心和连接点的求法。
作图法归纳为三点(如图1-19所示):
①用算术法求圆心:根据已知圆弧的半径R和连接圆弧的半径r,计算出连接圆弧的圆心轨迹线圆弧的半径R1或R2:
外切时:R1=R+r;
内切时:R2=R-r。
②用连心线法求连接点(切点)

图1-19 算术法求圆心
外切时:连接点在已知圆弧和圆心轨迹线圆弧的圆心连线上;
内切时:连接点在已知圆弧和圆心轨迹线圆弧的圆心连线的延长线。
③以O为圆心,以r为半径,在两连接点(切点)之间画弧。
2)圆弧间的圆弧连接的两种形式。
①外连接:连接圆弧和已知圆弧的弧向相反(外切),如图1-20a所示。
②内连接:连接圆弧和已知圆弧的弧向相同(内切),如图1-20b所示。
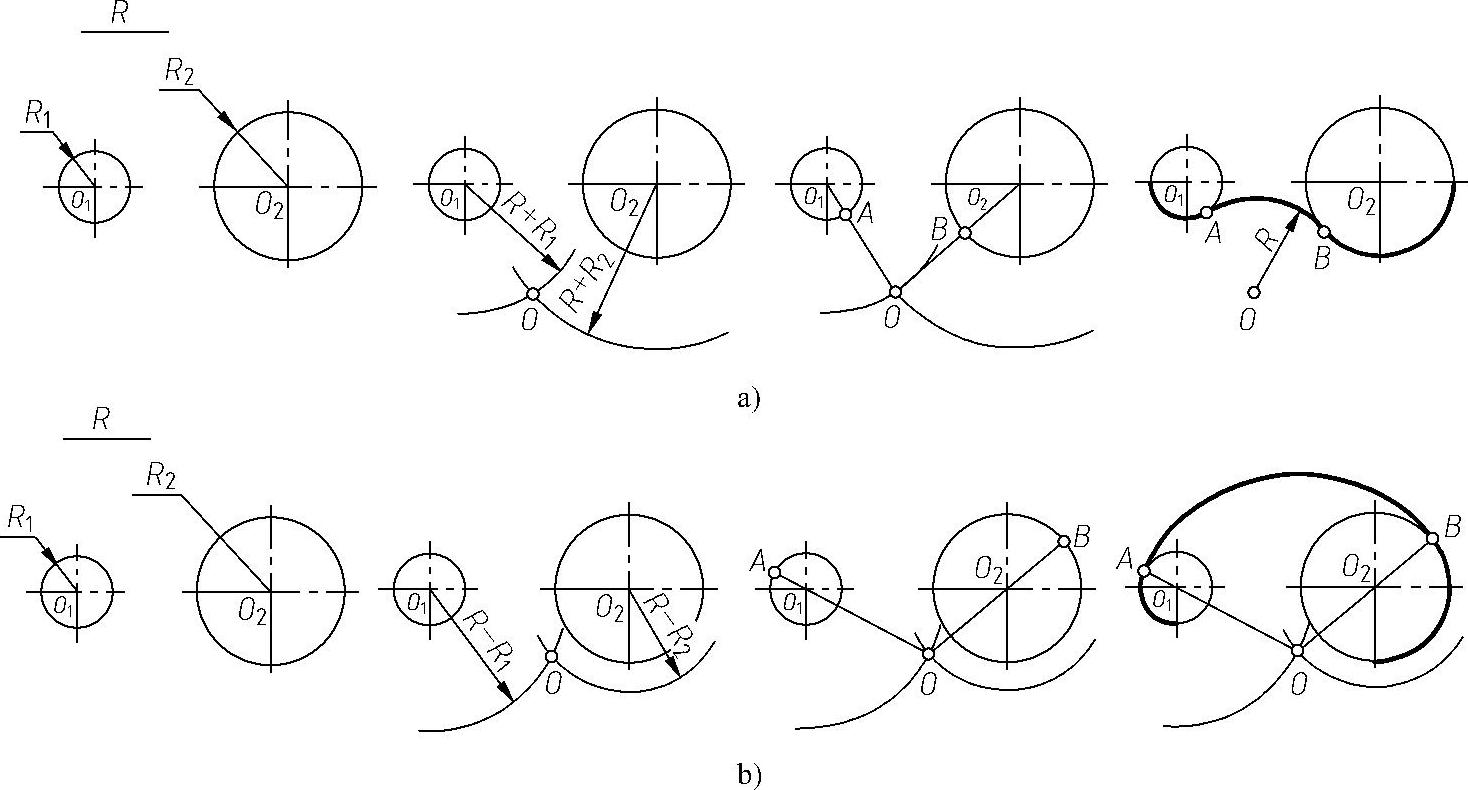
图 1-20
(4)作与已知圆相切的直线 与圆相切的直线,垂直于该圆心与切点的连线。因此,利用三角板的两直角边,便可作圆的切线,如图1-21a、b所示;作两圆的公切线如图1-21c所示。
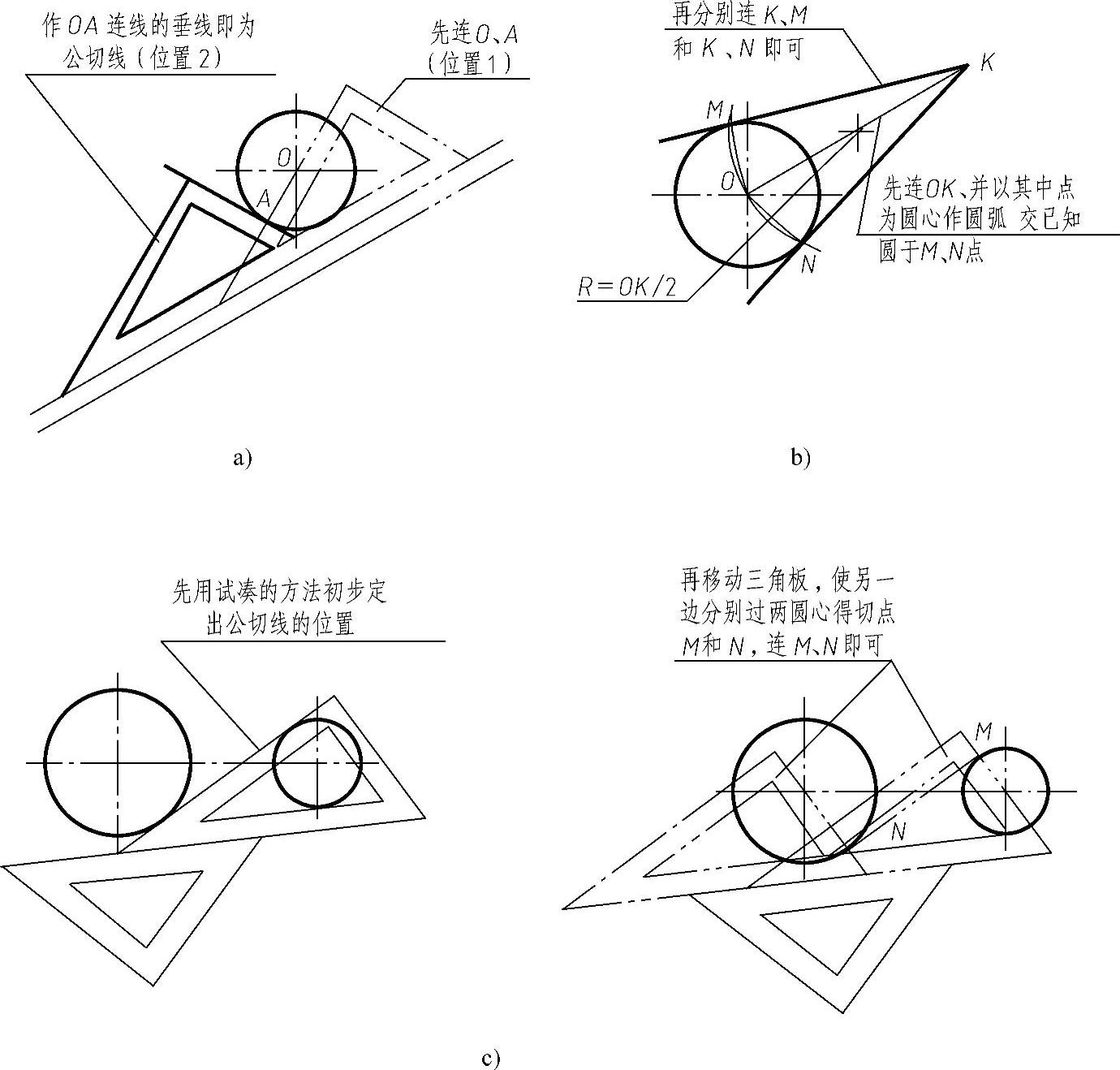
图1-21 作圆的切线

图1-22 平面图形
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




