基于磁通量离散阵列模型的金属截面积变化部位测定方法

只将拉索中出现缺陷的单股钢绞线进行替换而非整索替换，是平行钢绞线拉索换索工程中的一种新技术，可以提高换索效率、节省换索成本。在整根平行钢绞线拉索中，准确确定出现缺陷的钢绞线股，是该单股换索技术面临的难题，特别是对于在役拉索的维护而言。因此，为获取拉索较完备的状态信息，给拉索的维护提供依据及指导，除需进行金属截面积变化量测量外，有必要进行金属截面积变化部位的准确定位测量。拉索金属截面积变化的轴向定位较容易实现，而对于截面内金属变化部位的径向和周向二维量的定位测量则相对比较困难。受大直径、大提离、外层钢丝对内层钢丝的屏蔽作用等因素的影响，采用漏磁检测法很难实现对拉索缺陷的准确定位测量。因此，提出一种基于金属截面磁通量离散阵列模型的定位测量方法进行拉索金属截面积变化部位的测定方法。

通过一定的方式沿拉索周向均匀布置多个磁性传感器，金属被磁化后，当金属截面积发生变化时，则磁性传感器获取的磁信号将发生改变，不同周向位置磁性传感器的磁信号改变量将包含金属截面积变化的位置信息。不同位置的金属截面积变化将导致周向布置磁性传感器的磁信号不同，这个推断过程可以称为金属截面积变化部位测定的正演，而由周向布置磁性传感器的测量结果估算金属截面积变化的径向和周向部位的过程可被称为金属截面积变化部位反演测定。

金属截面积变化部位测定的反演问题就是进行金属截面积变化部位测定所要解决的问题，部位测定的结果就是对反演问题求解的结果，而反演问题的求解是与正演问题密切相关的。对反演问题的求解（特别是对非线性反演问题求解）实际上是在模型空间内反复进行正演迭代寻优计算。因此，欲求解反演问题，首先必须解决相应的正演问题。在金属截面积变化部位测定反演求解中同样应先建立部位测定的正演模型。反演方法的两个核心问题是找到快速、准确的正演模型和找到正演模型参数的最优化迭代方法进行反演问题的快速求解。

拉索截面内磁通量的分布情况可以反映拉索金属截面积变化的位置，但如何获取截面内磁通量的分布情况却是一件困难的事情，在不破坏拉索的情况下很难直接从拉索截面获得，必须通过其他的间接方式获取。通过设置导磁磁路将拉索截面内的磁通量导入其内，在导磁磁路中设置磁敏元件进行拉索截面内磁通量的测量。设置导磁磁路与拉索表面基本紧贴，则拉索中的磁通量几乎全部通过导磁磁路形成回路，而漏磁通量很小可以忽略不计。根据磁通量连续原理，通过导磁磁路的磁通量应等于拉索截面内的磁通量。

图6-39中导磁磁路中间部位的圆周上放置测量元件，该圆周称为测量圆Θ_m。实际测量时，m个测试点均匀地分布于测量圆Θ_m上，每个测试点的位置为G_i（i=1，2，…，m）。显然，为保证这种布置实际可行，测量圆Θ_m的半径应稍大于拉索半径R。当测试点的数量m足够大时，每个测试点所在区域的面积将非常小。当在每个测试点区域设置霍尔元件等磁敏测量元件时，磁敏元件测量的磁感应强度与该测量点所在区域的面积的乘积即为通过该测量点区域的磁通量。

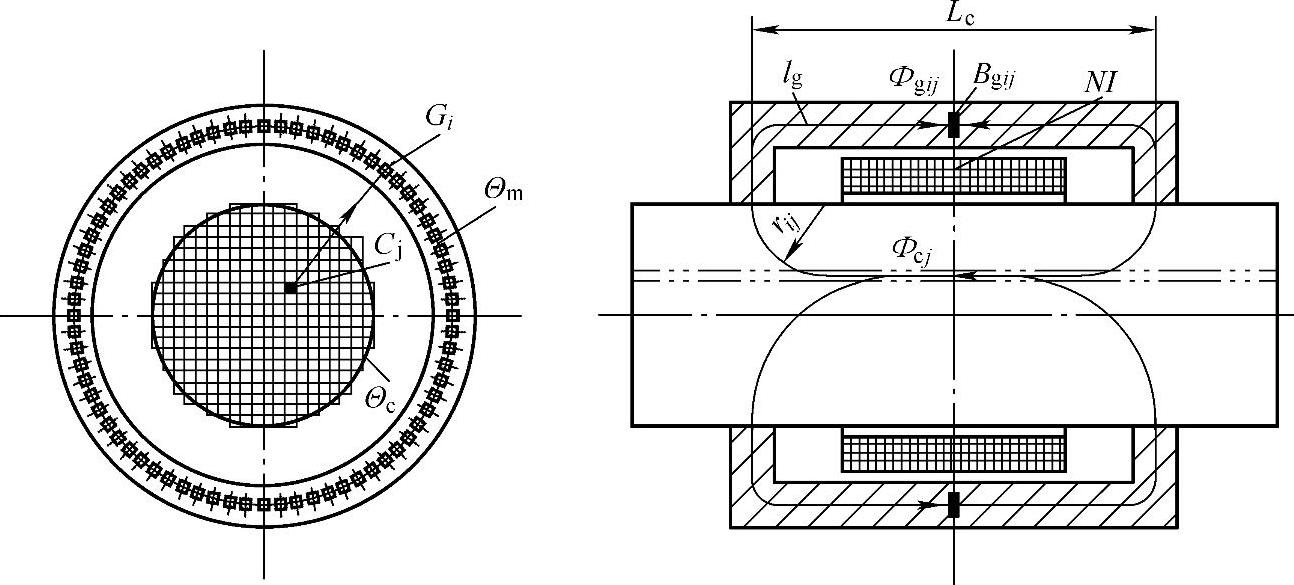
图6-39 拉索截面内的磁通量离散阵列模型

由前述拉索金属截面内磁通量离散阵列模型分析可知，通过拉索截面的磁通量可以看作截面内n个小区域内磁通量的累积和，而每个小区域内磁通量都会通过导磁磁路形成回路，因此通过每个测试点G_i处的磁通量可以认为是拉索截面内n个小区域磁通量通过该测试点的磁通量分量的累积总和。当拉索截面内某个小区域内磁通量发生改变时，通过每个测试点G_i处的磁通量也相应会发生变化。

下面首先考虑拉索截面内某一小区域C_j内物质被磁化后形成的磁通量经过导磁磁路形成闭合回路时，如何在各测试点G_i处进行分配；其次，依次计算拉索截面内所有小区域C_j的磁通量在各测试点G_i处的分布；最后，将所有小区域C_j通过各测试点G_i处的磁通量分量进行累加即可得到该测试点处的磁通量，从而可获取该处的磁感应强度B（G_i）。

如图6-39所示，采用匝数为N，通过电流为I的直流线圈对小段拉索进行磁化，通过截面中某一小区域C_j和任一测试点G_i处可以形成一条磁环路，磁环路包围的电流代数和为NI。根据磁场的环路定理，有

H_gijl_g+H_cj[L_c+（π-2）r_ij]=NI （6-26）

式中，H_gij为拉索截面内小区域C_j的磁通量经过测试点G_i处使G_i处产生的磁场强度；l_g为导磁磁路的等效长度；H_cj为小区域C_j处的磁场强度；L_c为拉索被磁化段的等效长度；r_ij为小区域C_j的磁通量通向测试点G_i方向圆弧路径的半径，称为距离因子。

根据磁通量连续原理，截面内任意小区域C_j的磁通量必须经过导磁磁路形成闭合回路，即有

式中，Φ_gij为拉索截面内小区域C_j的磁通量通过测试点G_i处的磁通量分量；Φ_cj为通过小区域C_j的磁通量。

截面内任意小区域C_j和测试点G_i处磁感应强度B与磁场强度H之间的关系应满足

式中，H_cj、H_gij分别为截面内小区域C_j和测试点G_i处的磁场强度；B_cj、B_gij分别为小区域C_j和测试点G_i处的磁感应强度；μ_cj、μ_g分别为小区域C_j和测试点G_i处的材料相对磁导率。

截面内任意小区域C_j内和测试点G_i处的磁场强度H_cj、H_gij可以认为是均匀分布的，因此磁感应强度与磁通量之间的关系应满足

Φ_cj=B_cjS_cj （6-30）

Φ_gij=B_gijS_gi （6-31）

式中，S_cj、S_gi分别为截面内小区域C_j和测试点G_i处区域的面积。

由式（6-28）和式（6-30）可得

由式（6-29）和式（6-31）可得

将式（6-32）和式（6-33）代入式（6-26）可得

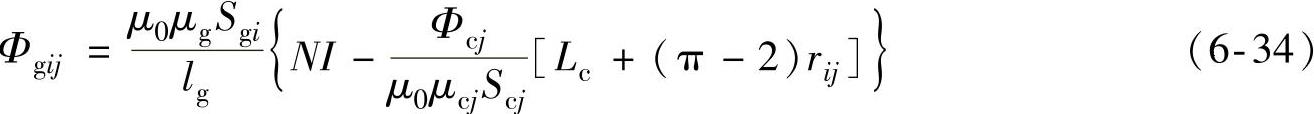
将式（6-34）两边同时求和，可得

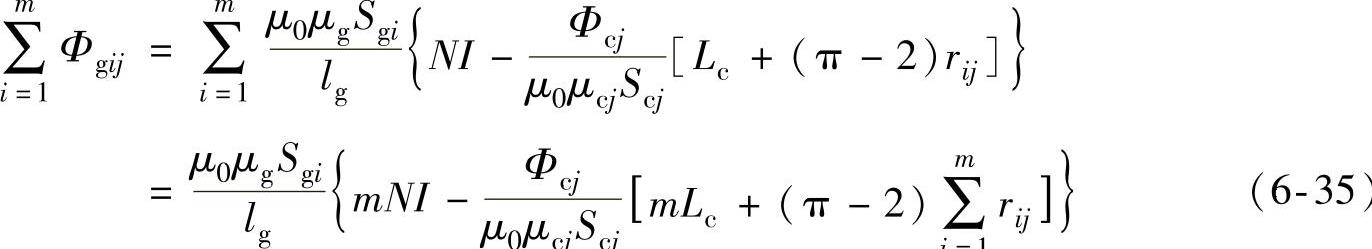
综合式（6-27）和式（6-35）可得

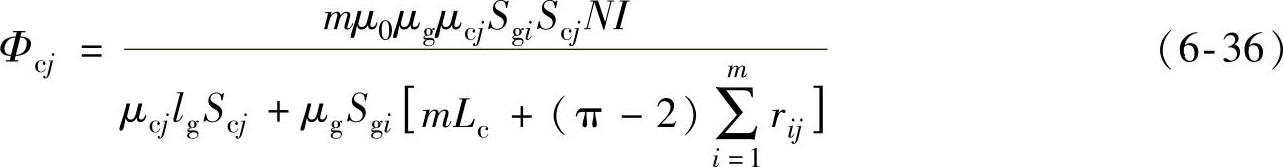(www.xing528.com)

将式（6-31）和式（6-36）代入式（6-34）可得

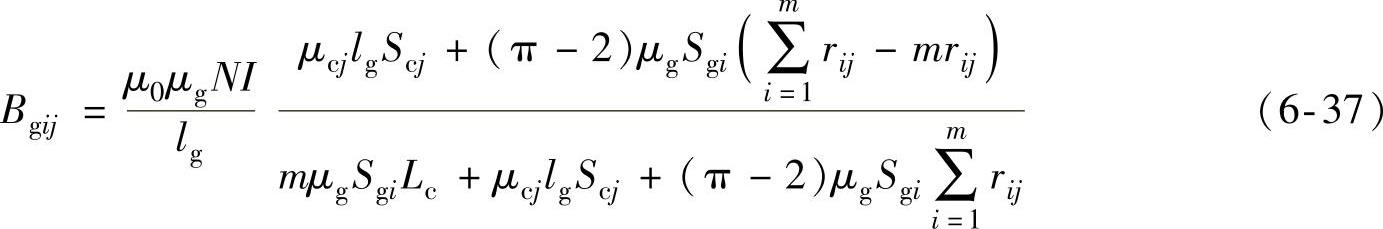
记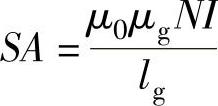，SB=l_gS_cj，SC=mμ_gS_giL_c，SD=（π-2）μ_gS_gi，则式（6-37）变换为

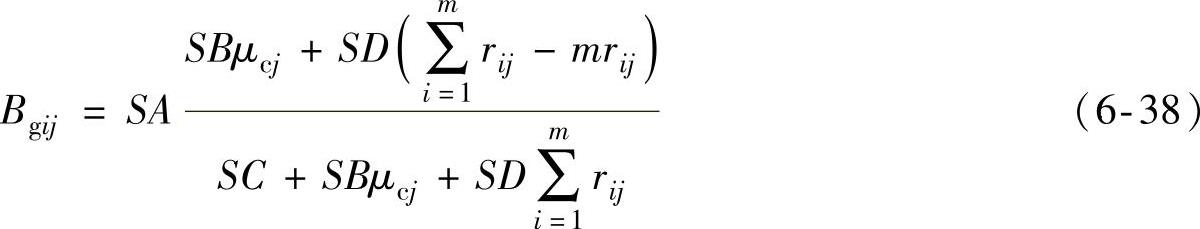
将所有小区域C_j通过测试点G_i处的磁通量分量进行累加即可得到该测试点处的磁感应强度为

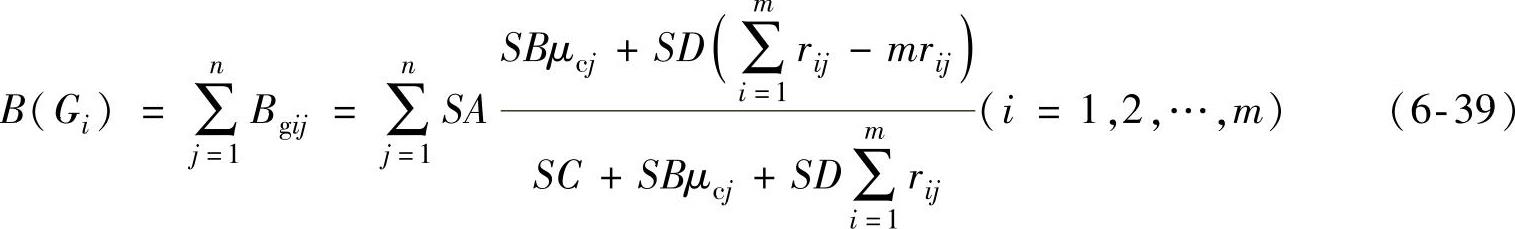
在按式（6-39）计算各测试点G_i（i=1，2，…，m）处的磁感应强度B（G_i）（i=1，2，…，m）时，将所有小区域C_j（j=1，2，…，n）按其内材料是拉索钢丝或空气，分别设置其对应的相对磁导率μ_cj（j=1，2，…，n）为拉索钢丝的相对磁导率或空气的相对磁导率。当某处C_j出现金属截面积变化时，即意味着该处的材料由拉索钢丝变为空气，而C_j与各测试点G_i的距离因子r_ij是有差别的，从式（6-39）可以看出，各测试点G_i（i=1，2，…，m）处的磁感应强度B（G_i）（i=1，2，…，m）是有差别的，即通过式（6-39）将出现截面积金属变化的部位与各测试点获取的测量值之间建立了联系。这就是基于磁通量离散阵列模型的金属截面积变化部位测定计算的正演方程。

采用如图6-40所示的实验装置，实验对象为37根直径为7mm的拉索钢丝捆扎在一起组成的钢丝束；采用1个内径为55mm、长度为80mm、匝数为1000、用线径为1mm的电磁漆包线绕制的磁化线圈用于磁化钢丝束；一个最大能持续恒定提供10A电流的恒流直流电源为磁化线圈提供直流磁化电流，在线圈内形成较均匀的磁场；两个灯罩形低碳钢材料的导磁体对称套在钢丝束上，同时罩住套在钢丝束上的磁化线圈，导磁体外径为146mm、壁厚为8mm，用一个厚度为5mm的铝合金圆环将两个导磁体套接成一体，组合一起的长度为110mm；在铝合金圆环的圆周上均匀设置24个矩形槽，高斯计的探头放置在矩形槽中测试该处的磁感应强度B_g（i）；采用美国LakeShore公司的421型霍尔高斯计，高斯计的测量范围是0.01～20000Gs，精确度为±0.2%。每次实验中，为了减少测试误差，取10组磁感应强度B_g（i）测试值的平均值作为实验结果。

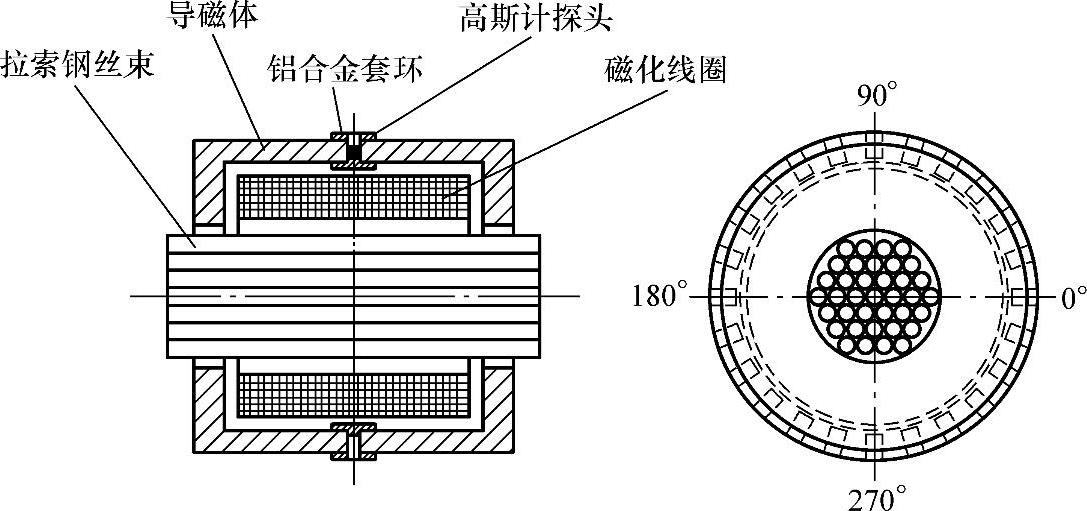
图6-40 金属截面积变化部位测定正演模型实验装置示意图

正演计算模型如图6-41所示，模型中被测区域Θ_c是直径为50mm且刚好包围钢丝束的圆截面，被测区域中离散网格的大小为1mm×1mm，网格的总数量为1976个，测量圆Θ_m的直径为100mm，测量圆Θ_m圆周上均匀布置24个测试点G_i。

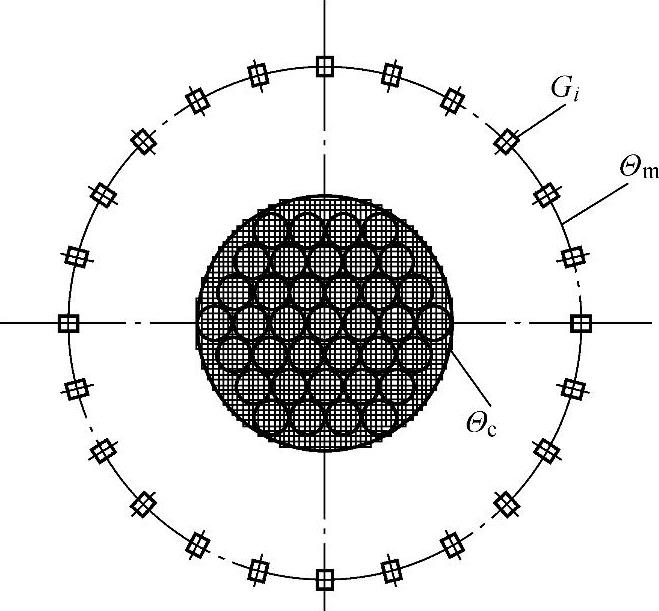
图6-41 拉索钢丝束金属截面积变化部位计算正演模型

下面对图6-42a、图6-43a、图6-44a、图6-45a、图6-46a、图6-47a所示的分别存在单根或多根钢丝损失（各图中虚线圆圈表示钢丝损失的位置）的拉索钢丝束采用上述金属截面积变化部位测定方法的正演模型进行计算，并通过实验进行验证。

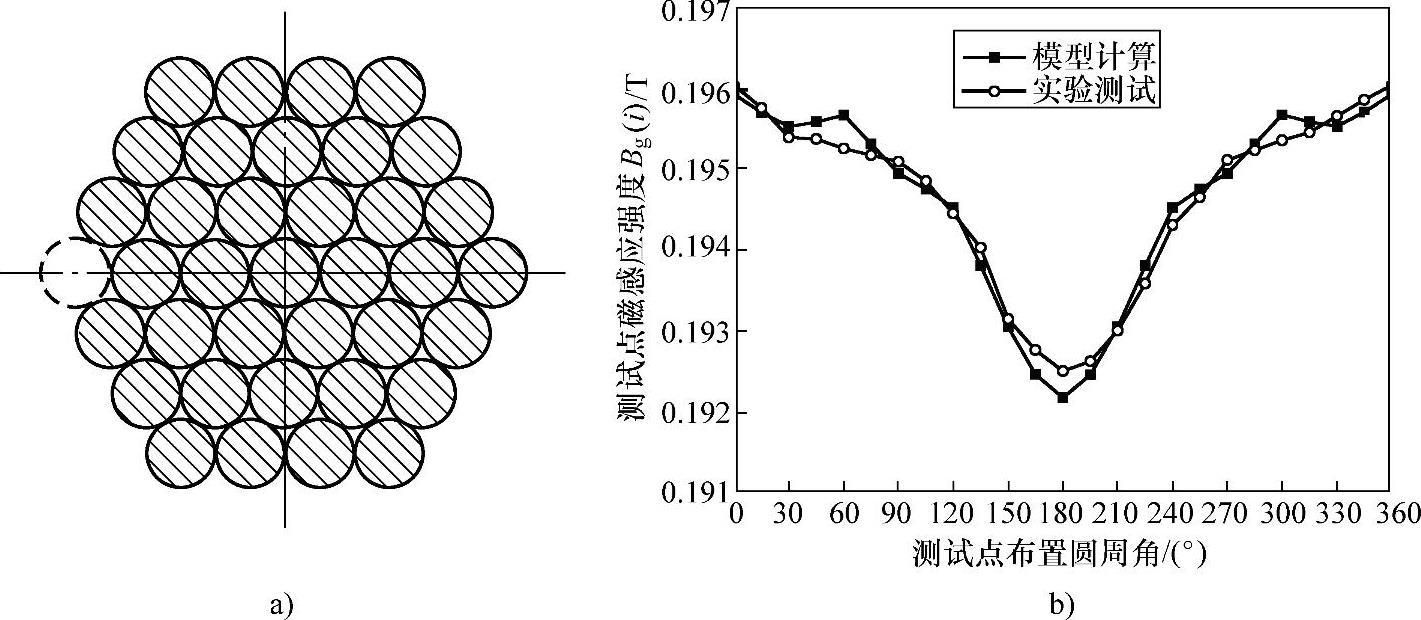
图6-42 拉索钢丝束外部单根钢丝损失

a）钢丝束截面示意图 b）模型计算及实验测试对比

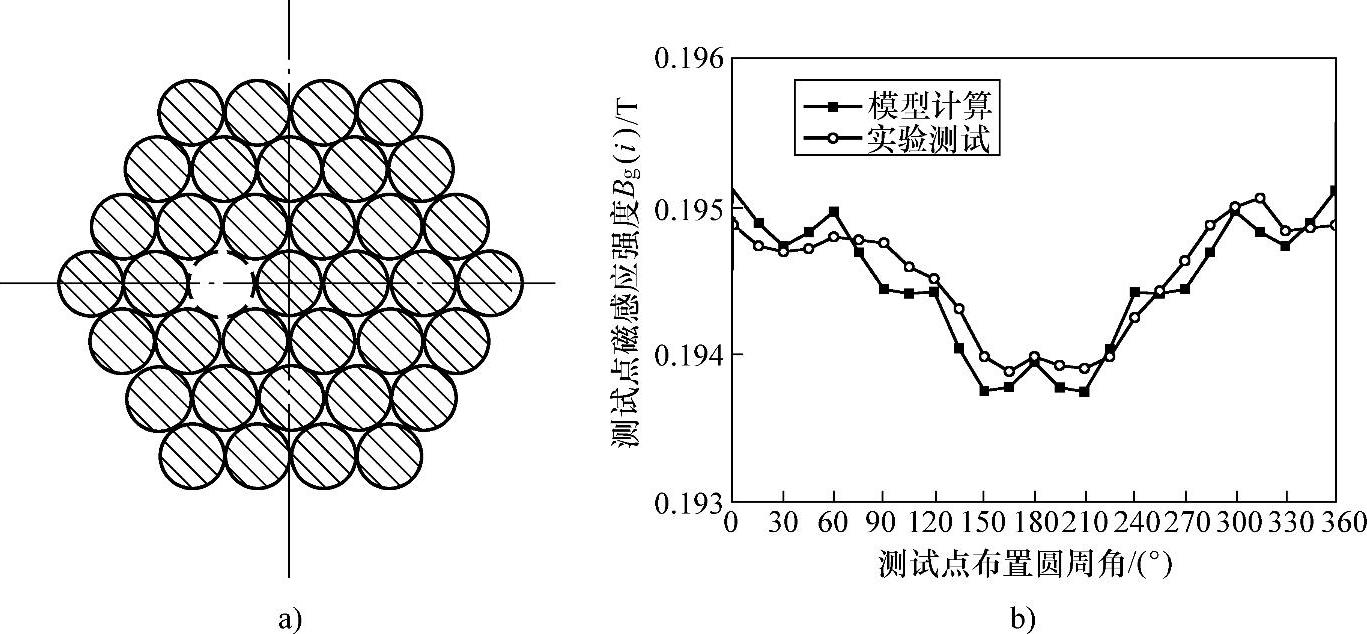
图6-43 拉索钢丝束内部单根钢丝损失

a）钢丝束截面示意图 b）模型计算及实验测试对比

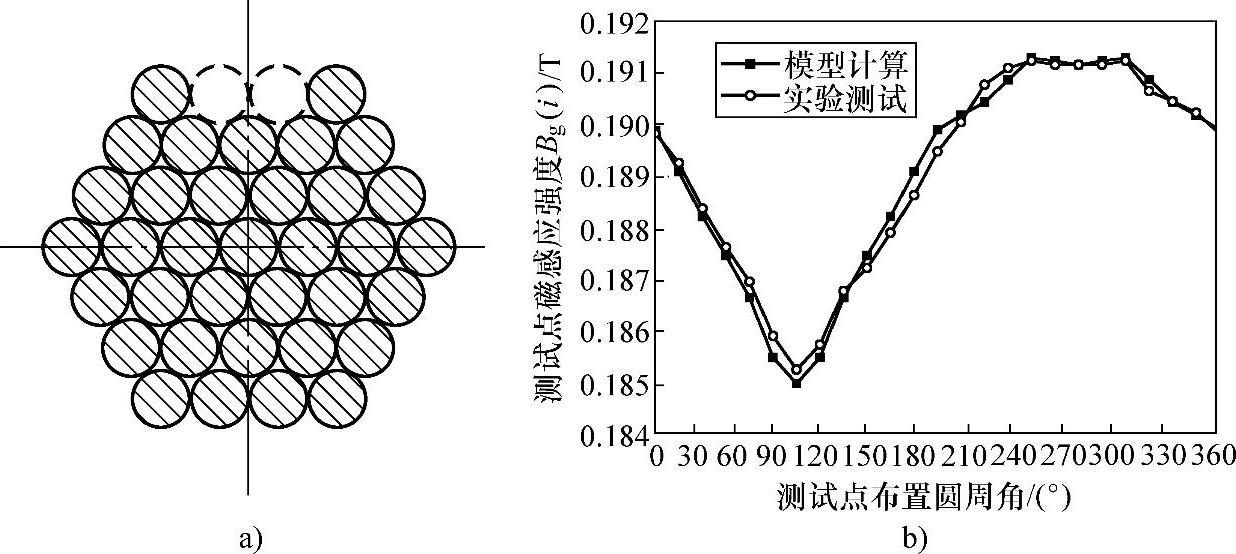
图6-44 拉索钢丝束外部两根钢丝损失

a）钢丝束截面示意图 b）模型计算及实验测试对比

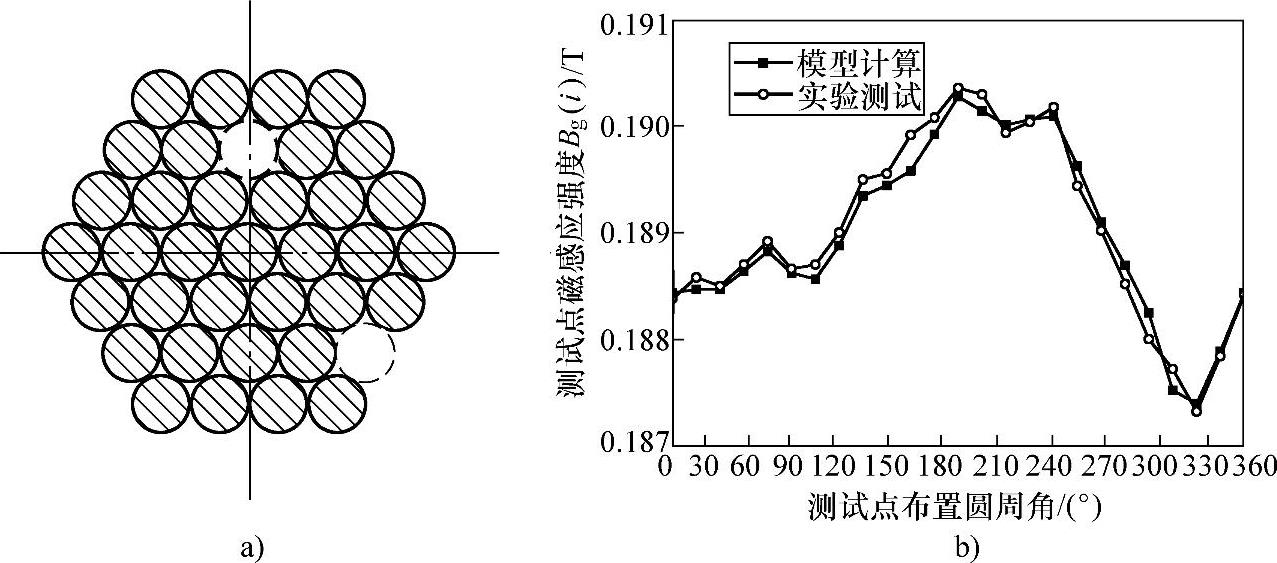
图6-45 拉索钢丝束内外部两根钢丝同时损失

a）钢丝束截面示意图 b）模型计算及实验测试对比

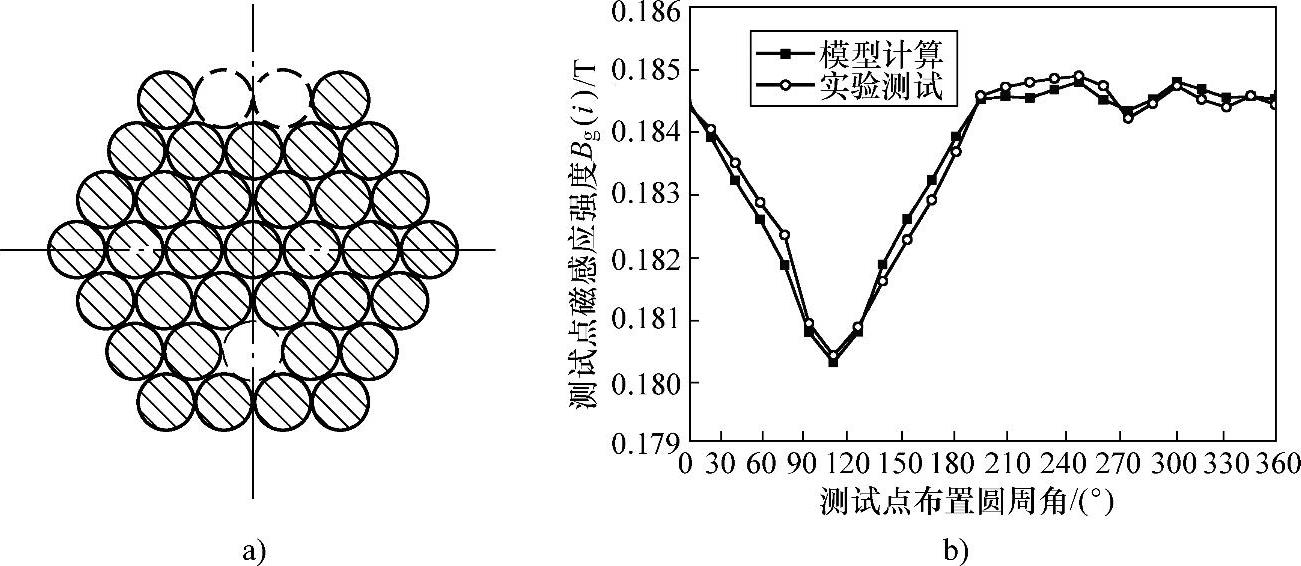
图6-46 拉索钢丝束内外部多根钢丝同时损失

a）钢丝束截面示意图 b）模型计算及实验测试对比

模型计算结果和实验测试结果分别如图6-42b、图6-43b、图6-44b、图6-45b、图6-46b、图6-47b所示，对比模型计算和实验测试的结果可以看出，模型计算结果与实验测试结果基本吻合，证明了金属截面积变化部位测定方法正演模型的正确性。模型计算结果与实验测试结果均明显反映出：越靠近金属损失的测试点，其获取的幅值越小，远离金属损失的测试点，其获取的幅值越大；金属损失处越靠钢丝束外部则所有测试点获取的最大幅值与最小幅值之差越大，相反越小。通过上述两条规律，在实际应用时可以大致判断出金属损失所在的相位和在钢丝束内所处的层次，可以对拉索金属截面积变化进行粗定位。