基于导出磁通量的拉索金属截面积变化量测量方法优化

图6-26所示为基于导出磁通量的拉索金属截面积变化量测量原理图。磁化线圈通电后，线圈内部的拉索钢丝束被磁化，钢丝束截面内的轴向磁通量Φ_c与其截面积S_c有关，即

Φ_c=B_cS_c （6-4）

式中，B_c为拉索钢丝束被磁化后其内部产生的磁感应强度。

从式（6-4）可以看出，拉索钢丝束截面内轴向磁通量的大小与截面积大小有关，因此若能测量出拉索钢丝束截面内轴向磁通量，就能间接地得出拉索钢丝束金属截面积。

基于导出磁通量的拉索金属截面积变化量测量方法的基本原理是，首先将拉索钢丝束截面内的轴向磁通量Φ_c引导出来，图6-26所示的导磁衔铁由高磁导率的低碳钢制成，能极大程度地将拉索钢丝束内部的磁通量导入其内，磁通量将在拉索钢丝束、导磁衔铁及两者之间的空气隙形成磁回路，当拉索钢丝束内部的磁通量发生变化时，根据磁通量连续原理，导磁回路中其他部位通过的磁通量发生相应变化，因此可以在导磁回路的任意部位设置磁敏元件来探测磁通量的变化，即可获取金属截面积变化的信息。

从上述基于导出磁通量的拉索金属截面积变化量测量基本原理可知，通过设置导磁衔铁将拉索钢丝束截面内的轴向磁通量引导至导磁磁路中，再通过在导磁磁路中设置磁敏感元件来测量该磁通量，而拉索钢丝束截面内的轴向磁通量中包含与钢丝束截面积相关的信息，因此可以间接实现拉索钢丝束截面积测量。但是要采用该方法实现准确、便捷地测量拉索钢丝束截面积，首先必须清楚磁敏感元件的测量值与拉索钢丝束截面积间呈现的关系。以下将通过建立该测量方法的等效磁路模型来分析磁敏元件的测量值与拉索钢丝束截面积之间的关系。

图6-26所示的基于导出磁通量的拉索金属截面积变化量测量的等效磁路模型如图6-27所示。

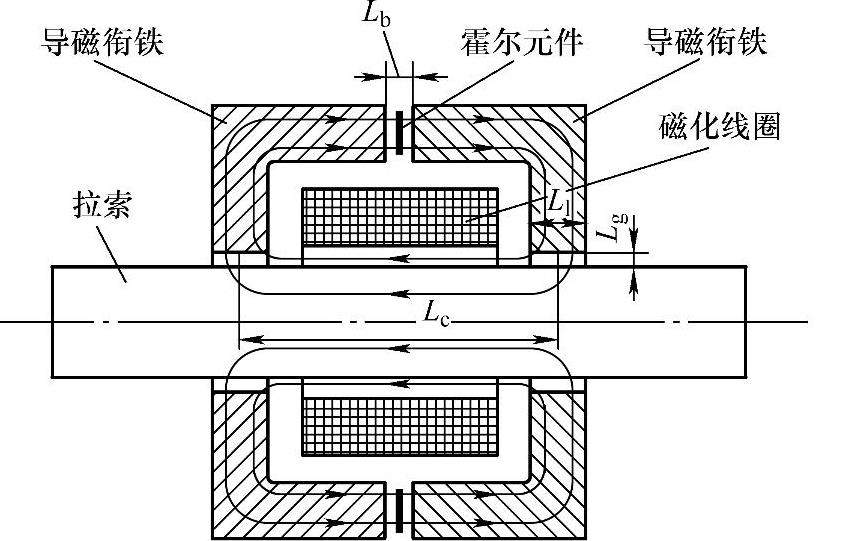
图6-26 基于导出磁通量的拉索金属截面积变化量测量原理

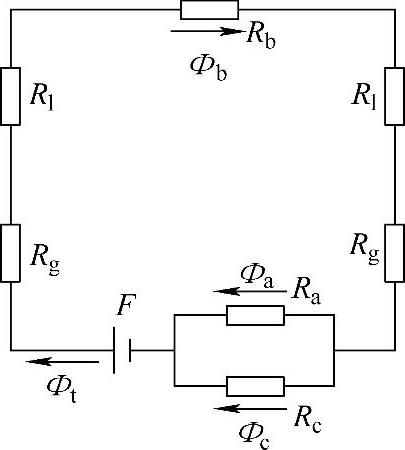
图6-27 基于导出磁通量的拉索金属截面积变化量测量磁路模型

图中各参数的含义如下：

F——磁化线圈提供的磁动势；

R_a——磁化线圈内空气的磁阻；

R_c——被磁化拉索段的磁阻；

R_g——衔铁组与拉索间空气隙的磁阻；

R_l——衔铁组的磁阻；

R_b——磁敏元件测量间隙处的磁阻；

Φ_a——磁化线圈内空气的磁通量；

Φ_c——拉索中截面内的磁通量；

Φ_t——磁化线圈内磁通量总和；

Φ_b——磁敏元件测量间隙处的磁通量。

分析图6-27所示的磁路模型，可得到如下四个等式：

（2R_g+2R_l）Φ_t+R_bΦ_b+R_cΦ_c=F （6-5）

Φ_b=Φ_t （6-6）

Φ_t=Φ_a+Φ_c （6-7）

R_aΦ_a=R_cΦ_c （6-8）

将式（6-6）～式（6-8）代入式（6-5）并化简可得

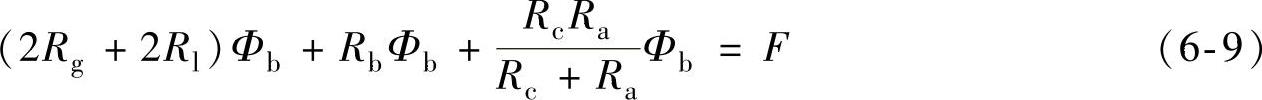
磁化线圈内空气的磁阻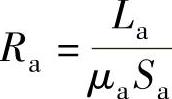，式中L_a、μ_a、S_a分别为磁化线圈内空气磁化段的长度、空气的磁导率和磁化线圈内空气的截面积。被磁化拉索段的磁阻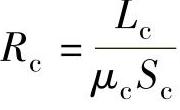，式中L_c、μ_c、S_c分别为拉索被磁化段的长度、拉索的磁导率和拉索的截面积。由于L_a和L_c大小相当，S_a和S_c大小相当，而μ_a＜＜μ_c，所以R_a＞＞R_c，得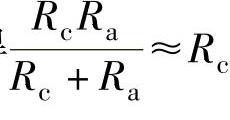，式（6-9）可简化为（2R_g+2R_l+R_b+R_c）Φ_b=F。

令R_s=2R_g+2R_l+R_b，有。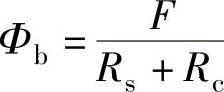

对于两段相同材料（材料的磁导率为μ_c）、相同长度（其平均磁化长度为L_c）而截面积分别为S_c1、S_c2的拉索C₁、C₂有

式（6-10）、式（6-11）中，Φ_b1、Φ_b2分别为检测拉索C₁、C₂时，磁敏元件测量间隙处的磁通量；R_c1、R_c2分别为拉索C₁、C₂的磁阻。

式（6-11）除以式（6-10）得

变换，得

因为R_s＞＞R_c2，有R_s≈R_s+R_c2，所以

将Φ_b1=B_b1S_b，Φ_b2=B_b2S_b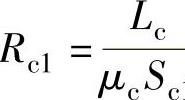，1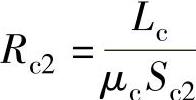，代入式（6-14）得

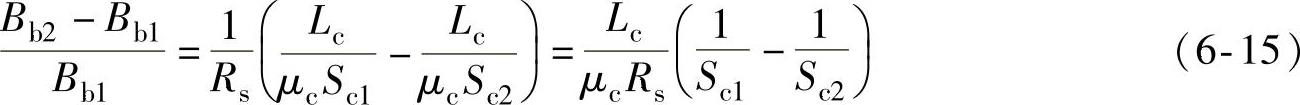
式中，B_b1、B_b2分别为检测拉索C₁、C₂时，磁敏元件测量间隙处的磁感应强度；S_b为磁敏元件测量间隙处的磁路的截面积，对于确定的仪器，S_b值始终保持不变。对拉索金属截面积变化量进行测量时，不妨设拉索金属截面积变化率为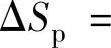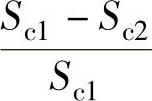，则

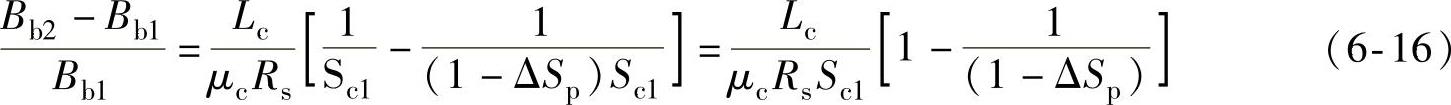
对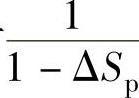按ΔS_p在ΔS_p=0处进行二阶泰勒展开，即

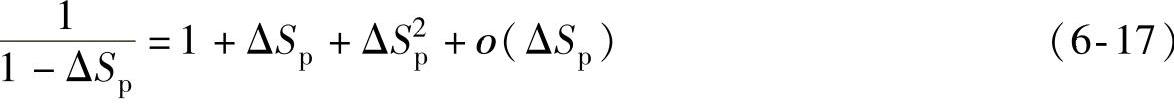
式中ο（ΔS_p）为ΔS_p的高阶量，对于较小的ΔS_p值，ο（ΔS_p）为一极小值，可忽略。因此，有

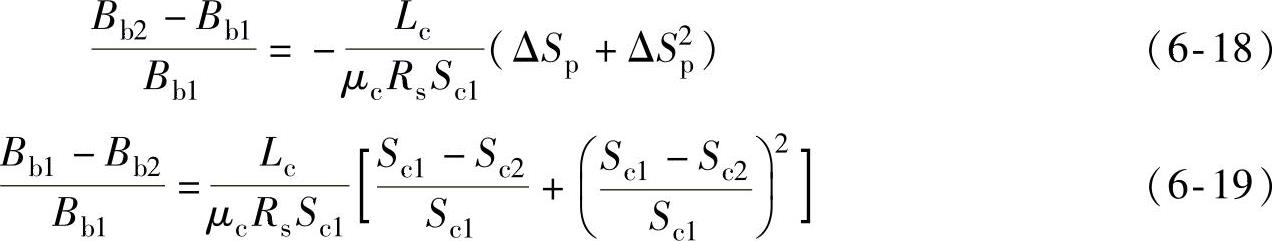
记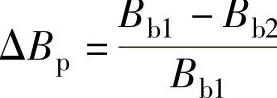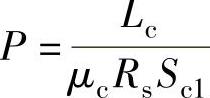，，则

ΔB_p=P（ΔS_p+ΔS²_p） （6-20）

式（6-20）中，P称为测量系数。

如选霍尔元件作为磁敏元件时，霍尔元件在其正常工作量程内输出电压值U与测量处磁感应强度B成正比，即

U=K_HB （6-21）

式中，K_H为霍尔元件的灵敏度系数。

相应地有

ΔU_p=ΔB_p=P（ΔS_p+ΔS²_p） （6-22）

式中，ΔU_p为霍尔元件输出电压变化率。

式（6-20）表示的是磁敏元件测量处磁感应强度变化率与拉索截面积变化率之间的关系。当拉索金属截面积变化率较小时，即ΔS_p较小时，磁敏元件测量处磁感应强度变化率ΔB_p与拉索金属截面积变化率ΔS_p成正比；当拉索金属截面积变化率继续增大时，磁感应强度变化率ΔB_p与ΔS_p+ΔS²_p或更高阶的ΔS_p成正比。对于在役拉索而言，其金属截面积变化率通常较小，因此拉索金属截面积变化率ΔS_p与磁敏元件测量处磁感应强度变化率ΔB_p大致成正比，通过在测量断口处设置磁敏元件即可检测拉索金属截面积变化率。如磁敏元件为霍尔元件，则霍尔元件输出电压变化率ΔU_p与拉索金属截面积变化率ΔS_p成线性关系，如式（6-22）所表达的关系。(www.xing528.com)

在一定的误差范围内可以利用ΔU_p=PΔS_p所表达的关系应用该测量方法对拉索金属截面积变化量进行线性测量，但在具体实施测量前必须确定测量系数P值。从式（6-19）和式（6-20）可知，需已知L_c、μ_c、R_s、S_c1的数值才能确定测量系数P值，而L_c、μ_c、R_s的具体数值较难准确得到，但对于确定的拉索金属截面积变化量测量传感器和拉索而言，L_c、μc、Rs是定值，因此可以通过采用若干段截面积已知、材料特性与被测拉索相同、长度大于衔铁长度的标样钢丝来标定测量系数P值。

确定测量系数P值后，可认为在对该拉索后续进行的金属截面积变化率测量过程中，该测量系数P值保持不变，根据下述步骤即可得到拉索长度方向各处金属截面积相对于参考区域金属截面积的变化率。

首先获取参考区域金属截面积S₀和测量该截面积时霍尔元件的输出电压幅值U₀；当检测某一截面积为S_i的待检测区域时，霍尔元件的输出电压幅值为U_i。

根据式（6-22）可得到每一待检测区域的截面积S_i相对于初始区域截面积S₀的金属截面积变化率

并可得到该检测区域的截面积S_i

S_i=（1-ΔS_pi）S₀ （6-24）

由上述分析可知，当拉索金属截面积变化率较小时，霍尔元件输出电压变化率ΔU_p与拉索金属截面积变化率ΔS_p成正比，即

ΔU_p≈PΔS_p （6-25）

若式（6-25）成立，则可以通过霍尔元件输出电压变化率ΔU_p的值来获取拉索金属截面积变化率ΔS_p的值。而实际上，由于磁场的非线性特征，图6-27中的磁路参数（如R_g、R_l、R_b、μ_c、L_c等）将随着测量状况发生变化，这些因素对该测量方法的影响程度是否足以破坏以上所述ΔU_p与ΔS_p之间的线性关系，或者这些因素对测量方法会不会造成太大的影响，还需通过实验来验证。式（6-25）中的ΔU_p与ΔS_p之间的线性关系成立是基于ΔS_p值较小时，但ΔS_p具体在多大范围内能保证ΔU_p与ΔS_p之间可以采用线性关系表述而不产生较大的误差，这些均需通过实验结果来分析。

图6-28所示是实验装置示意图。一个内径为80mm、长度为145mm、匝数为2800、用线径为1mm的电磁漆包线绕制的磁化线圈用于磁化钢丝束；四个由磁导率较高的低碳钢制作的导磁衔铁组，两个对称布置的L形导磁衔铁构成一个导磁衔铁组，两个导磁衔铁间预留缝隙可以布置一个霍尔元件，导磁衔铁间预留缝隙的宽度可调，实验中缝隙宽度固定为7mm，每个L形导磁衔铁的横截面尺寸为40mm×40mm，L形两边长均为120mm；一个最大能持续恒定提供10A电流的恒流直流电源为磁化线圈提供直流磁化电流，在线圈内形成较均匀的磁场；用196根直径为2.76mm、长度为1m的粗钢丝及10根直径为1.56mm、长度为1m的细钢丝组成的钢丝束模拟拉索钢丝束；钢丝束放置在一个外径为75mm、壁厚为2mm、长为800mm的硬质塑料圆管内，以保证钢丝束聚集在一起，同时方便从钢丝束中抽取钢丝。磁化线圈套在塑料管外，基本保证和塑料管同心，导磁衔铁组横跨磁化线圈，导磁衔铁组两端部贴近圆管表面，两者间空气间隙为10mm，四个导磁衔铁组沿圆管周向均匀布置；霍尔元件输出经过滤波及电压偏置调节电路、放大器后，再经信号采集卡输入计算机，计算机上显示经滤波、偏置及放大后的霍尔元件输出电压幅值。

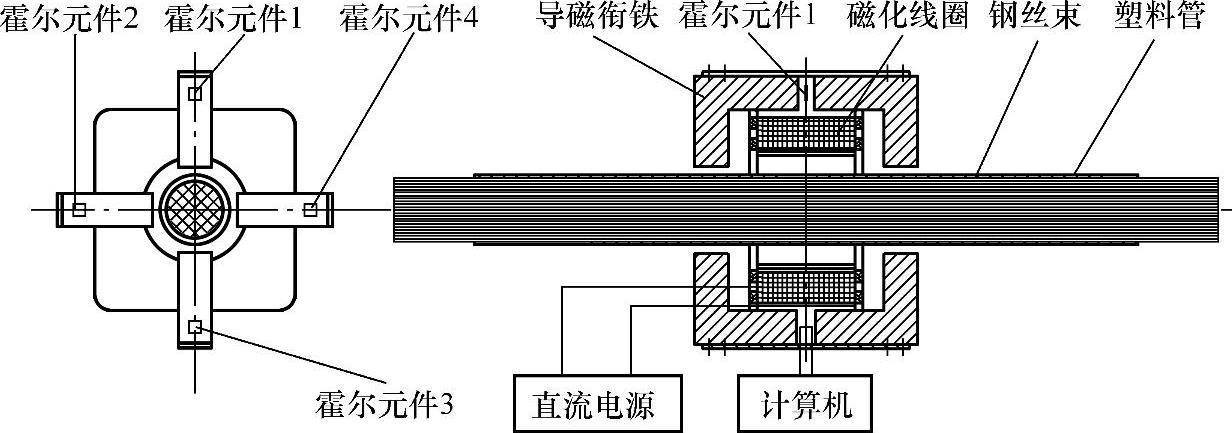
图6-28 基于导出磁通量的拉索金属截面积变化量测量实验装置示意图

实验中，通过从206根钢丝束中抽取不同根数的钢丝来模拟钢丝束截面积的变化，钢丝束的总截面积为1191.75mm²，1根直径为1.56mm细钢丝的截面积为1.91mm²，1根直径为2.76mm的粗钢丝的截面积为5.98mm²。当从206根钢丝束中抽出1根直径为1.56mm的细钢丝时，相当于钢丝束截面积减小0.16%；当从206根钢丝束中抽出1根直径为2.76mm的粗钢丝时，相当于钢丝束截面积减小0.50%。以下每次实验过程中均采用抽出钢丝后不重新放回的方法，模拟钢丝束截面积变化率从0～20.69%的变化。其中，在0～1.6%范围内，每次按0.16%变化；在1.6%～20.69%范围内，每次按0.50%变化。

实验中设置磁化线圈的磁化电流为3A，进行截面积变化测量，每次均记录四个霍尔元件的输出电压幅值之和，测量结果如图6-29所示。图中以ΔS_p为横坐标，以ΔU_p为纵坐标，直线为ΔS_p与ΔU_p之间关系的拟合直线。从图6-29中可以看出，各数据点间基本成线性关系，对数据点进行线性拟合，可得到ΔU_p与ΔS_p之间的关系式为ΔU_p=0.8058ΔS_p。

对图6-30a所示的在不同径向位置的截面积变化率均为0.5%的截面积变化进行测量，实验时在钢丝束试样中分别设置截面积变化位于截面的不同径向位置，从截面中心开始沿径向依次改变截面积变化的部位，每次改变的径向距离为3mm，每次截面积变化率均为0.5%，共测量14个径向位置，测量结果如图6-30b所示。从图中可以看出，在不同的径向位置，截面积变化率测量结果基本都在真值0.5%附近波动，而不受径向位置改变的影响，测量值的波动是正常的测量随机误差。

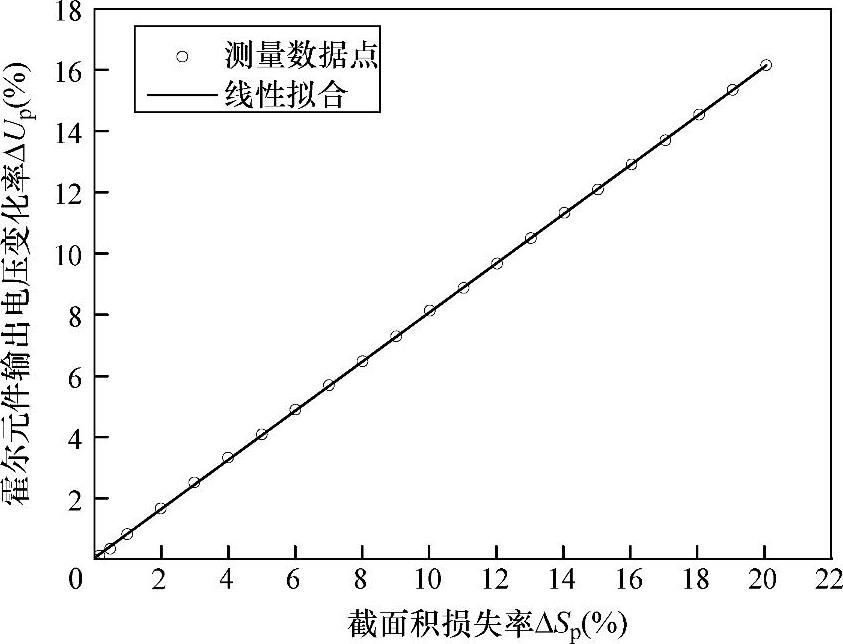
图6-29 基于导出磁通量的拉索金属截面积变化量测量实验结果

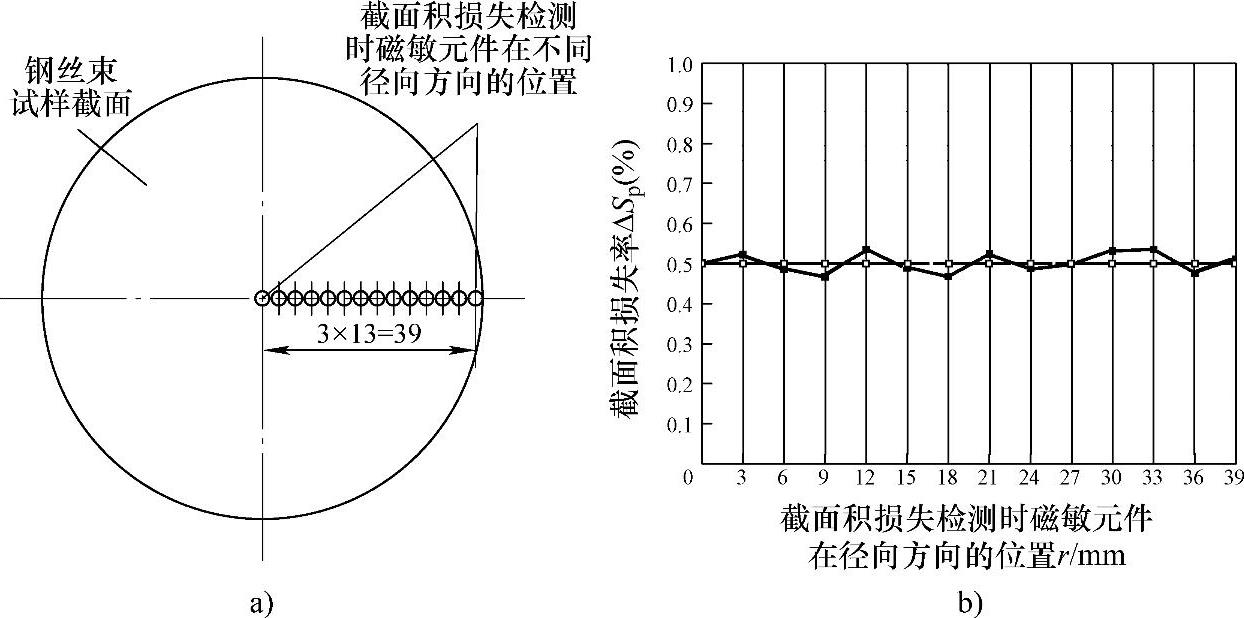
图6-30 不同径向位置截面积变化测量结果

a）不同位置测量示意图 b）不同位置测量结果比较图

1.导磁磁路数量对测量的影响

采用2个相隔180°布置的导磁磁路，分别设置磁化线圈的磁化电流为0.5A、1A、2A、3A、4A、4.5A、5A，进行7次截面积变化测量。

图6-31所示为不同磁化电流下，霍尔元件输出电压变化率ΔU_p与拉索金属截面积变化率ΔS_p之间的关系曲线图。从图6-31中可以看出，采用2个相隔180°布置的导磁磁路进行截面积测量，当磁化电流为3A、4A、4.5A、5A时，ΔU_p与ΔS_p之间呈现较好的线性关系。

采用1个导磁磁路，分别设置磁化线圈的磁化电流为0.5A、1A、2A、3A、4A、4.5A、5A，进行7次截面积变化测量。

图6-32所示为不同磁化电流下，霍尔元件输出电压变化率ΔU_p与拉索金属截面积变化率ΔS_p之间的关系曲线图。从图6-32中可以看出，采用1个导磁磁路进行截面积测量，各磁化电流下ΔU_p与ΔS_p之间的线性度均较差。

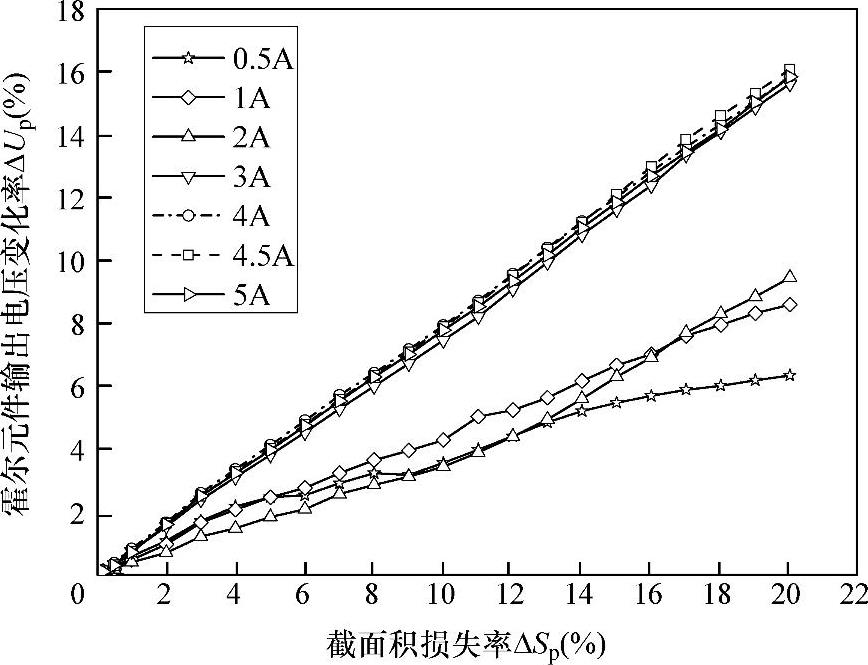
图6-31 2个导磁磁路截面积变化率测量实验结果

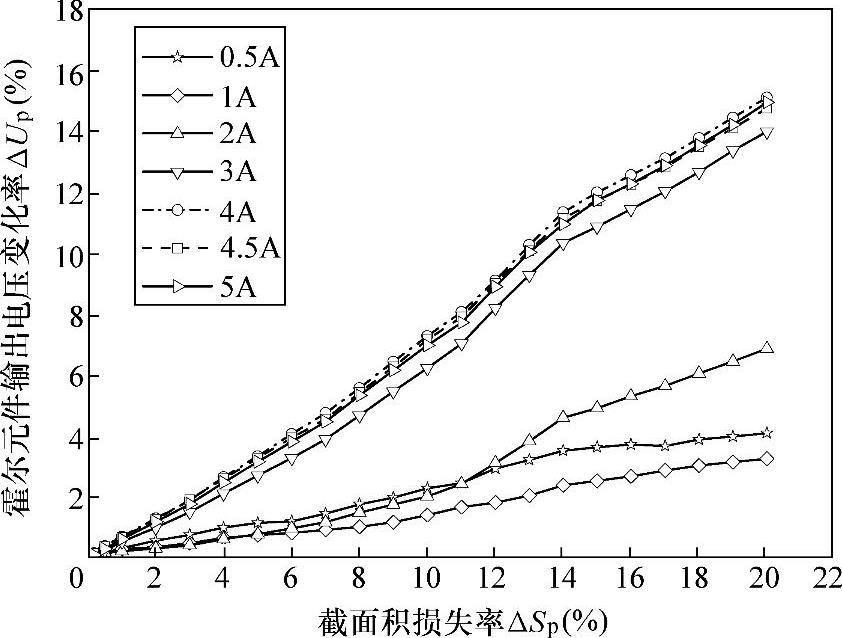
图6-32 1个导磁磁路截面积变化率测量实验结果

2.霍尔元件放置位置对测量的影响

由基于导出磁通量的拉索金属截面积变化量测量原理可知，拉索被磁化时，拉索和衔铁及两者间的空气间隙共同形成磁回路，拉索内产生的磁通量首先被收集至衔铁一端，再集中通过衔铁到达另一端，最后再散开回到拉索中，形成一个闭合回路。磁通在拉索和衔铁端部间通过时呈分散不均匀的伞状分布，而通过衔铁中间部位时呈相对均匀的分布。

与霍尔元件放置在衔铁中间部位相比，将霍尔元件放置在衔铁端部的测量精度应较低，原因是通过衔铁端部的磁通量的分布区域较广且不均匀，霍尔元件放置在衔铁端部时，很难收集磁通量的整个信息。当截面积变化位置距离霍尔元件较近时，霍尔元件测量值变化最大；当截面积变化位置距离霍尔元件较远时，霍尔元件测量值变化最小，即截面积变化位置将对测量结果产生较大影响。而通过衔铁中间部位的磁通量相对集中且均匀，因此霍尔元件放置在衔铁中间部位时，其测量值就是衔铁中截面磁感应强度的平均值，当衔铁中的磁通量发生变化时，霍尔元件的测量值变化与磁通量变化成线性关系。

将霍尔元件放置在衔铁端部，分别设置磁化线圈的磁化电流为2A、3A、4A、4.5A、5A，进行5次截面积变化测量。图6-33所示为不同磁化电流下，霍尔元件输出电压变化率ΔU_p与拉索金属截面积变化率ΔS_p之间的关系曲线图。

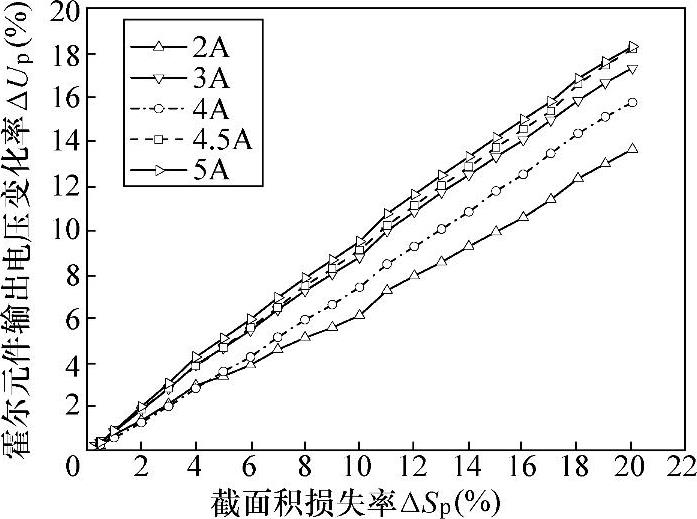
图6-33 霍尔元件放置在衔铁端部时截面积变化率测量实验结果

3.在役拉索应力对测量的影响

在役拉索内部钢丝工作时所受应力约为600MPa，磁化过程中应力对磁化的进程可以起到促进或阻碍的作用。因此，应用磁性测量法对在役拉索实施金属截面积变化率测量时，应考虑拉索所受应力对测量的影响。

通常斜拉桥拉索由多根ϕ5mm或ϕ7mm的钢丝组成，钢丝的材料多为高强度碳素弹簧钢，属高碳钢。为了深入研究拉索钢丝的力磁耦合行为，研制了力磁耦合测试实验装置，包括拉索钢丝加载实验台、拉索钢丝磁化及磁参数测量装置。利用这套实验装置，分别进行了拉索钢丝在不同应力和不同磁场下的力磁耦合实验。

进行实验测试时，先由计算机设定要测量的参数和磁场数值，指示磁化电源控制单元向螺线管输入电流，磁感应强度测量线圈的感应电压经电子磁通积分器及A-D转换器接入计算机，然后计算机对这些数据进行处理和计算，并设定下一步的测量参数和磁场数值。这是一次小的工作循环，许多这样的小循环构成了一个试件的全部测量过程。

此外，为了消除剩磁对磁化曲线的影响，在每次磁化测量前，需对试件进行退磁处理。本实验中采用直流换向退磁，即借助于磁化装置先将试件磁化到饱和，然后用电流换向开关进行换向，同时将退磁电流逐步减小到零。

实验中运用实验系统的加载装置对钢丝施加拉力，使钢丝的拉应力从0MPa开始，每隔100MPa固定钢丝所受拉应力不变，首先对钢丝进行退磁处理，再将其磁化至近饱和，测出磁化曲线，测试完成后，应力值增加100MPa。如此测试，直至钢丝最大应力达到1000MPa。

实验系统组成示意图如图6-34所示，主要由试件、加载装置、磁化装置、磁感应强度测量装置、监控和采集装置组成。图6-35所示为实验系统实物照片。

实验采用斜拉桥拉索常用的ϕ5mm钢丝作为试件，试件长度为800mm。钢丝材料为高强度碳素弹簧钢，其抗拉强度R_m=1570MPa，工作应力为600MPa。

图6-36所示为ϕ5mm钢丝在不同拉应力作用下，经实验测试获得的磁化曲线；图6-37所示为对应的相对磁导率与磁场强度的关系曲线。从图6-36和图6-37中可以看出，拉应力对拉索钢丝的磁化有明显的影响，具体表现为拉应力将阻碍拉索钢丝的磁化，即在相同磁场H作用下，随着拉应力的增大，拉索钢丝的磁感应强度B和相对磁导率μ_r均降低，且拉应力越大，越不易被磁化至饱和。从图6-37还可以看出，在较小磁场强度H的作用下，拉应力对拉索钢丝相对磁导率的影响较大；但在较大磁场强度H的作用下，拉应力对相对磁导率的影响甚小。如图6-38所示，在H=10650A/m时，分别在拉应力为0MPa和1000MPa作用下，钢丝相对磁导率的差值不到20。

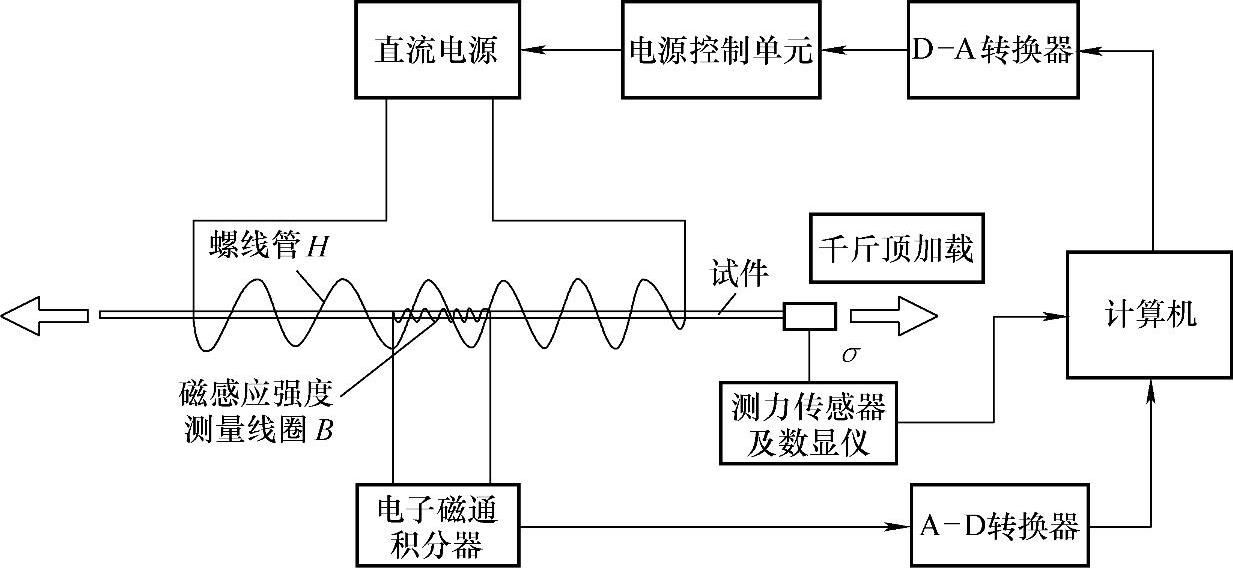
图6-34 实验系统组成示意图

图6-35 实验系统实物照片

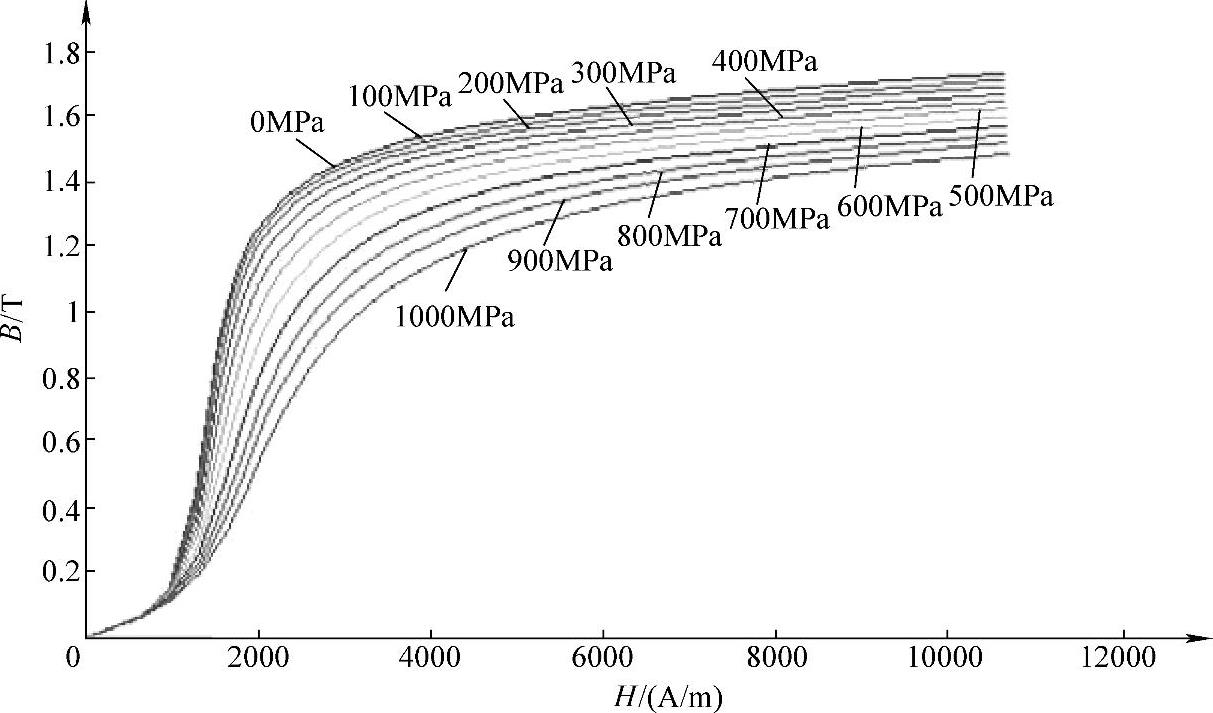
图6-36 ϕ5mm钢丝在不同应力作用下的磁化曲线

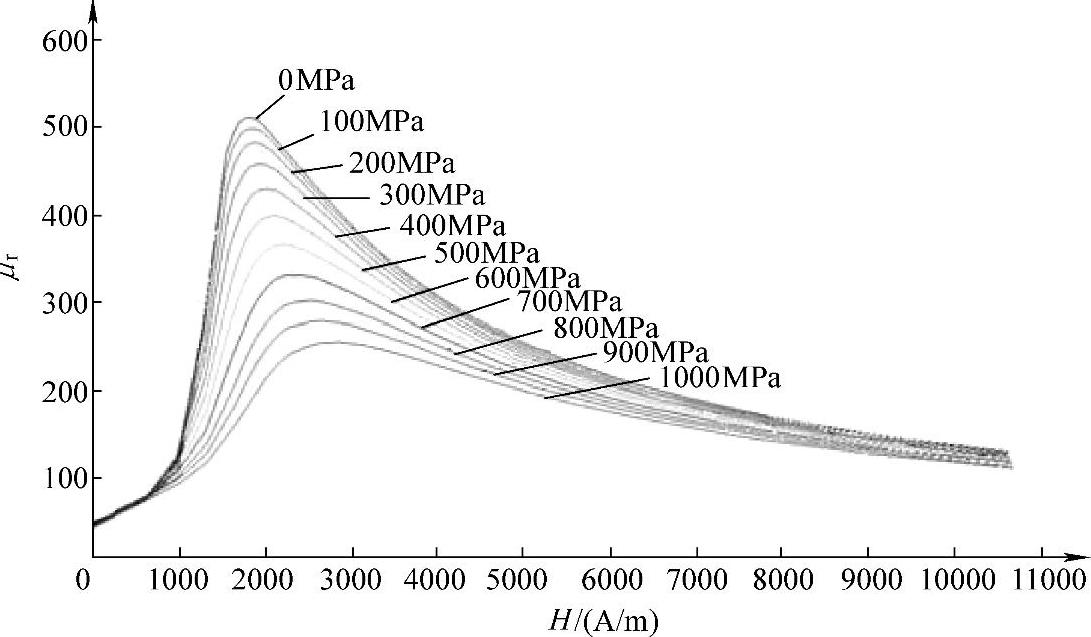
图6-37 ϕ5mm钢丝在不同应力作用下相对磁导率与磁场强度的关系曲线

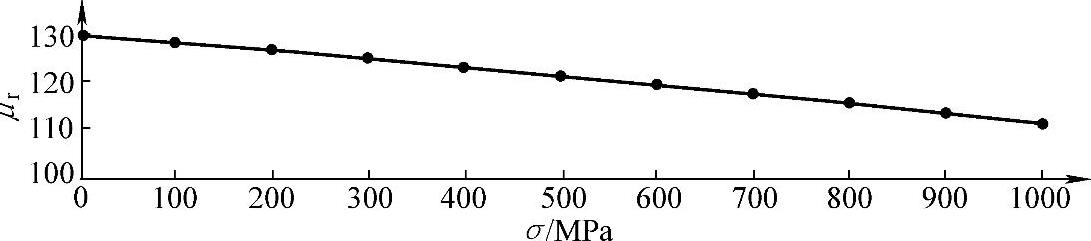
图6-38 磁场强度H=10650A/m时相对磁导率与拉应力的关系曲线

对在役拉索进行磁性测量时，必须要考虑在役拉索承载状态下应力对测量的影响。首先，为减小应力对测量的影响，用于测量仪器标定的样索应模拟在役拉索的承载状态，若选用无应力样索进行标定，则需进行修正补偿；其次，在役拉索金属截面积变化量测量时，拉索钢丝束的磁参数应选取正常工作应力下的磁特性参数；第三，当拉索出现金属截面积变化时，其工作应力产生波动，相应磁特性也产生波动，将对检测产生影响，为减小这种影响，应尽量提高拉索的磁化程度，因为拉索被磁化的程度越高，其磁特性受应力的影响越小。