完整信号下的缺陷分类量化方法优化

以人工神经网络对缺陷进行量化通常采用统一的网络进行缺陷参数预测，并未考虑不同形状缺陷的漏磁检测信号之间的差异，结果导致缺陷的量化误差较大。为了提高缺陷的量化精度，首先基于三维漏磁信号对缺陷进行分类，再针对不同类型的缺陷，分别训练相应的人工神经网络以用于相应类别缺陷的量化。

首先，针对凹坑、水平沟槽、切向沟槽这三种类型的缺陷，建立用于缺陷分类的RBF人工神经网络。由于不同种类缺陷三维漏磁信号之间的差异较大，通过提取特征量值的方法，难以得到合适的缺陷分类人工神经网络的输入信号。为此，提出缺陷漏磁信号水平分量的网格平均处理方法，用于获取RBF分类网络的输入信号。并通过缺陷分类试验，验证所建立的RBF分类网络的分类准确度。

其次，针对凹坑、水平沟槽、切向沟槽三类缺陷，分别构建用于缺陷几何尺寸量化的BP（back propagation）人工神经网络。为了控制所构建BP人工神经网络的复杂度，以节约对所构建BP人工神经网络的训练时间，在网络训练过程中引入Bayesian算法，在修正各层间连接权值的同时自动修正网络的超参数。

最后，通过缺陷量化试验，对所提出的量化人工神经网络的训练时间、缺陷量化精度及抗干扰能力等性能进行验证。

1.基于RBF人工神经网络的缺陷分类方法

在人工神经网络模型中，单个神经元只能实现从输入信号到输出信号的线性变换。在基于人工神经网络对缺陷进行分类时，为了实现输入数据与输出数据之间的非线性映射，采用了RBF人工神经网络。RBF人工神经网络以径向基函数作为传递函数，完成输入数据从非线性空间到线性空间的映射，再根据权值进行线性变换，得到最终的输出数据。在隐含层神经元足够多的前提下，这种将数据从非线性空间转换到线性空间的变换，可实现对漏磁检测缺陷的分类。

在RBF人工神经网络的结构中，输入层与隐含层之间不存在权值连接，仅通过径向基函数进行信息传递，而隐含层与输出层之间依靠权值进行信息传递。设I=（I₁，…，I_m）为该人工神经网络的输入向量，O为输出信号，φ=（φ₁，…，φ_m）为连接输入层与隐含层的径向基函数，c=（c₁，…，c_m）为径向基函数的中心，w=（w₁，…，w_m）为连接该人工神经网络隐含层与输出层的权值，n为隐含层所包含的神经元个数，θ为常数，则可计算得到RBF人工神经网络的输出函数为

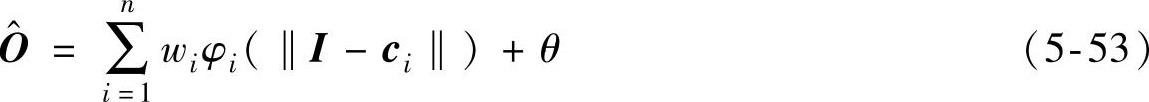
选择式（5-28）所示的高斯函数作为径向基函数，即

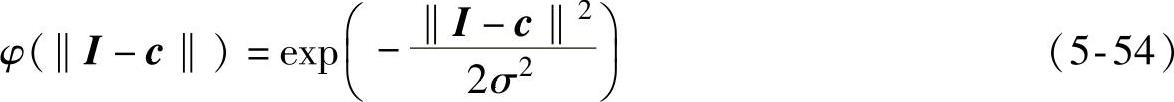
其中，σ为高斯函数的标准差。所选的高斯函数具有如下特点：在节点中心处的函数值很大，在远离中心处的函数值迅速下降。

在对RBF人工神经网络进行训练时，通过调整权值w、径向基函数的中心c和标准差σ来减小该人工神经网络实际输出值与目标输出值之间的差距。以均方误差作为人工神经网络训练过程中的目标函数，即

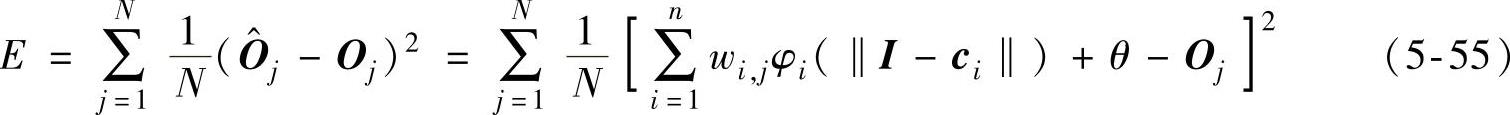
在RBF人工神经网络的训练过程中，基于最速下降算法对权值、径向基函数的中心与标准差进行修正。由此得到人工神经网络训练过程中第L个输出信号所对应的网络参数的改变量为

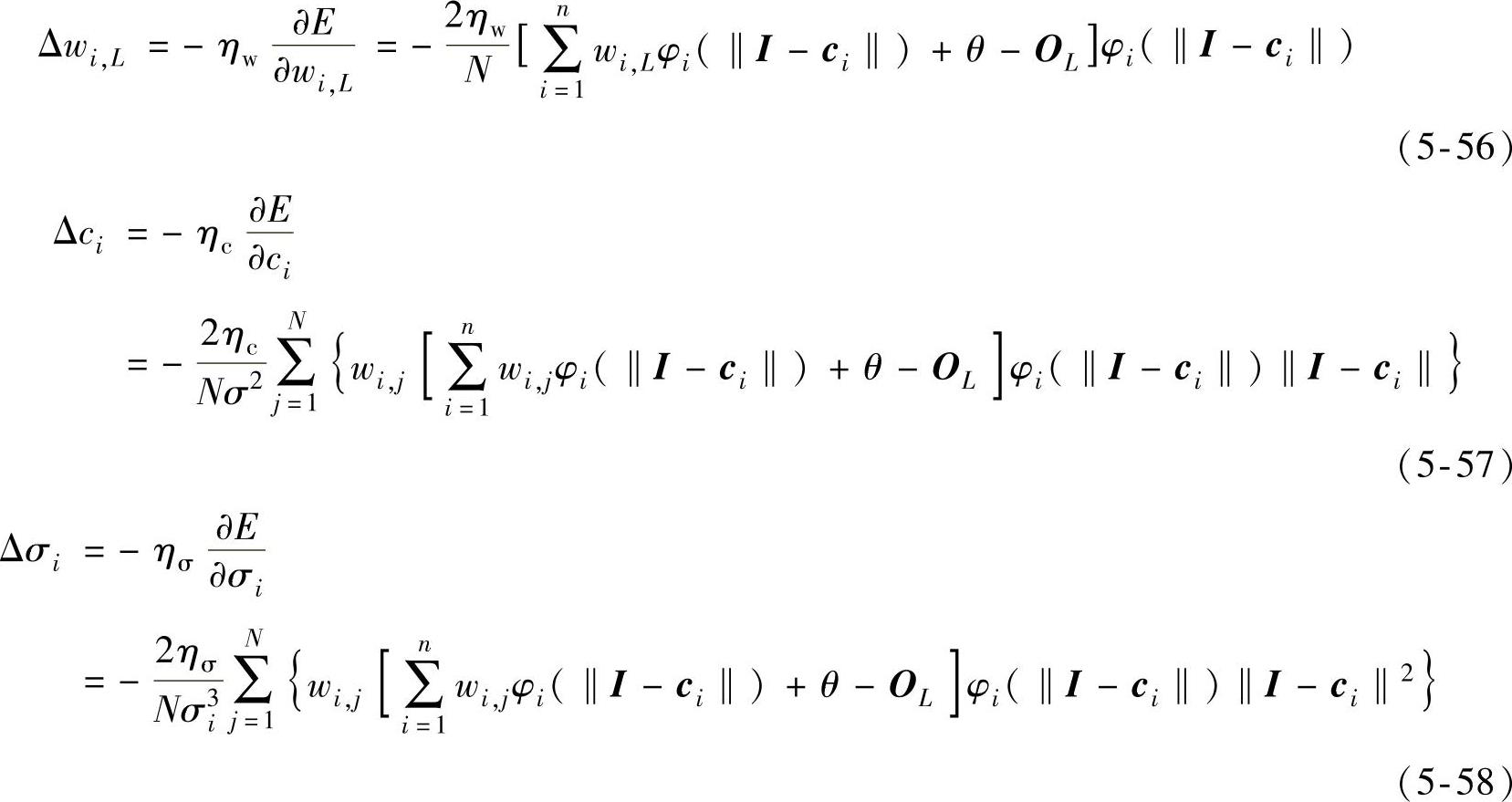
其中，η_w、η_c、η_σ为该人工神经网络中各个参数的学习速率，用于自适应地调整网络参数、修正算法的步长。学习速率过小，会导致网络的收敛速度较慢，且网络的训练时间过长；学习速率过大，网络训练过程中可能产生震荡，导致网络的稳定性较差。

根据前述缺陷分类标准，所训练的RBF人工神经网络的分类对象包含凹坑缺陷、水平沟槽缺陷、切向沟槽缺陷三种。图5-81给出了这三类缺陷的三维漏磁信号水平分量的示例。在5.2.1节中已指出，三类缺陷水平方向漏磁信号的特征具有明显的差异，因此，在对这三类缺陷进行分类时，可以只采用其水平方向漏磁信号的特征作为人工神经网络的输入信号。

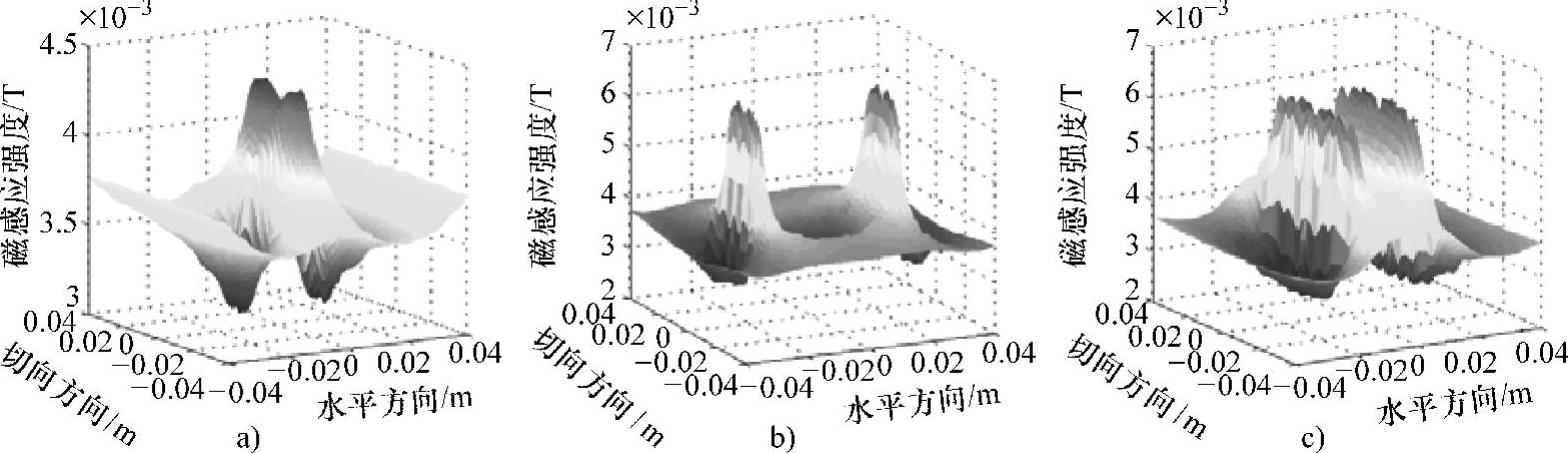
图5-81 三类缺陷三维漏磁信号水平分量

a）凹坑缺陷 b）水平沟槽缺陷 c）切向沟槽缺陷

由图5-81可以看出，凹坑、水平沟槽、切向沟槽三种类型缺陷的水平方向漏磁信号之间存在较大的差异。在选择RBF人工神经网络的输入信号时，通过提取特征量值的方法，难以获得统一的、能够准确反映缺陷种类的特征量值。因此，针对水平方向的漏磁信号，提出了一种网格平均处理方法，用于提取RBF分类网络的输入信号。

按照所提出的网格平均处理方法，需要对待处理的信号进行网格划分，并计算各网格内的信号平均值作为该网格的值。图5-82给出了凹坑、水平沟槽、切向沟槽三类缺陷的水平方向漏磁信号在进行网格平均处理后的结果。

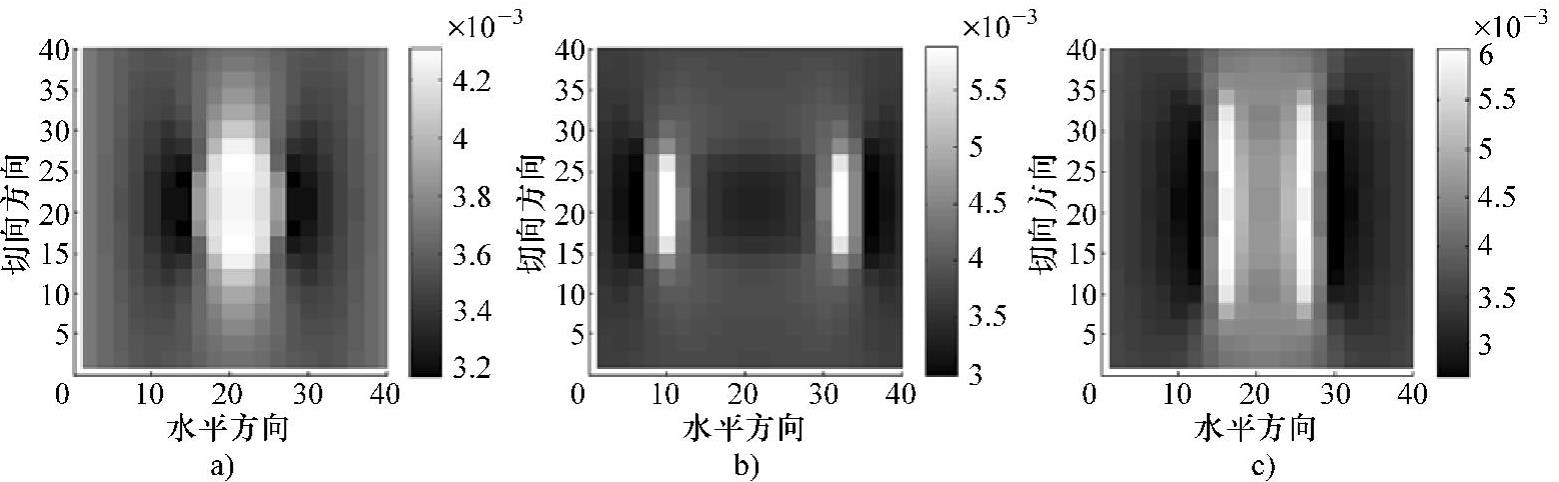
图5-82 水平方向漏磁信号的网格平均处理结果

a）凹坑缺陷 b）水平沟槽缺陷 c）切向沟槽缺陷

采用所提出的网格处理方法对缺陷的水平方向漏磁信号进行处理，可在保留信号主要特征的前提下，降低信号中的数据量。由图5-82可以看出，三种类型缺陷网格峰值集中区域之间的差异较大。因此，按照网格值的大小，提取网格值最大的20个网格位置，作为RBF人工神经网络的输入信号。

建立包含90个凹坑缺陷、150个水平沟槽缺陷、150个切向沟槽缺陷的缺陷样本库，分别选取70个凹坑缺陷、70个水平沟槽缺陷和70个切向沟槽缺陷作为人工神经网络的训练样本。另外，分别选取20个凹坑缺陷、20个水平沟槽缺陷和20个切向沟槽缺陷作为测试样本，用于对人工神经网络的分类准确度进行测试。

以提取的网格位置作为RBF人工神经网络的输入信号，以[1，0，0]、[0，1，0]、[0，0，1]代表凹坑缺陷、水平沟槽缺陷、切向沟槽缺陷，并将其作为所构建RBF人工神经网络的输出信号。将RBF人工神经网络训练的目标误差设置为0.001，当训练结果满足预先设定好的目标误差时，即完成对RBF人工神经网络的训练。

图5-83给出了RBF人工神经网络的训练过程曲线。由图可知，经过4556次训练，所构建的RBF人工神经网络达到了预先设定的精度要求。

以60个缺陷测试样本对所训练的分类网络进行验证，表5-27给出了其中6个测试样本的缺陷分类结果（包含测试样本中3个分类错误的样本）。

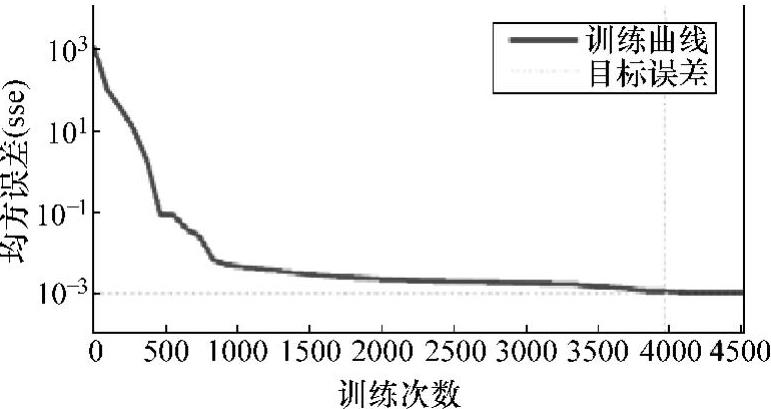
图5-83 RBF人工神经网络训练过程曲线

表5-27 6个测试样本的缺陷分类结果

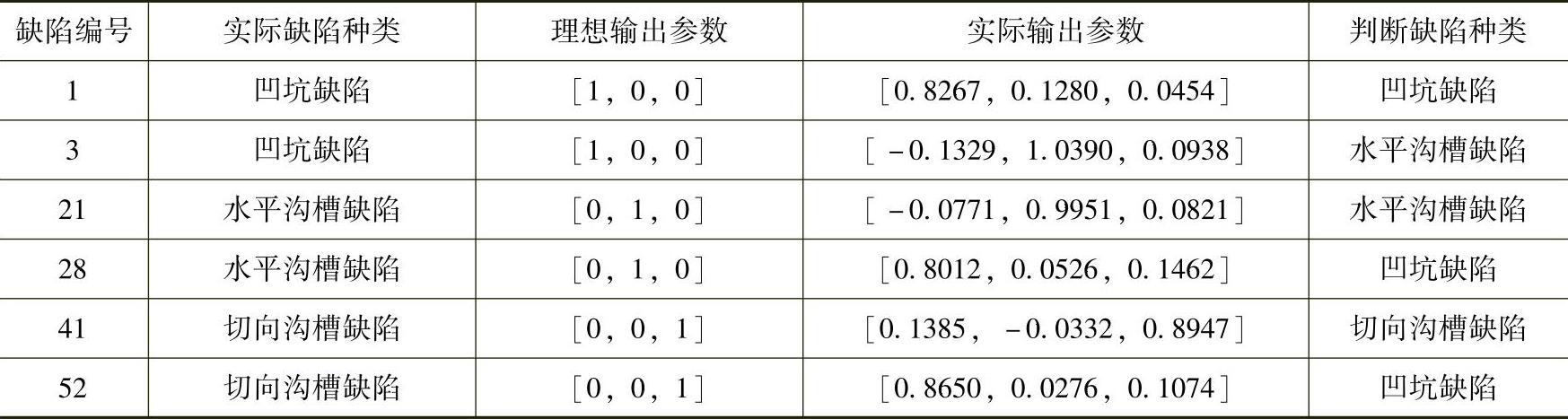
以测试样本1的缺陷分类结果为例，RBF人工神经网络的实际输出为[0.8267，0.1280，0.0454]，对其进行四舍五入后，得到缺陷分类的近似结果[1，0，0]，据此，该缺陷的分类为凹坑缺陷。对测试样本28进行同样的分类判断，该缺陷实际为水平沟槽缺陷，然而其缺陷分类的结果为凹坑缺陷，说明网络分类出现了错误。

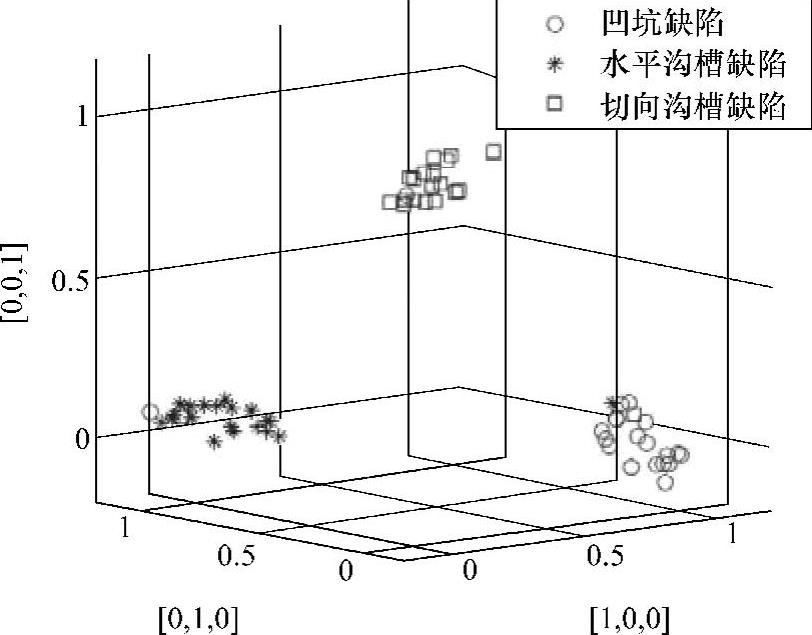
图5-84 60个测试样本的缺陷分类结果

图5-84所示为全部60个测试样本的缺陷分类结果。由图可知，在60个测试样本缺陷中，共有5个样本的分类结果错误，分类的正确率为91.7%。这表明训练得到的RBF人工神经网络可实现对三类缺陷的分类。

2.基于BP人工神经网络的缺陷量化方法

BP人工神经网络具有较强的非线性映射能力，在具有足够多神经元的前提下，BP人工神经网络可以无限逼近任意的非线性函数，因此可用于建立缺陷三维漏磁信号特征量值与缺陷几何尺寸之间的非线性映射关系。

在BP人工神经网络中，以I=（I₁，…，I_m）表示输入信号，以O=（O₁，…，O_n）表示输出信号，用D=（I，O）代表训练样本集，以w₁表示连接输入层与隐含层的权值，用w₂表示连接隐含层与输出层的权值，以W=（w₁，w₂）表示整体权值，并以p表示隐含层所包含的神经元个数，则可计算得到BP人工神经网络的输出函数为

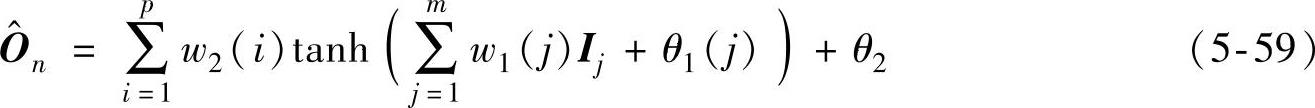
基于误差最小原则对BP人工神经网络进行训练，即通过减小实际输出值与目标输出值之间的误差，对其中的权值进行调整。据此，可得到BP人工神经网络训练过程中的目标函数，即

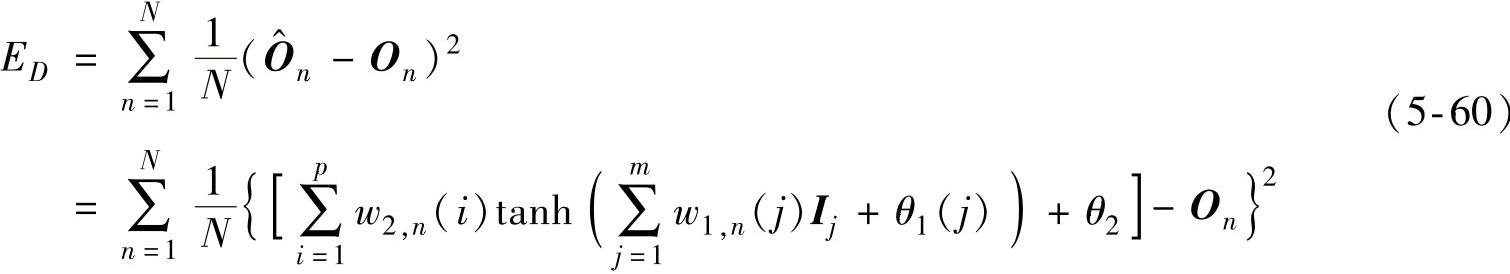
在BP人工神经网络的训练过程中，常用最速下降法来优化权值，即求取式（5-60）的极小值。由此得到训练过程中第L个输出信号所对应权值的改变量，即

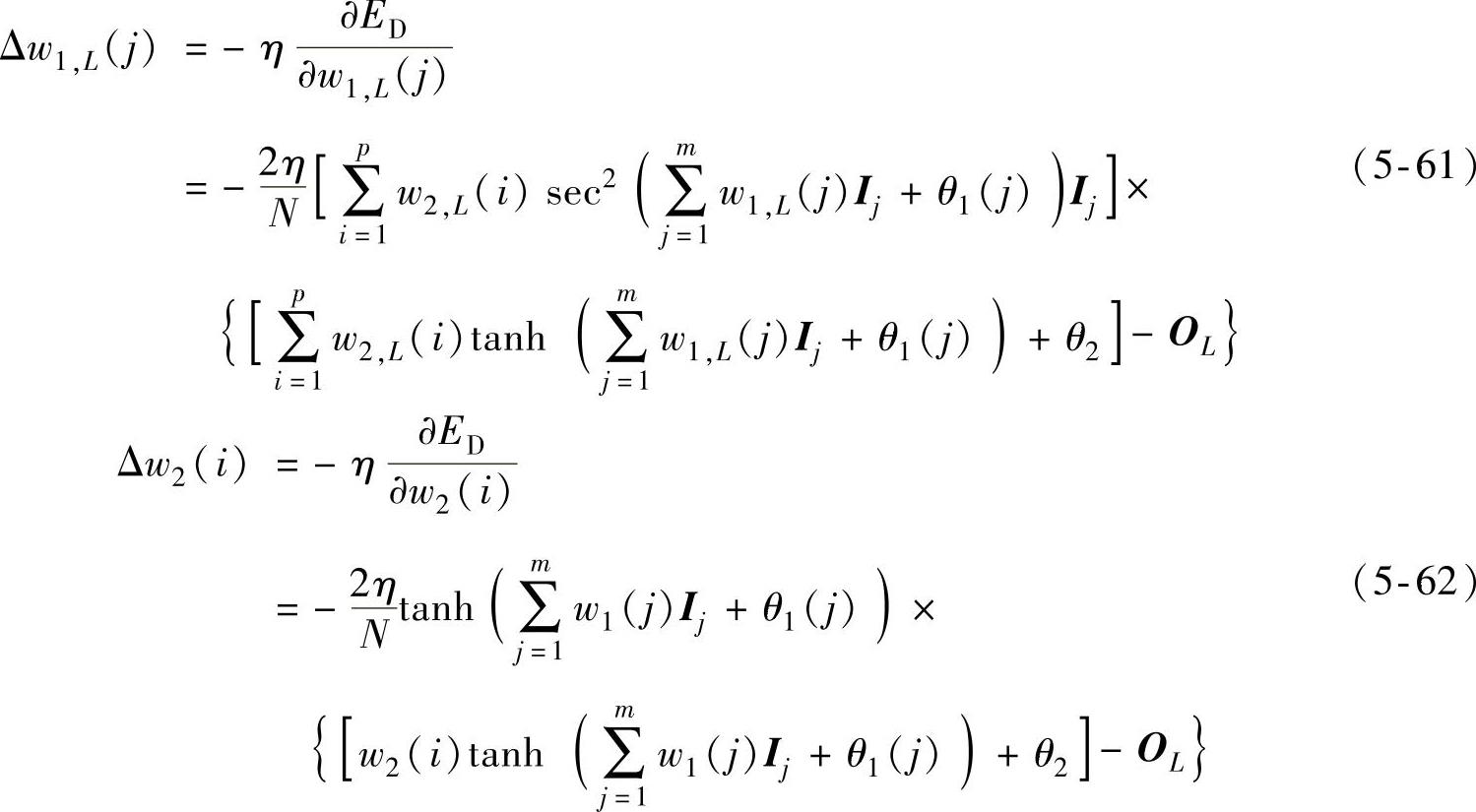
其中，η为权值修正过程的学习速率，用于在梯度下降算法中调整权值的修正步长。

采用以上模型对BP人工神经网络的权值进行修正时，需要预先设定隐含层神经元的数目。如果神经元数目过多，会导致该人工神经网络复杂度高、泛化能力差。但如果神经元数目过少，则会导致该人工神经网络的非线性拟合度较差。为了将神经元数目调整到合适的值，从而减少其对该人工神经网络造成的不良影响，在该人工神经网络的训练中，在目标函数的基础上增加了衰减函数，即

通过控制式（5-63）的取值大小，可有效地控制该人工神经网络的复杂度。因此，可得到该人工神经网络训练的最终目标函数为

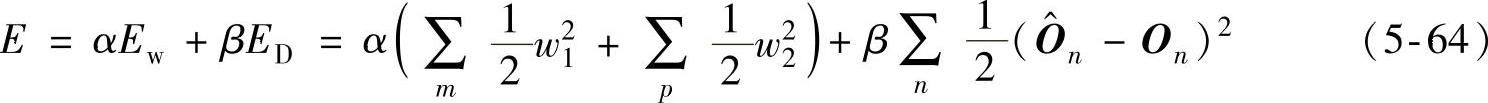
式中，α和β为超参数，用于对网络的复杂度进行调整。

若α＞＞β，则说明训练目标为尽可能减小实际输出值与目标输出值之间的误差，对网络规模的控制较少，导致该人工神经网络出现了过度拟合；若α＜＜β，则说明训练目标为尽可能减小网络的复杂度，会导致该人工神经网络的非线性拟合能力较差。

采用最速下降算法对该人工神经网络进行优化时，无法实现对超参数α、β的调整。因此，将Bayesian算法引入BP人工神经网络的优化过程，在训练过程中实现超参数的自适应调整，从而在该人工神经网络的误差与该人工神经网络的规模之间取得平衡。

Bayesian算法是一种常用的对参数范围进行估计的方法，其本质是：利用事件在过去的出现概率，对事件在未来的出现概率进行预测，即利用先验概率分布来求解后验概率分布。根据Bayesian定理，任意待求量均可被看作随机变量，能通过概率分布对其进行描述。Bayesian定理通过Bayesian公式进行表达，即

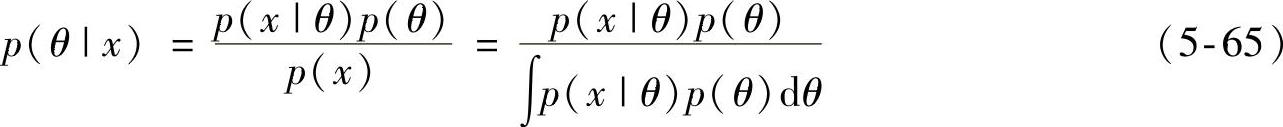
式中，θ为待求的随机变量；x为样本；p（θ|x）为θ的后验分布信息，即待求随机变量的分布信息；p（θ）代表θ的先验分布信息，即待求随机变量所拥有的初始概率；p（x）是样本x的边缘分布，通常被视为不依赖于变量θ的归一化因子。

由式（5-65）可知，Bayesian算法是通过待求随机变量的先验分布信息与样本的分布概率对变量的后验分布信息进行求解的。由于p（x）为归一化因子，故Bayesian定理的公式可等价为

p（θ|x）∝p（x|θ）p（θ） （5-66）

由式（5-66）可知，待求量θ的后验分布反映了抽样以后对随机变量θ的认识，即抽样信息对先验分布产生影响后的结果。

基于Bayesian算法的BP人工神经网络，通过Bayesian算法对人工神经网络的权值进行调整。其具体操作流程为：将人工神经网络中的所有参数看作随机变量，基于目标参数的先验概率分布与实际输入、输出信号的样本数据，对人工神经网络的权值范围做进一步修正，并通过对BP人工神经网络模型复杂度的控制，节约人工神经网络的训练时间、降低人工神经网络过度拟合的可能性、提高BP人工神经网络的泛化能力。

以A表示人工神经网络，根据Bayesian定理，采用无样本数据时人工神经网络权值的先验分布p（w|α，A），对有样本D=（I_m，O_n）后人工神经网络权值的后验分布p（w|D，α，β，A）进行估计。得到人工神经网络权值的后验概率分布函数为

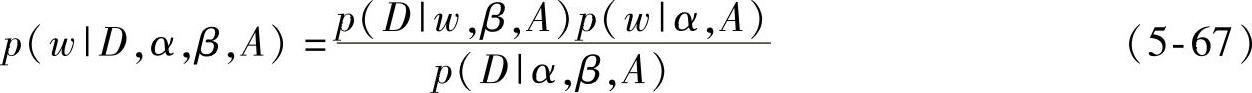
其中，p（D|w，β，A）为似然函数，即样本的联合分布。

p（D|α，β，A）为归一化因子，有

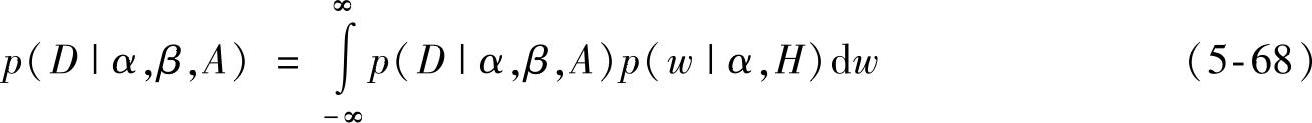
将人工神经网络样本的分布看作一个均值为零、方差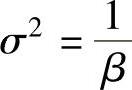的高斯分布，则可得到似然函数为

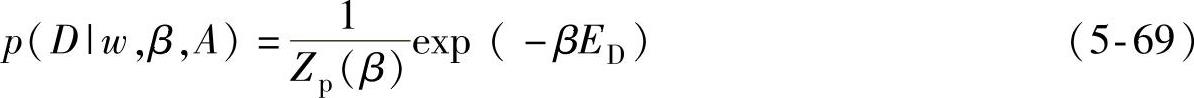
在式（5-69）中，Z_p（β）为归一化因子，可写成

同理，假设人工神经网络权值的分布是一个均值为零、方差σ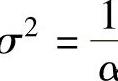α的高斯分布，则可得到人工神经网络权值的先验分布，即

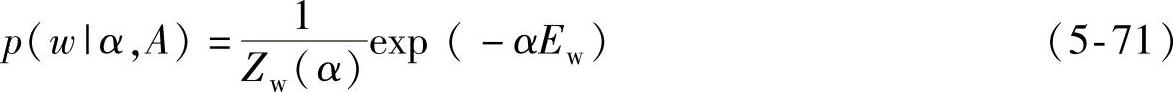
在式（5-71）中，Z_w（α）为归一化因子，可写成

根据式（5-67）、式（5-69）和式（5-71），可得到人工神经网络权值的后验概率分布函数为

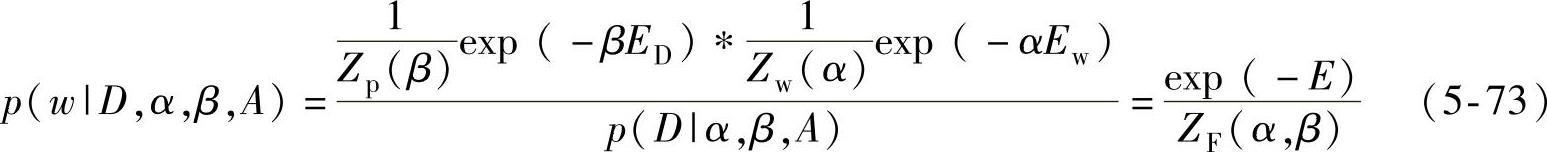
在以上框架下，对目标函数E做最小化处理，即可得到最可能的人工神经网络权值参数w。(www.xing528.com)

在人工神经网络权值w给定的前提下，可以对人工神经网络的超参数α、β的后验概率分布进行估计。根据Bayesian定理，得到超参数的后验概率分布为

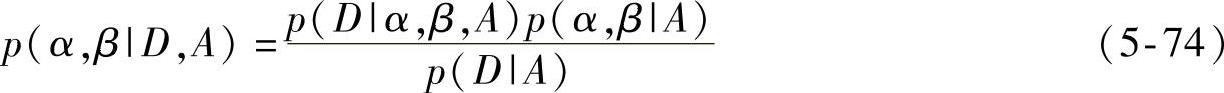
根据式（5-73）和式（5-74），归一化因子p（D|α，β，A）可写成

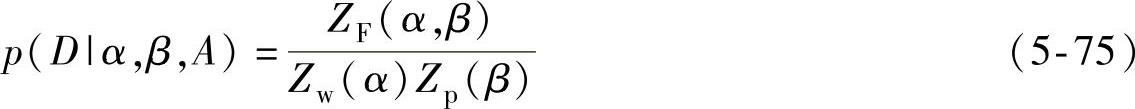
目标函数E在网络参数w处进行泰勒展开，并以此对目标函数进行最小化，从而得到使目标函数最小的人工神经网络权值w_MP，并基于此求得可能性最大的超参数α、β，即

其中，γ可通过人工神经网络的有效参数来表示。

综合以上分析，得到基于Bayesian算法的BP人工神经网络的训练流程，如图5-85所示。

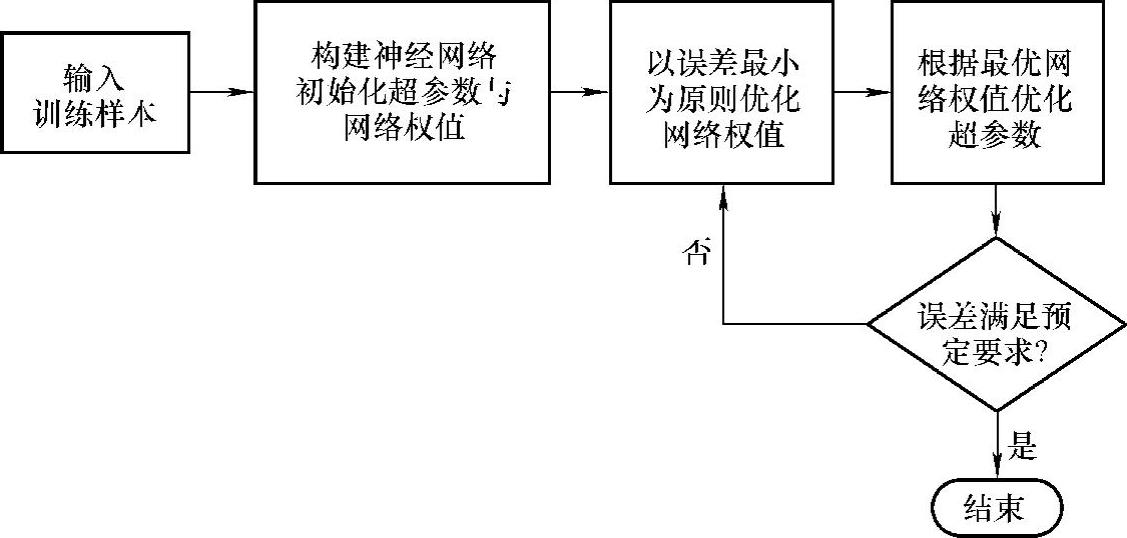
图5-85 基于Bayesian算法的BP人工神经网络训练流程

具体的BP人工神经网络训练过程如下：

1）将训练样本D=（I_m，O_n）输入到人工神经网络中。

2）给定初始人工神经网络结构，初始化人工神经网络的超参数α、β，初始化BP人工神经网络的权值w。

3）以误差最小为原则，最小化人工神经网络目标函数E，计算得到最优的BP人工神经网络权值w。

4）在最优网络权值w的基础上，计算最优的网络超参数α、β。

5）若BP人工神经网络优化函数E满足设定的误差要求，则结束人工神经网络的训练过程，得到训练好的人工神经网络；若优化函数E不满足设定的误差要求，且人工神经网络训练次数仍未达到上限，则重复步骤3），直至优化函数E满足要求，得到符合期望的人工神经网络；若人工神经网络训练次数已达到上限，但优化函数E仍不满足误差要求，则表明当前的人工神经网络不收敛。

根据以上的BP人工神经网络训练流程，可以构建缺陷几何尺寸信息与缺陷三维漏磁信号特征量值之间的非线性映射关系。

为了验证基于Bayesian算法的BP人工神经网络在减少人工神经网络训练时间上的有效性，以及其用于缺陷量化时的量化精度，需要进行对应的缺陷量化试验。首先，构建基于Bayesian算法的BP人工神经网络，采用缺陷三维漏磁信号关键特征量值作为BP人工神经网络的输入信号，采用缺陷几何尺寸作为BP人工神经网络的输出信号，得到缺陷三维漏磁信号关键特征量值与缺陷几何尺寸之间的映射关系。进而比较引入Bayesian算法对网络进行优化前后的网络训练时间，并采用测试数据验证所训练人工神经网络的量化精度与抗干扰能力。

针对凹坑缺陷，利用包含90个缺陷的缺陷样本库，提取样本库内缺陷三维漏磁信号的关键特征量值。从这些缺陷样本中，选择79组用于人工神经网络的训练，剩余11组样本将作为测试数据，用于对训练好的人工神经网络的量化精度进行验证。

以0.001作为人工神经网络训练的目标均方误差，图5-86和图5-87分别给出了对凹坑缺陷直径和凹坑缺陷深度进行量化的人工神经网络训练过程。其中，图5-86a与图5-87a所示为基于传统的BP人工神经网络，采用缺陷三维漏磁信号的关键特征量值对缺陷的直径、深度进行量化。图5-86b与图5-87b所示为基于Bayesian算法的BP人工神经网络，采用缺陷一维漏磁信号的关键特征量值对缺陷直径、深度进行量化。图5-86c与图5-87c则给出了基于Bayesian算法的BP人工神经网络，采用缺陷三维漏磁信号特征量值对缺陷直径、深度进行量化的网络训练过程。在各个训练过程图中，均用虚线标出了人工神经网络训练的目标误差。

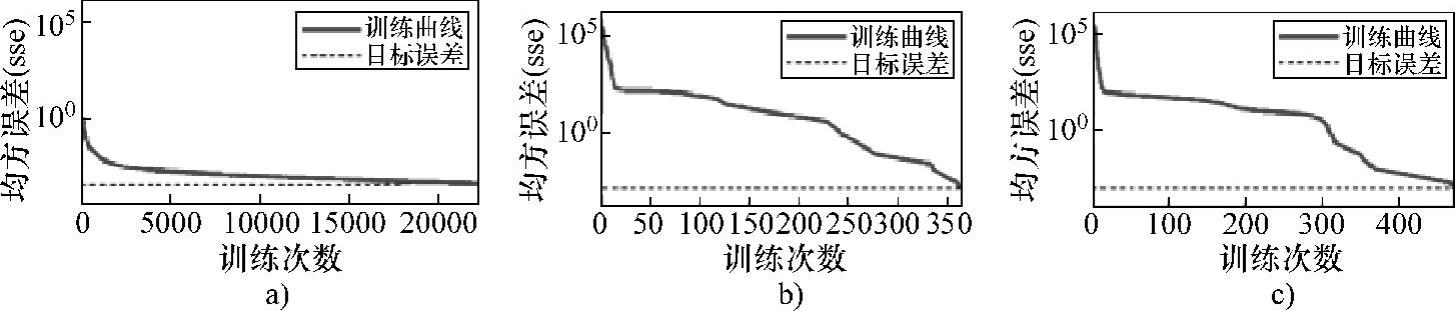
图5-86 凹坑缺陷直径量化人工神经网络的训练过程

a）三维漏磁信号、传统算法 b）一维漏磁信号、Bayesian算法 c）三维漏磁信号、Bayesian算法

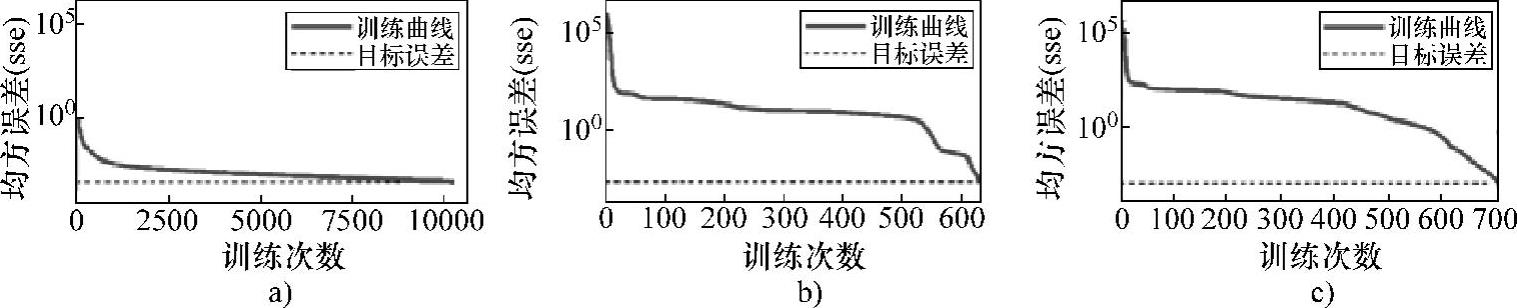
图5-87 凹坑缺陷深度量化人工神经网络训练过程

a）三维漏磁信号、传统算法 b）一维漏磁信号、Bayesian算法 c）三维漏磁信号、Bayesian算法

对比图5-86a与图5-86c可以看出，在采用缺陷三维漏磁信号特征量值对人工神经网络进行训练时，传统BP人工神经网络经过22598次训练达到了预期目标，而基于Bayesian算法的BP人工神经网络只需473次训练就达到了预期目标，其收敛速度更快，可有效地减少训练时间。而对比图5-86b与图5-86c可以看出，采用缺陷一维漏磁信号特征量值对人工神经网络进行训练时，经过365次训练达到了预期目标，比采用缺陷三维漏磁信号特征量值进行训练的次数要少，这与人工神经网络输入变量的减少是一致的。比较图5-87a与图5-87c、图5-87b与图5-87c，也可以得到相同的结论。以上结果表明，基于Bayesian算法的BP人工神经网络，相比于传统的BP人工神经网络，具有收敛速度快、训练时间短的优点。

针对凹坑缺陷，统计11个测试样本的缺陷直径与深度的量化结果，如图5-88所示。其中，横坐标代表11个缺陷样本的编号，纵坐标代表该缺陷尺寸的量化结果与缺陷实际几何尺寸的相对比例。表5-28给出了不同情况下针对凹坑缺陷量化结果的最大相对误差。

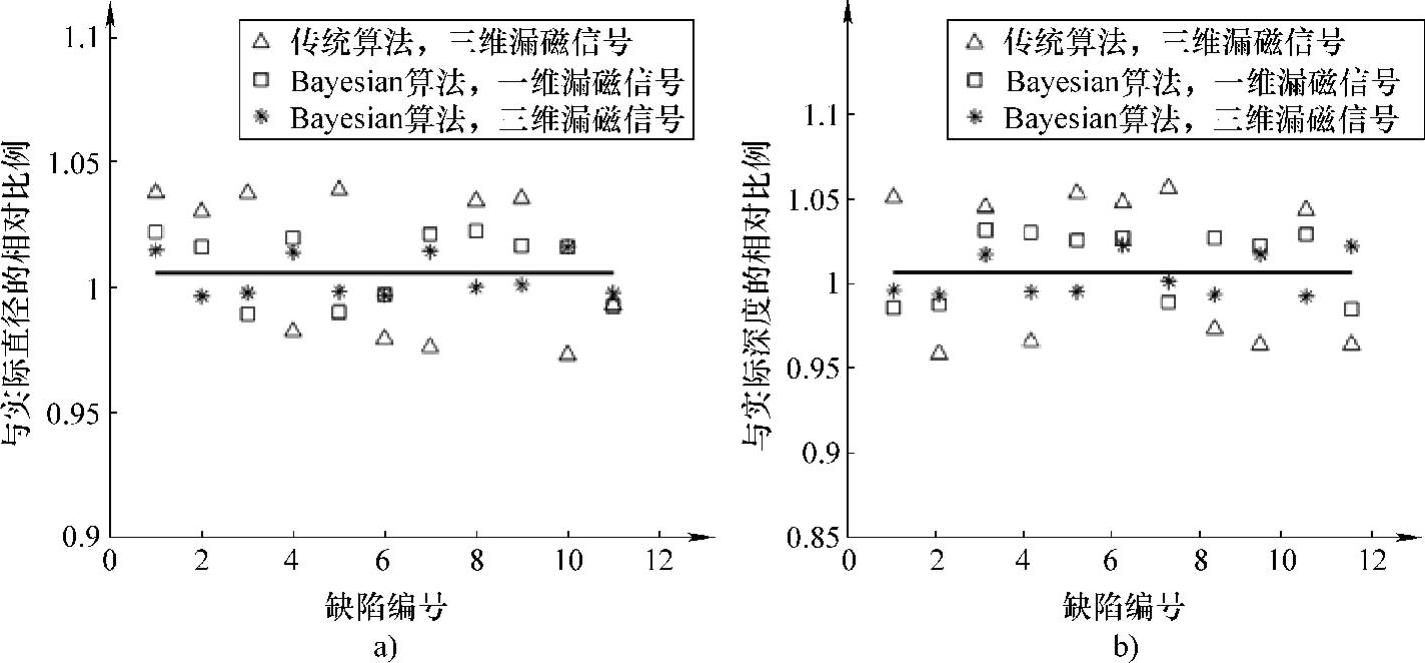
图5-88 凹坑缺陷量化结果与实际尺寸的相对比例

a）直径 b）深度

表5-28 凹坑缺陷量化的最大相对误差

从表5-28中给出的量化结果可以看出，在采用三维漏磁信号特征量值对缺陷进行量化时，使用传统BP人工神经网络对缺陷直径、深度量化的最大相对误差要大于基于Bayesian算法的BP人工神经网络量化的最大相对误差。从图5-88中也可以看出，在各测试样本的量化结果中，传统BP人工神经网络的量化误差普遍高于基于Bayesian算法的BP人工神经网络的量化误差。以上结果表明，基于Bayesian算法的BP人工神经网络可在缺陷三维漏磁信号的特征量值与缺陷几何尺寸之间建立更好的映射关系，能提高对凹坑缺陷的量化精度。

除此之外，在采用基于Bayesian算法的BP人工神经网络对缺陷进行量化时，使用三维漏磁信号对缺陷直径、深度量化的最大相对误差要小于使用一维漏磁信号进行量化的最大相对误差。在各测试样本的量化结果中也可看出，采用缺陷三维漏磁信号量化的相对误差普遍低于采用一维漏磁信号的量化误差。以上结果表明，缺陷三维漏磁信号包含更多的缺陷信息，采用三维漏磁信号对储罐底板缺陷进行量化能有效提高缺陷的量化精度。

针对水平沟槽缺陷，利用其包含150个缺陷的样本库，提取样本库内缺陷的三维漏磁信号的关键特征量值。在这些缺陷样本中，选择130组缺陷样本用于人工神经网络的训练，剩余20组样本用于对训练好的人工神经网络进行量化精度的验证。

以0.001作为网络训练的目标误差，图5-89、图5-90与图5-91分别给出了对水平沟槽缺陷长度、宽度、深度进行量化的人工神经网络的训练过程。图5-89a、图5-90a与图5_-91a所示为基于传统BP人工神经网络、采用缺陷三维漏磁信号特征量值进行量化的网络训练过程。图5-89b、图5-90b与图5-91b所示为基于Bayesian算法的BP人工神经网络、采用缺陷一维漏磁信号特征量值进行量化的网络训练过程。图5-89c、图5-90c与图5-91c所示为基于Bayesian算法的BP人工神经网络、采用缺陷三维漏磁信号特征量值进行量化的网络训练过程。图中均用虚线标出了网络训练的目标误差，即0.001。

图5-89 水平沟槽缺陷长度量化人工神经网络训练过程

a）三维漏磁信号、传统算法 b）一维漏磁信号、Bayesian算法 c）三维漏磁信号、Bayesian算法

图5-90 水平沟槽缺陷宽度量化人工神经网络训练过程

a）三维漏磁信号、传统算法 b）一维漏磁信号、Bayesian算法 c）三维漏磁信号、Bayesian算法

图5-91 水平沟槽缺陷深度量化人工神经网络训练过程

a）三维漏磁信号、传统算法 b）一维漏磁信号、Bayesian算法 c）三维漏磁信号、Bayesian算法

通过图5-89a与图5-89c、图5-90a与图5-90c、图5-91a与图5-91c，可以对比采用传统BP人工神经网络与基于Bayesian算法的BP人工神经网络的训练过程。在对缺陷长度、宽度、深度进行量化的人工神经网络的训练过程中，传统BP人工神经网络分别经过28931、14305、19625次训练可达到预期目标，基于Bayesian算法的BP人工神经网络只经过994、375、717次训练就达到了预期目标。这一结果验证了基于Bayesian算法的BP人工神经网络的收敛速度更快。

通过图5-89b与图5-89c、图5-90b与图5-90c、图5-91b与图5-91c，可以对比使用基于Bayesian算法的BP人工神经网络时，采用缺陷一维漏磁信号特征量值与采用缺陷三维漏磁信号特征量值的网络训练过程。可以看出，在对缺陷长度、宽度、深度进行量化的人工神经网络的训练过程中，采用缺陷一维漏磁信号特征量值的人工神经网络分别经过824、286、666次训练达到了预期目标，比采用缺陷三维漏磁信号特征量值进行训练的次数略少，与其采用了较少的漏磁信号特征量值相符。

针对水平沟槽缺陷，统计20个测试缺陷样本的长度、宽度、深度的量化结果，如图5-92所示。表5-29给出了水平沟槽缺陷尺寸量化结果的最大相对误差。

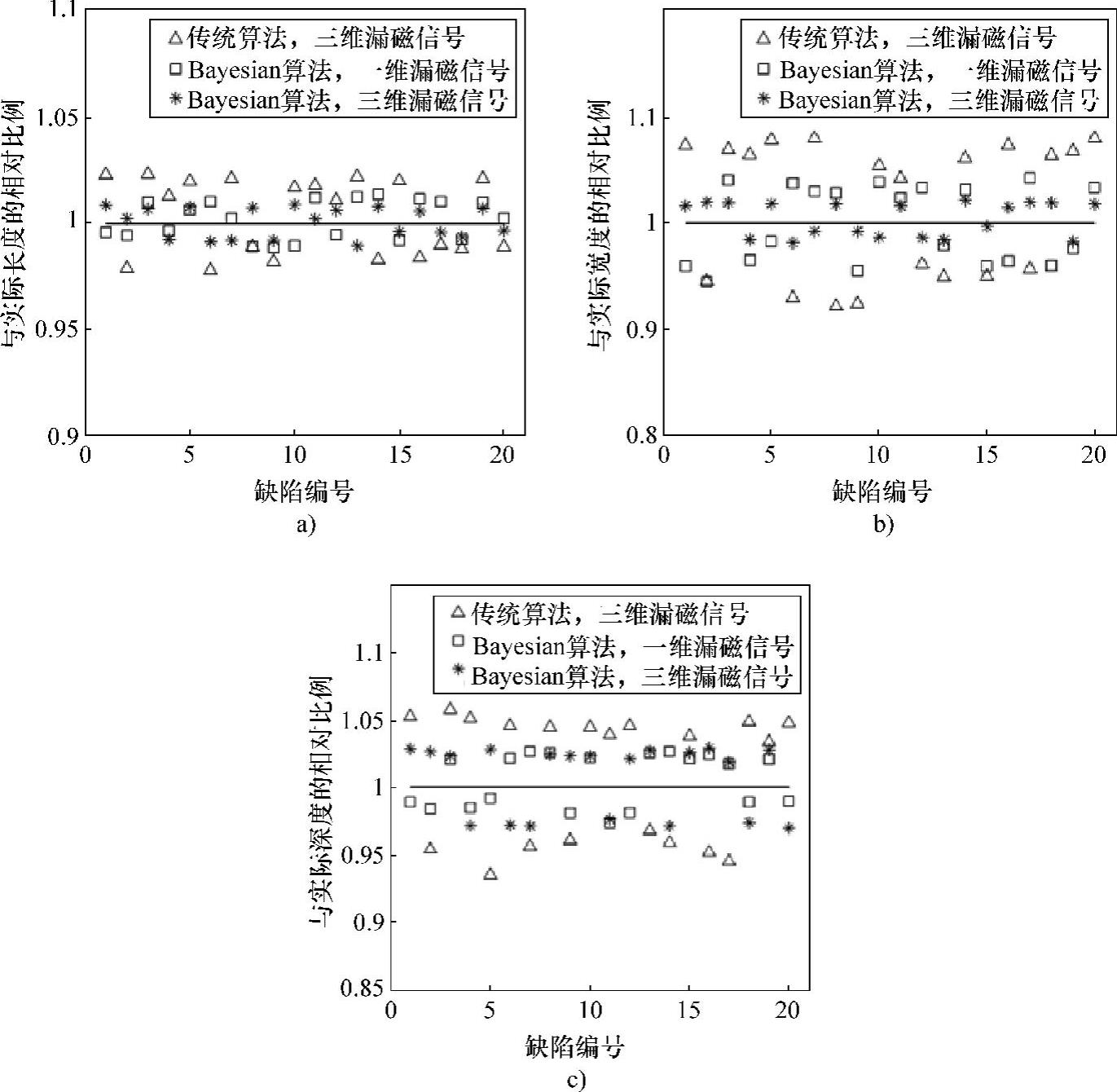
图5-92 水平沟槽缺陷量化结果与实际尺寸相对比例

a）长度 b）宽度 c）深度

表5-29 水平沟槽缺陷量化的最大相对误差

从表5-29中给出的量化结果可以看出，在采用三维漏磁信号对水平沟槽缺陷进行量化时，使用传统BP人工神经网络对缺陷长度、宽度、深度量化的最大相对误差要大于基于Bayesian算法的BP人工神经网络量化的最大相对误差。从图5-92中同样可以看出，在20个测试样本的量化结果中，传统BP人工神经网络的量化误差普遍高于基于Bayesian算法的BP人工神经网络的量化误差。由此可知，采用基于Bayesian算法的BP人工神经网络能有效地提高对储罐底板水平沟槽缺陷的量化精度。

由表5-29可知，在采用基于Bayesian算法的BP人工神经网络对水平沟槽缺陷进行量化时，使用缺陷三维漏磁信号进行量化的最大相对误差要小于使用一维漏磁信号进行量化的最大相对误差。并且在图5-92所示的量化结果中，采用三维漏磁信号对缺陷进行量化的相对误差普遍低于采用一维漏磁信号的量化误差。这是由于缺陷三维漏磁信号包含更多的缺陷信息，因而采用三维漏磁信号对储罐底板水平沟槽缺陷长度、宽度进行量化，能有效提高缺陷的量化精度。

在150个切向沟槽缺陷样本中，选择130组用于人工神经网络的训练，剩余20组用于验证训练好的人工神经网络的量化精度。

图5-93、图5-94与图5-95分别给出了针对切向沟槽缺陷长度、宽度、深度量化的网络训练过程。其中，图5-93a、图5-94a与图5-95a所示为基于传统BP人工神经网络、采用缺陷三维漏磁信号特征量值对缺陷进行量化的人工神经网络训练过程；图5-93b、图5-94b与图5-95b所示为基于Bayesian算法的BP人工神经网络、采用缺陷一维漏磁信号特征量值对缺陷进行量化的人工神经网络训练过程；图5-93c、图5-94c与图5-95c所示为基于Bayes_- ian算法的BP人工神经网络、采用缺陷三维漏磁信号特征量值对缺陷进行量化的人工神经网络训练过程。

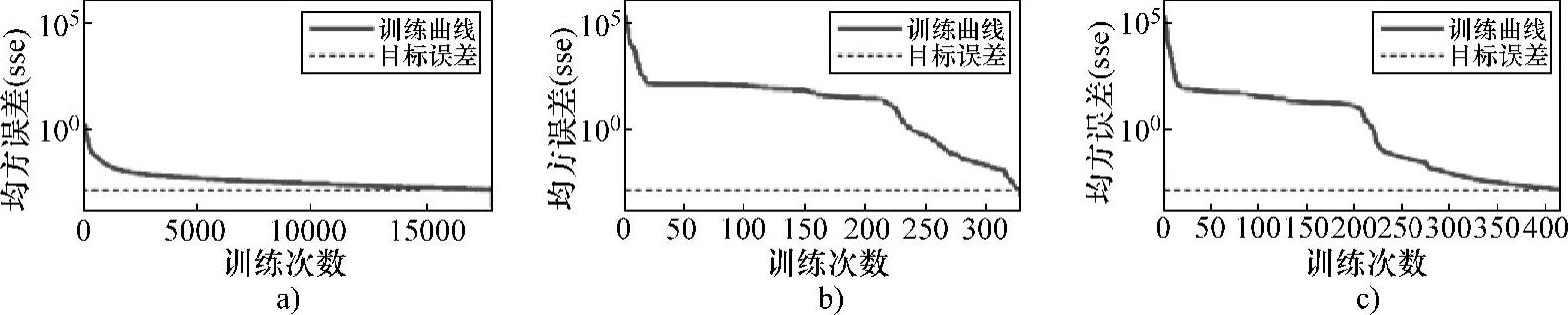
图5-93 切向沟槽缺陷长度量化人工神经网络训练过程

a）三维漏磁信号、传统算法 b）一维漏磁信号、Bayesian算法 c）三维漏磁信号、Bayesian算法

图5-94 切向沟槽缺陷宽度量化人工神经网络训练过程

a）三维漏磁信号、传统算法 b）一维漏磁信号、Bayesian算法 c）三维漏磁信号、Bayesian算法

图5-95 切向沟槽缺陷深度量化人工神经网络训练过程

a）三维漏磁信号、传统算法 b）一维漏磁信号、Bayesian算法 c）三维漏磁信号、Bayesian算法

基于图5-93a与图5-93c、图5-94a与图5-94c、图5-95a与图5-95c，可以对比采用缺陷三维漏磁信号特征量值时，分别使用传统BP人工神经网络与基于Bayesian算法的BP人工神经网络的网络训练次数。传统BP人工神经网络分别经过17882、9185、28652次训练达到了预期目标，而基于Bayesian算法的BP人工神经网络只经过416、269、779次训练就达到了预期目标，这进一步验证了基于Bayesian算法的BP人工神经网络具有较快的收敛速度。此外，从图5-93b、图5-94b与图5-95b可以看出，在切向沟槽缺陷的长度、宽度、深度量化人工神经网络的训练过程中，采用缺陷一维漏磁信号特征量值的人工神经网络训练，分别经过326、146、694次迭代后达到了预期目标，略少于图5-93c、图5-94c与图5-95c中采用缺陷三维漏磁信号特征量值时的训练次数。这也是由于缺陷三维漏磁信号的特征量值多于一维漏磁信号的特征量值，增加了网络的输入变量。

图5-96给出了切向沟槽缺陷的20个测试样本的长度、宽度、深度量化结果，其中横坐标代表20个缺陷的编号，纵坐标代表该缺陷长度、宽度、深度量化结果与缺陷实际几何尺寸的相对比例。表5-30统计了几种情况下切向沟槽缺陷量化结果的最大相对误差。

从图5-96与表5-30中给出的量化结果可以看出，与凹坑缺陷、水平沟槽缺陷的量化结果相似，采用传统BP人工神经网络对切向沟槽缺陷几何尺寸量化的误差要普遍高于基于Bayesian算法的BP人工神经网络量化的误差。验证了基于Bayesian算法的BP人工神经网络能有效地提高对切向沟槽缺陷的量化精度。

在采用基于Bayesian算法的BP人工神经网络对切向沟槽缺陷进行量化时，使用一维漏磁信号对缺陷长度、宽度的量化误差要高于采用三维漏磁信号的量化误差，验证了缺陷三维漏磁信号包含更多的缺陷信息，可以有效提高缺陷的量化精度。

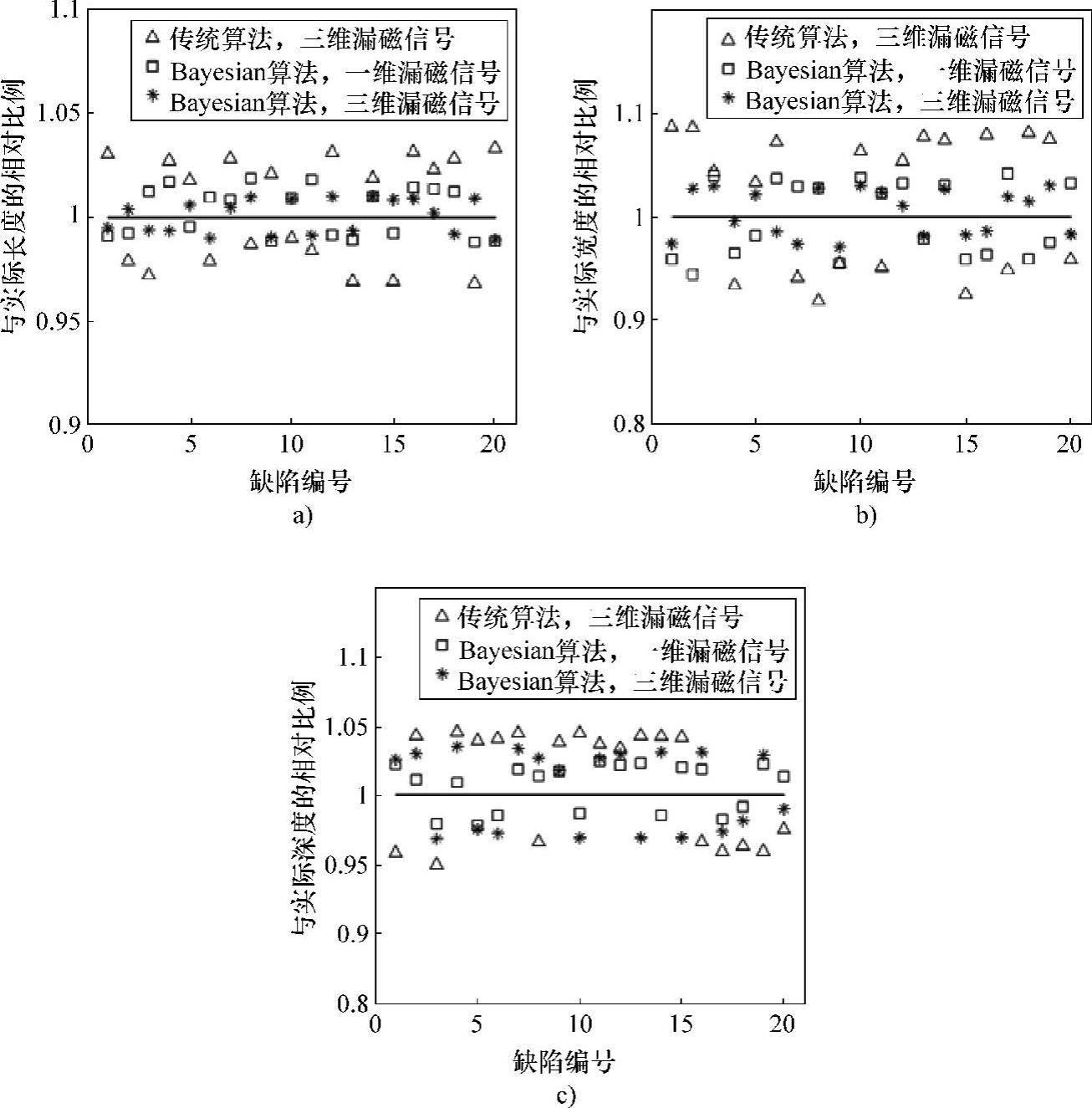
图5-96 切向沟槽缺陷量化结果与实际尺寸相对比例

a）长度 b）宽度 c）深度

表5-30 切向沟槽缺陷量化的最大相对误差