常规的基于人工神经网络的缺陷量化反演方法,直接利用训练后的人工神经网络对缺陷轮廓参数进行预测,可称作人工神经网络直接反演方法。人工神经网络直接反演方法存在多方面的问题,使其难以用于缺陷三维轮廓反演。首先,由于缺陷量化反演问题的病态性,直接反演方法不一定能收敛于全局最优解,导致其量化反演精度低。其次,该类方法对训练样本的依赖性高,对未知形状缺陷的泛化能力不足。最后,人工神经网络方法存在维数灾难问题。当人工神经网络被直接用于缺陷三维轮廓反演时,三维MFL检测信号和缺陷轮廓的复杂参数表示会引起神经元数量的剧增,进而导致网络训练时间急剧增加,甚至导致网络训练算法根本无法收敛。
为了利用人工神经网络的快速性,采用迭代法的思想,解决人工神经网络的反演精度低和泛化能力不足的问题,进而研究MFL检测缺陷三维轮廓的人工神经网络迭代反演方法。为了减少人工神经网络的神经元数量,应用主成分分析法提取能有效反映缺陷轮廓参数的MFL检测信号主要特征值,并建立适用于人工神经网络方法的缺陷三维轮廓条状模型。在此基础上,将建立矩形、圆柱、弧面三种样本缺陷的等价条状模型和用于缺陷三维MFL检测信号正向预测的人工神经网络。进而,将正向预测人工神经网络嵌入迭代循环,提出MFL检测缺陷三维轮廓的人工神经网络迭代反演方法,并推导基于梯度下降算法的条状模型参数迭代修正公式。
1.三维MFL检测信号的主要特征值提取
人工神经网络的神经元数量与输入数据的规模正相关,因此存在维数灾难问题。当三维MFL检测数据被直接用于缺陷三维轮廓反演时,大规模的检测数据会引起神经元数量的剧增,易导致网络训练时间急剧增加甚至无法训练。
为了减少人工神经网络的神经元数量从而降低其训练复杂度,对三维MFL检测信号的冗余度进行分析,进而定义三维MFL检测信号的特性值,并从中提取能有效反映缺陷轮廓参数的MFL检测信号主要特征值,从而实现消除数据冗余、降低输入数据规模、减少人工神经网络神经元数量的目的。
基于28.6mm×7.2mm弧面缺陷、28.6mm×7.2mm圆柱缺陷及28.6mm×14.3mm×7.2mm矩形缺陷,分析三维MFL检测信号的数据冗余度。其中,三维MFL检测信号的轴向与周向采样间隔均为1mm,三维MFL检测信号分量均以90×90的矩阵进行表示。

图5-47 28.6mm×7.2mm弧面缺陷的三维MFL检测信号
a)轴向分量 b)径向分量 c)周向分量
图5-47所示为28.6mm×7.2mm弧面缺陷的三维MFL检测信号。分别提取三维MFL检测信号分量各自的特征向量,将所得到的特征向量按所占比例由高到低排列,并统计各特征向量占比的累加结果,如图5-48所示。由统计结果可知,轴向分量和径向分量的三个主要特征向量的占比之和已达到95%,周向分量的6个主要特征向量的占比之和达到了95%。为了在减少数据冗余的同时保持尽可能高的准确度,设定特征向量的占比阈值为95%,则示例缺陷三维MFL检测信号的轴向分量与径向分量均可用各自的3个主要特征向量表示,周向分量则可用其6个主要特征向量表示。
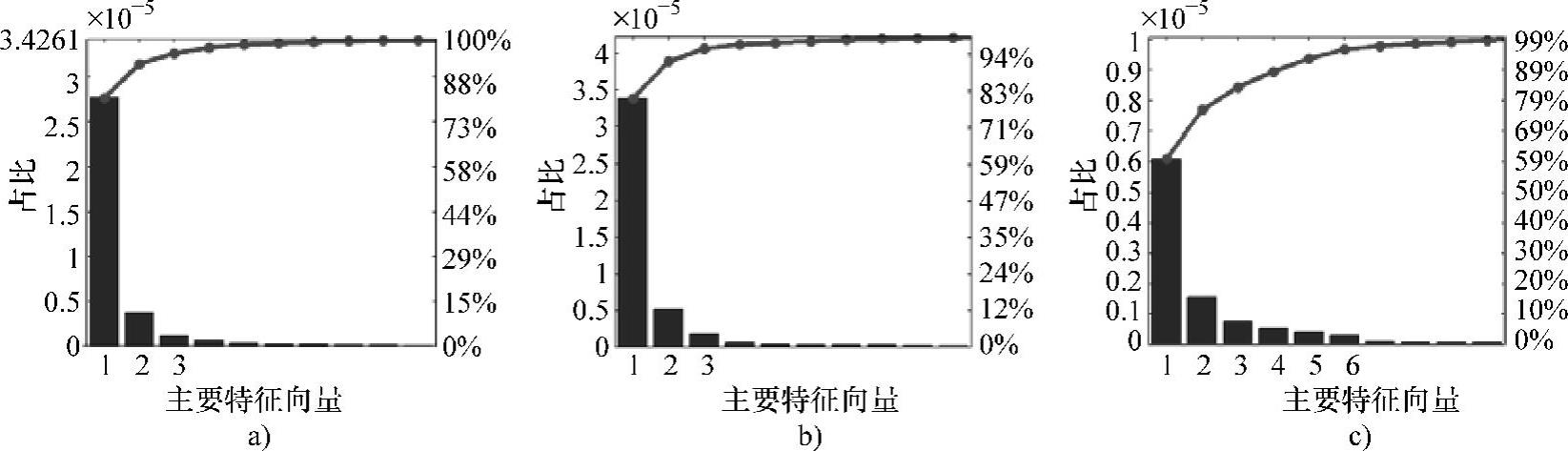
图5-48 28.6mm×7.2mm弧面缺陷三维MFL检测信号的主要特征向量占比及累加结果
a)轴向分量 b)径向分量 c)周向分量
因此,在保持原始三维MFL检测信号95%本征特点的精度下,轴向、径向与周向MFL检测信号可以分别使用90×3、90×3及90×6的矩阵进行简化表示。相比于原始的90×90矩阵,基于主要特征向量的简化表示分别减少了96.7%、96.7%和93.3%的待处理数据量。由此可知,原始三维MFL检测信号中存在大量的数据冗余。

图5-49 28.6mm×7.2mm圆柱缺陷三维MFL检测信号的主要特征向量占比及累加结果
a)轴向分量 b)径向分量 c)周向分量
以同样的方法,对28.6mm×7.2mm圆柱缺陷和28.6mm×14.3mm×7.2mm矩形缺陷的三维MFL检测信号进行分析,得到了如图5-49和图5-50所示的主要特征向量占比及累加结果。设定特征量占比阈值为95%,则圆柱缺陷三维MFL检测信号的轴向分量、径向分量与周向分量分别可用3个、3个和6个主要特征向量表示,矩形缺陷三维MFL检测信号的轴向分量、径向分量与周向分量分别可用3个、3个和5个主要特征量表示。采用主要特征向量对圆柱缺陷与矩形缺陷的MFL检测信号三维分量进行简化表示后,均可减少90%以上的待处理数据量,这表明原始三维MFL检测信号中存在大量的数据冗余。
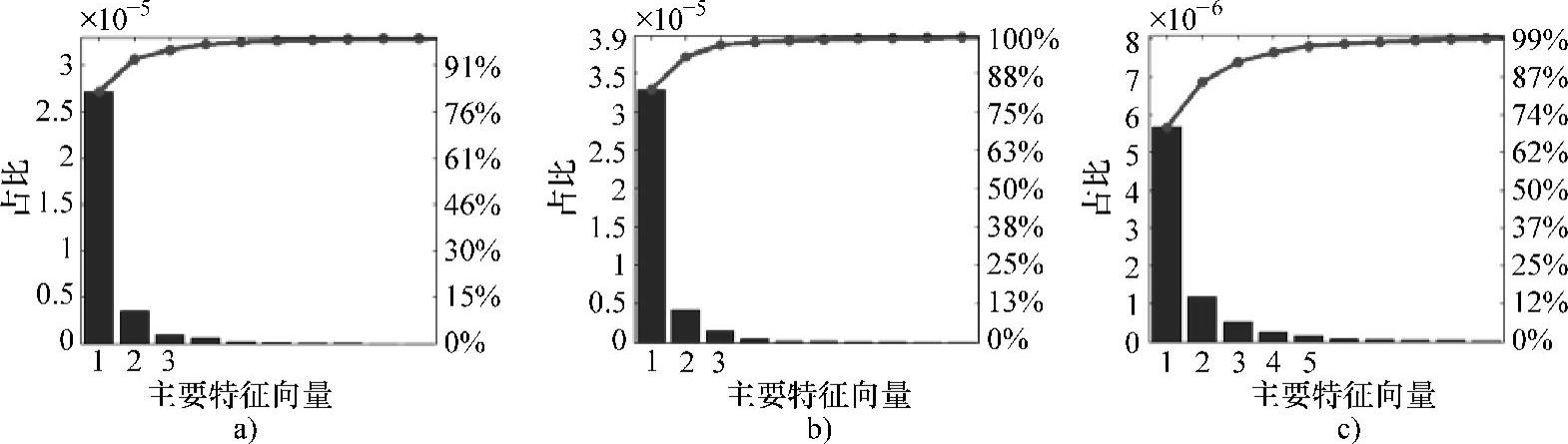
图5-50 28.6mm×14.3mm×7.2mm矩形缺陷三维MFL检测信号的主要特征向量占比及累加结果
a)轴向分量 b)径向分量 c)周向分量
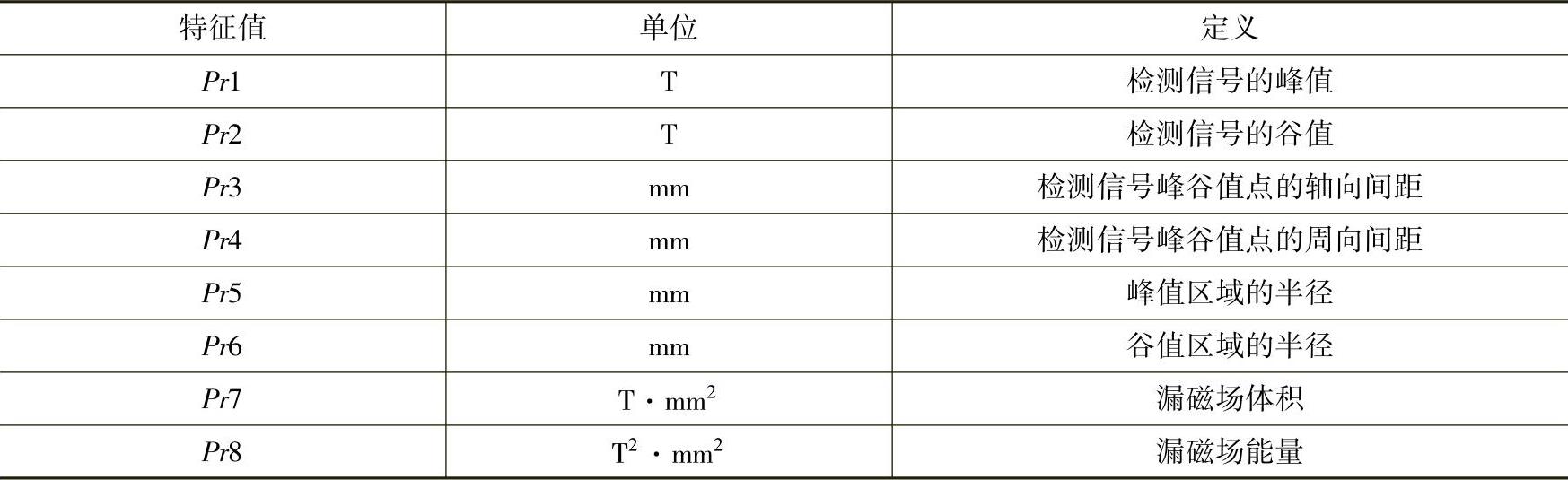
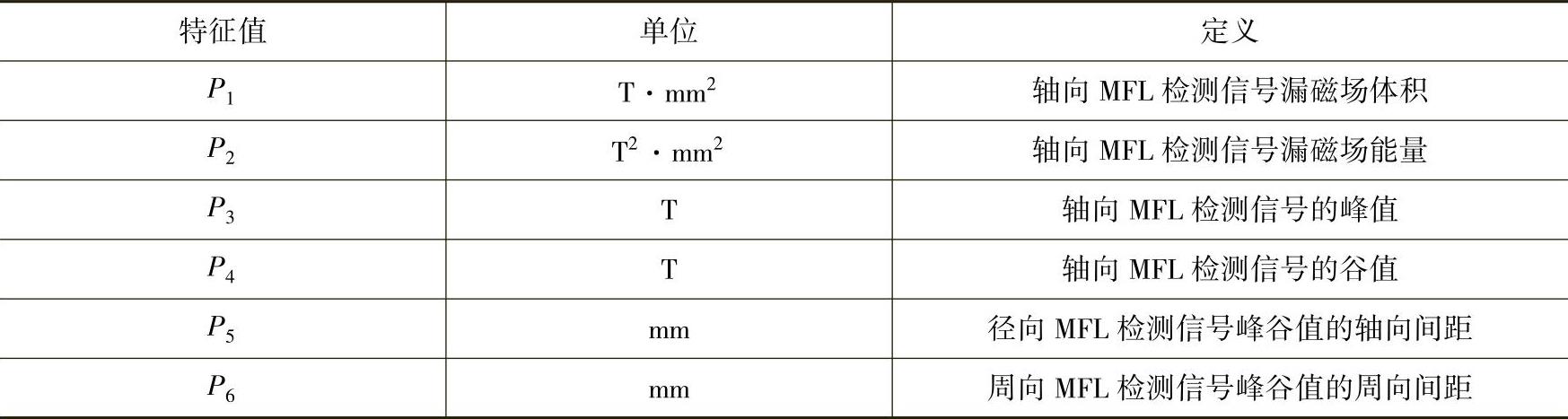
为了能准确反映缺陷的轮廓参数,对三维MFL检测信号的特征值进行定义。由于不同形状缺陷的三维MFL检测信号差别很大,特征值需要尽量选取一般缺陷所共有的一些基本特征。因此,在定义特征值时,考虑的内容主要包括三维MFL检测信号的峰谷值、峰谷值点的轴向与周向间距、漏磁场的“体积”与“能量”等反映缺陷开口轮廓或深度的基本特征。其中,漏磁场的“体积”为漏磁场磁感应强度的面积分,单位为T·mm2;漏磁场的“能量”为漏磁场磁感应强度平方的面积分,单位为T2·mm2。
以28.6mm×7.2mm弧面缺陷为例,对三维MFL检测信号的特征值进行定义。由于缺陷的轴向、径向和周向MFL检测信号各不相同,分别针对这三个分量进行特征值定义。
(1)轴向分量 图5-51所示为示例弧面缺陷的轴向MFL检测信号,该信号包含一个峰值区域(含两个峰值点)与两个谷值点。其中,两个谷值点分别位于缺陷沿轴向的左右开口处,峰值区域位于缺陷开口的中心。
首先,轴向信号的峰、谷值点反映了缺陷底部轮廓的拐点,因此将轴向MFL检测信号的峰、谷值及对应点的轴向与周向间距选作特征值。
其次,漏磁场轴向分量的整体幅值反映了缺陷深度的相对大小,因此选择轴向MFL检测信号的体积和能量作为特征值。此外,轴向MFL检测信号在缺陷开口边界处发生突变,因此将检测信号梯度最大值点的幅值与坐标选作特征值。
最后,考虑到轴向MFL检测信号中间峰值区域的复杂分布,分别沿轴向与周向取检测信号的中心检测曲线,如图5-52所示。在轴向中心检测曲线上,取峰谷值及对应的间距da作为特征值;在周向中心检测曲线上,取峰谷值及对应的间距dc作为特征值。

图5-51 28.6mm×7.2mm弧面缺陷的轴向MFL检测信号
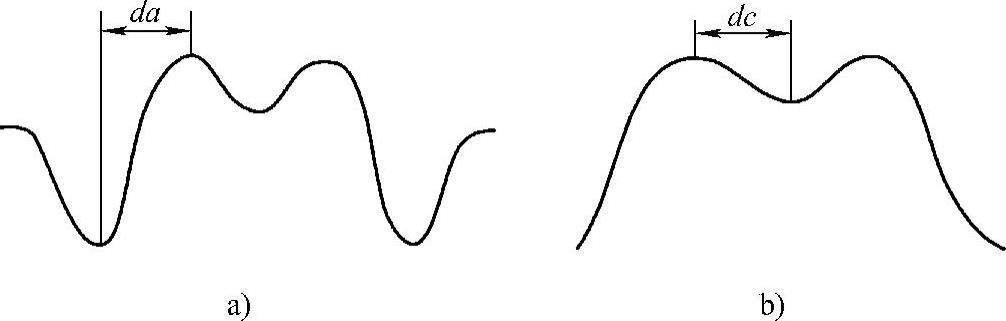
图5-52 轴向MFL检测信号中心检测曲线的特征值定义示意图
a)轴向中心检测曲线 b)周向中心检测曲线
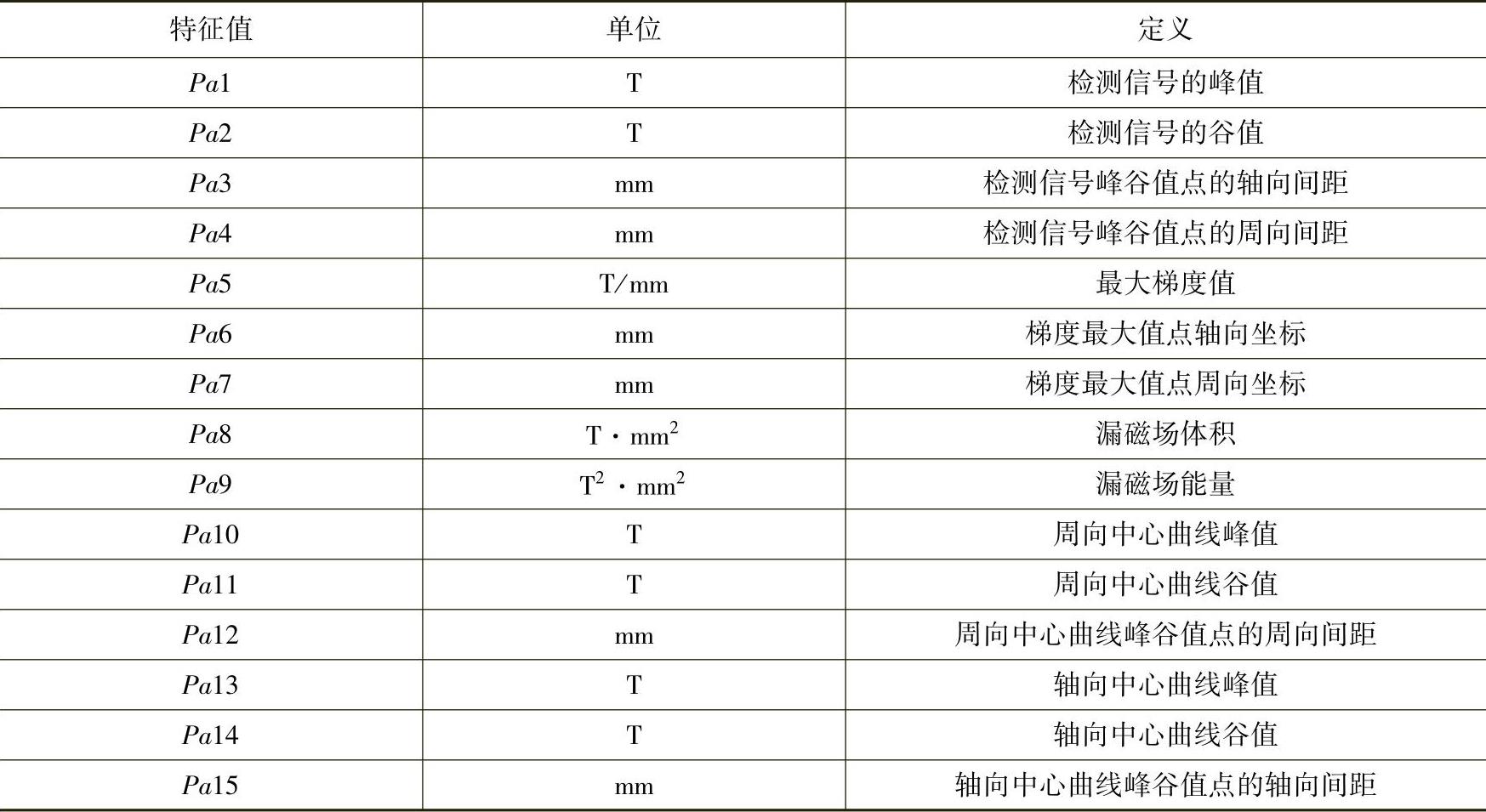
最终定义的轴向MFL检测信号的特征值见表5-8。
表5-8 轴向MFL检测信号的特征值定义
(2)径向分量 图5-53所示为示例弧面缺陷的径向MFL检测信号,该信号具有一个峰值点与一个谷值点,且沿轴向分别位于缺陷的左右开口处,因此将峰、谷值及对应点的轴向与周向间距选作特征值。同时,径向MFL检测信号的轮廓基本反映了缺陷的开口形状,有必要选取峰值区域和谷值区域的半径作为特征值。
此外,漏磁场径向分量的整体幅值反映了缺陷深度的相对大小,因此,选择径向MFL检测信号的体积和能量作为补充特征值。最终定义的径向MFL检测信号特征值见表5-9。
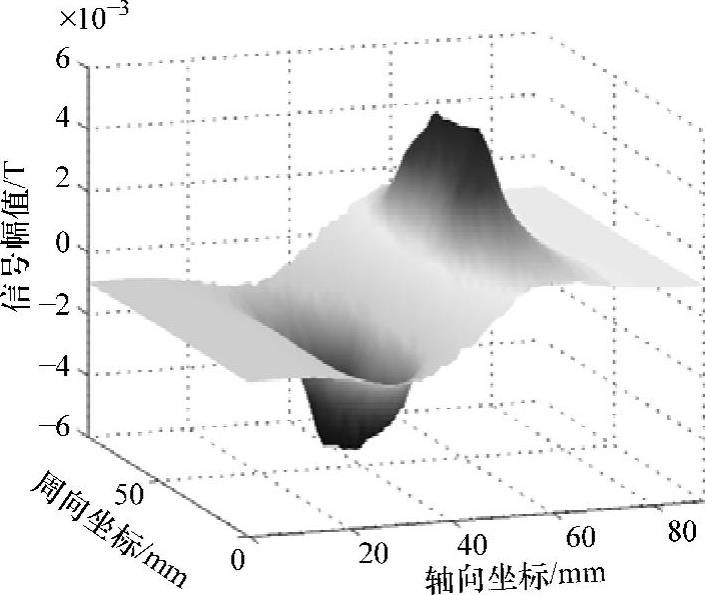
图5-53 28.6mm×7.2mm弧面缺陷的径向MFL检测信号
表5-9 径向MFL检测信号的特征值定义
(3)周向分量 图5-54所示为示例弧面缺陷的周向MFL检测信号。该信号具有两个峰值点与两个谷值点,且均位于缺陷开口边沿处,因此将峰、谷值及对应点的轴向与周向间距选作特征值。考虑到周向MFL检测信号的轮廓与缺陷侧面边界的一致性较好,有必要选取峰值区域和谷值区域的半径作为特征值。同时,周向MFL检测信号在缺陷开口边界处发生突变,因此将周向检测信号梯度最大值点的幅值与坐标选作特征值。
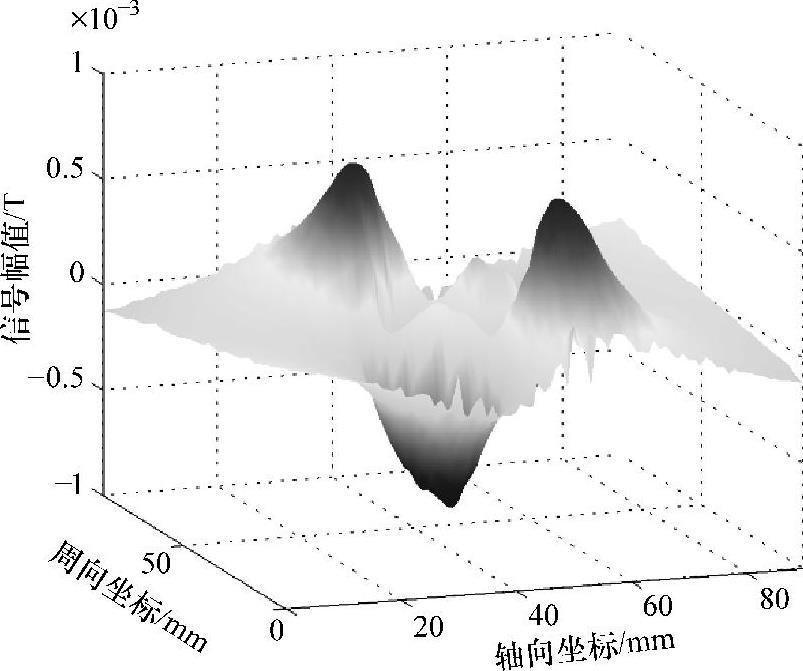
图5-54 28.6mm×7.2mm弧面缺陷的周向MFL检测信号
此外,漏磁场周向分量的整体幅值反映了缺陷深度的相对大小,故选择周向MFL检测信号的体积和能量作为补充特征值。最终定义的周向MFL检测信号特征值见表5-10。
表5-10 周向MFL检测信号的特征值定义

为了尽可能降低三维MFL检测信号中的数据冗余,应用主成分分析法对已经定义的三维MFL检测信号特征值进行分析,进而提取其中能有效反映缺陷轮廓参数的主要特征值。
主成分分析法是一种线性的数据降维方法,通过构建待处理数据空间的正交基,将含有数据冗余的多个变量以较少的几个变量进行简化表示,从而达到降低数据冗余和减小数据规模的目标。
前述已定义的三维MFL检测信号特征值包括15个轴向特征值、8个径向特征值和11个周向特征值。应用主成分分析法分析这34个特征值的基本步骤如下:
1)取x个试验缺陷D1,D2,…,Di,…,Dx-1,Dx,分别计算各个缺陷对应的34个三维MFL检测信号特征值P1,P2,…,P34。组合所有的特征值,得到用于分析的目标矩阵M,即
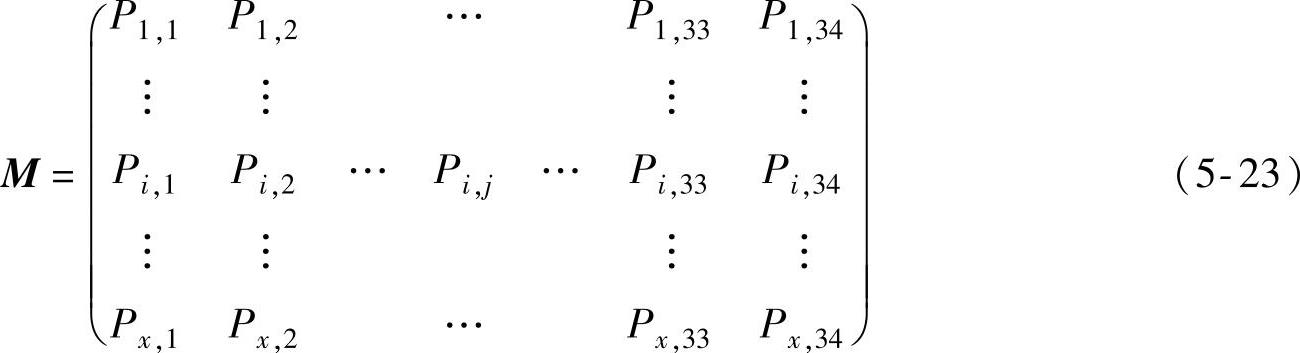
2)求出目标矩阵M的全部特征向量,计算每个特征向量V对应的成分占比,并按占比从高到低对所有特征向量进行排序。
3)设定用于判断三维MFL检测信号主要特征值的成分占比阈值δ。在上述的排序结果中,从前往后选取成分占比最大的k个特征向量V1,…,Vi,…,Vk。
4)选择特征向量V1,…,Vi,…,Vk在目标矩阵中所对应的三维MFL检测信号特征值P1,…,Pi,…,Pk,即为所求的三维MFL检测信号主要特征值。
首先基于一组弧面缺陷,提取三维MFL检测信号的主要特征值。其中,弧面缺陷直径的最小值、最大值及间隔分别为14.3mm、28.6mm和1.4mm,缺陷深度的最小值、最大值及间隔分别为1.4mm、7.2mm和1.4mm,缺陷总个数为55个。

图5-55 基于弧面缺陷的三维MFL检测信号特征值的主成分分析结果
分别求解各个缺陷三维MFL检测信号的34个特征值,并对这些特征值组成的矩阵进行主成分分析,得到图5-55所示的主成分分析结果。其中,为了显示方便,分析结果中仅列出了占比最大的前10个特征值。为了在减少数据冗余的同时保持尽可能高的准确度,设定特征值成分占比的阈值为90%,则所有的三维MFL检测信号特征值可用其中的7个主要特征值进行有效的表示。其中,所选定的7个主要特征值为Pa8、Pa9、Pa1、Pa2、Pr3、Pc4和Pa6。
为了对上述结果进行进一步的验证,分别基于矩形缺陷与圆柱缺陷提取三维MFL检测信号的主要特征值。两种缺陷的尺寸参数见表5-11,其中,矩形缺陷总个数为260个,圆柱缺陷总个数为55个。
表5-11 用于主要特征值提取的矩形缺陷与圆柱缺陷尺寸参数

图5-56和图5-57所示分别为基于矩形缺陷和圆柱缺陷所得到的三维MFL检测信号特征值主成分分析结果。其中,为了显示方便,分析结果中仅列出了占比最大的前10个特征值。设定特征值成分占比的阈值为90%,基于两个分析结果选定的7个主要特征值虽然先后顺序有所不同,但均为Pa8、Pa9、Pa1、Pa2、Pr3、Pc4和Pa6。
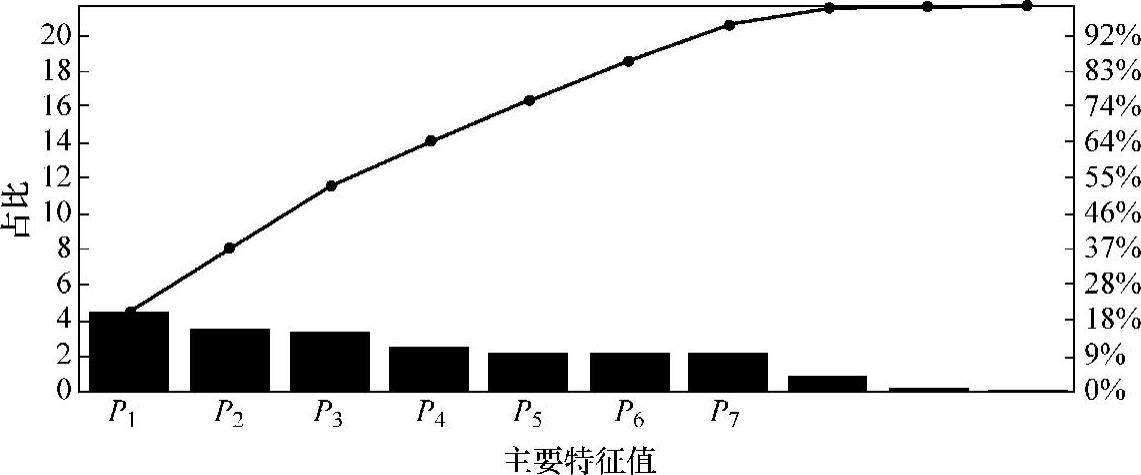
图5-56 基于矩形缺陷的三维MFL检测信号特征值的主成分分析结果
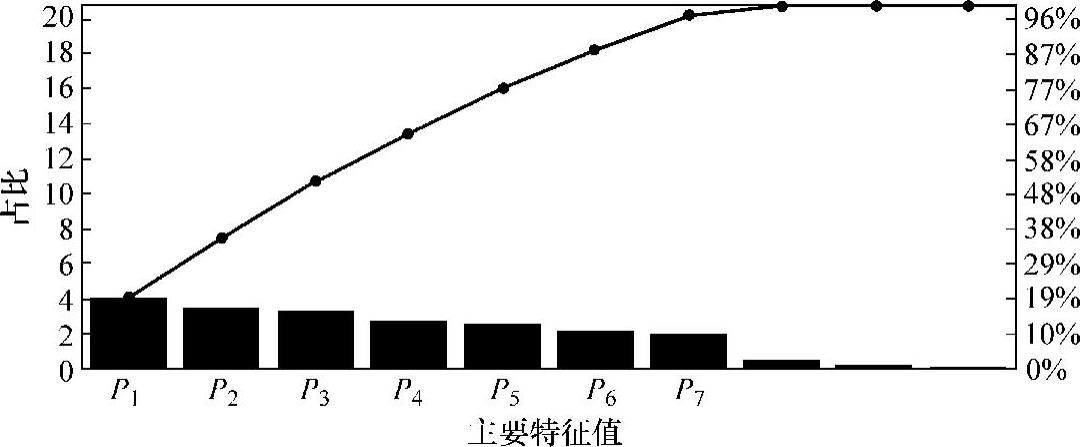
图5-57 基于圆柱缺陷的三维MFL检测信号特征值的主成分分析结果
由以上结果可知,在设定特征值成分占比的阈值为90%的前提下,无论是基于弧面缺陷、矩形缺陷或圆柱缺陷,应用主成分分析法提取的三维MFL检测信号主要特征值均为Pa8、Pa9、Pa1、Pa2、Pr3、Pc4和Pa6这7个特征值。因此,对于任意缺陷的三维MFL检测信号,均可通过这七个主要特征值进行有效的表示。
实际中,在对缺陷三维轮廓进行反演时,根据之前提出的缺陷开口轮廓检测方法,已由三维MFL检测信号的梯度信息检测出了缺陷的开口轮廓。主要特征值中Pa6对应的轴向MFL检测信号梯度最大值点坐标相当于已被求出,因而可以从主要特征值的列表中舍去,进而得到表5-12所列的用于缺陷轮廓反演的三维MFL检测信号主要特征值。
表5-12 用于缺陷轮廓反演的三维MFL检测信号主要特征值
在后续的缺陷三维轮廓反演过程中,将以主要特征值取代原始的三维MFL检测信号,作为人工神经网络的输入或输出。如此,可极大地减少人工神经网络中的神经元数量,从而降低网络的训练复杂度并减少训练时间。
2.缺陷三维轮廓条状模型
按之前提出的方法所检测出的缺陷开口轮廓,基本上划定了缺陷三维轮廓反演的待求解区域。在其基础上引入深度参数,即可建立缺陷三维轮廓人工神经网络反演所需要的缺陷三维模型。
为了尽可能减少缺陷三维模型的参数,提出由任意缺陷开口轮廓S建立缺陷三维轮廓条状模型的方法,具体步骤如下:
1)确定划分尺寸Δw,将管壁待求解区域沿周向划分为N等份。设缺陷开口轮廓外部的深度均为0,开口轮廓内部的每等份均为深度相同的等高平面,可得到如图5-58所示的初步划分结果。
2)求出缺陷开口轮廓内部任一等份的等价长度,将该等份用等价的长方形进行表示,如图5-59所示。其中,等价长方形的长度按下式进行计算,即
L=S/Δw (5-24)式中,S为该等份开口截面的面积;Δw为模型沿管道周向的划分尺寸。
3)组合各等份所对应的等价长方形,得到新的开口轮廓。确定各等份在管道径向方向的深度参数d,得到如图5-60所示的最终缺陷三维轮廓条状模型MS。
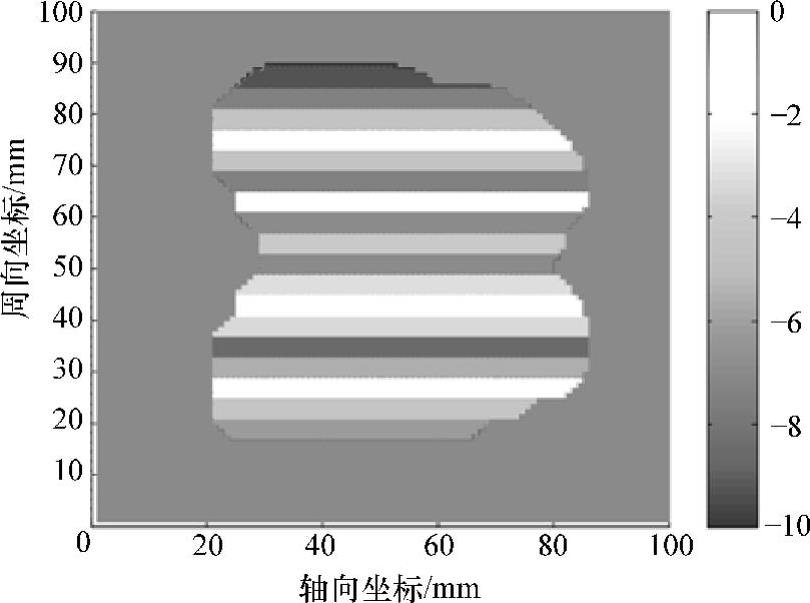
图5-58 缺陷开口轮廓的初步划分结果示例
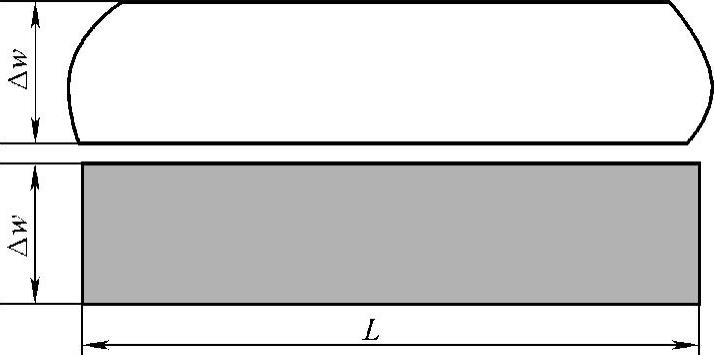
图5-59 缺陷开口轮廓任一等份的等价长方形表示
在该模型中,未知参数为各个等份的深度d。因此,令Li表示第i个等份的长度值,di表示第i个等份的深度值,则在已知沿管道周向划分尺寸Δw的前提下,可得到如下表示的缺陷三维轮廓条状模型,即
MS={(L1,d1),…,(Li,di),…,(LN,dN)} (5-25)
在该表达式中,缺陷开口轮廓内部的长度与深度参数为待求解的未知量。在缺陷开口轮廓外部,所有等份的长度与深度参数均为

图5-60 缺陷三维轮廓条状模型示例
Li=di=0 (5-26)
按所建立的条状模型,事实上为等高的条状近似模型,因而基于此模型的反演结果具有突变的非平滑边沿。考虑到与实际缺陷平滑边沿之间的差别,在实际的缺陷三维轮廓反演过程中,将对基于条状模型的反演结果进行适当的平滑处理,以得到较为平滑的缺陷边沿。
3.基于径向基函数人工神经网络的MFL检测信号正向预测
用于缺陷三维MFL检测信号正向预测的径向基函数(radial-basis function,RBF)人工神经网络的输入为基于三维轮廓条状模型的缺陷参数,输出为所提取的三维MFL检测信号主要特征值。在对正向预测人工神经网络进行训练时,将建立矩形、弧面和圆柱三类训练样本缺陷的等价条状模型。最后,基于训练后的RBF人工神经网络,进行缺陷MFL检测信号主要特征值的预测。
RBF人工神经网络满足缺陷三维轮廓量化的非线性映射要求,在隐含层单元数量足够的情况下,能以三层网络实现对任意连续函数的任意精度逼近,并且可保持其他前向型人工神经网络所不具备的最佳逼近性能。因此,可利用RBF人工神经网络进行缺陷三维MFL检测信号的正向预测。
图5-61所示为RBF人工神经网络的基本结构,包含输入层、输出层、隐含层三部分。设输入向量X含有M个分量,输出向量Y含有N个分量,则RBF人工神经网络输入与输出间的完整映射关系为
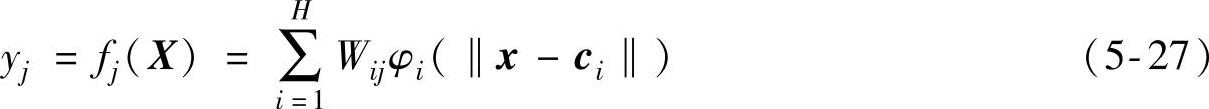
式中,yj为输出向量Y的第j个分量;φi为隐含层内的第i个基函数;ci为基函数φi的中心向量;Wij为隐含层第i个基函数与输出向量第j个分量之间的连接权值;H为隐含层内的神经元数量。
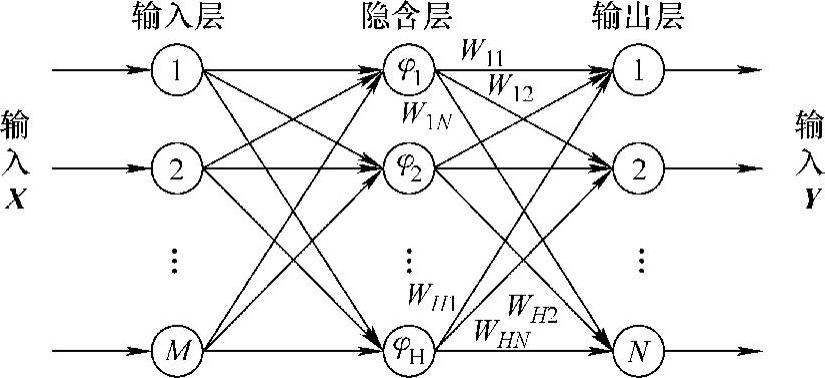
图5-61 RBF人工神经网络的结构
为了实现网络隐含层的非线性映射功能,选择如下的高斯函数作为RBF人工神经网络的基函数,即
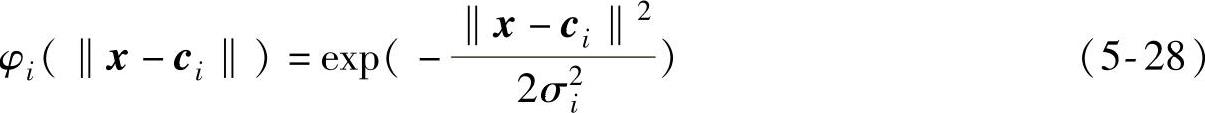
式中,ci和σi分别为高斯基函数的中心向量与宽度参数。
将高斯基函数的计算式代入人工神经网络,可得到RBF人工神经网络的完整的输入输出映射关系,即
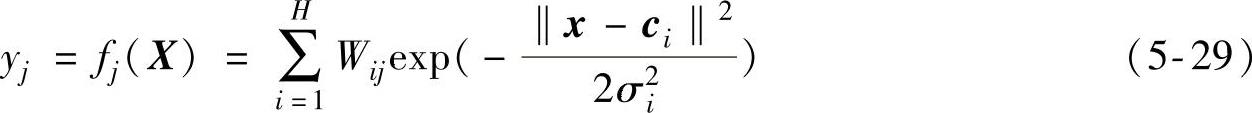
式中,ci和σi分别为高斯基函数的中心向量与宽度参数;Wij为隐含层第i个基函数与输出向量第j个分量之间的连接权值;H为隐含层内的神经元数量。
由图5-62所示的RBF人工神经网络迭代训练过程可知,通过调整网络连接权值与基函数参数,可不断减小网络实际输出与目标输出之间的差值。选择网络实际输出Y与目标输出T之间的均方误差作为网络训练过程中的目标函数,即
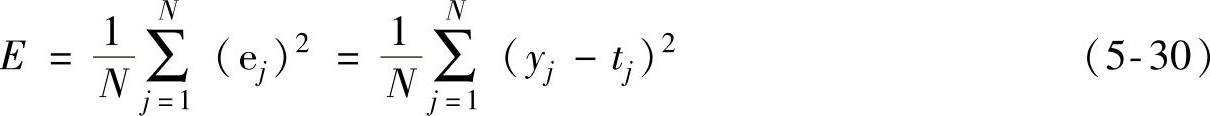
式中,yj和tj分别为网络实际输出Y与目标输出T的第j个分量;N为输出向量的分量个数。

图5-62 RBF人工神经网络迭代训练过程
在RBF人工神经网络的迭代训练过程中,采用梯度下降算法对网络隐含层与输出层之间的连接权值Wij进行迭代修正,可推导出如下的修正公式
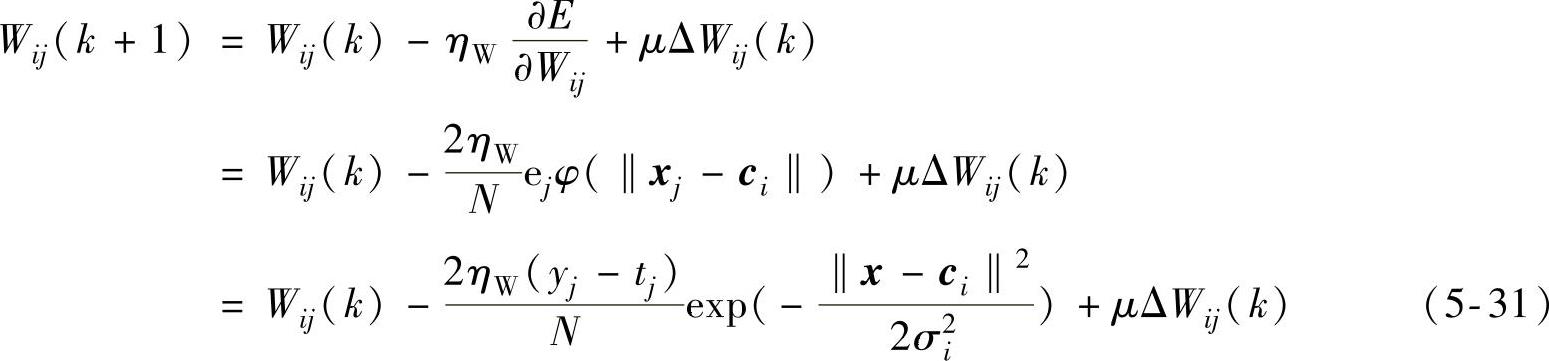
式中,ηW为算法的学习率,用于控制网络连接权值Wij修正算法的收敛速度。
高斯基函数的中心向量ci与宽度σi也采用梯度下降法进行修正,可推导出如下的迭代修正公式
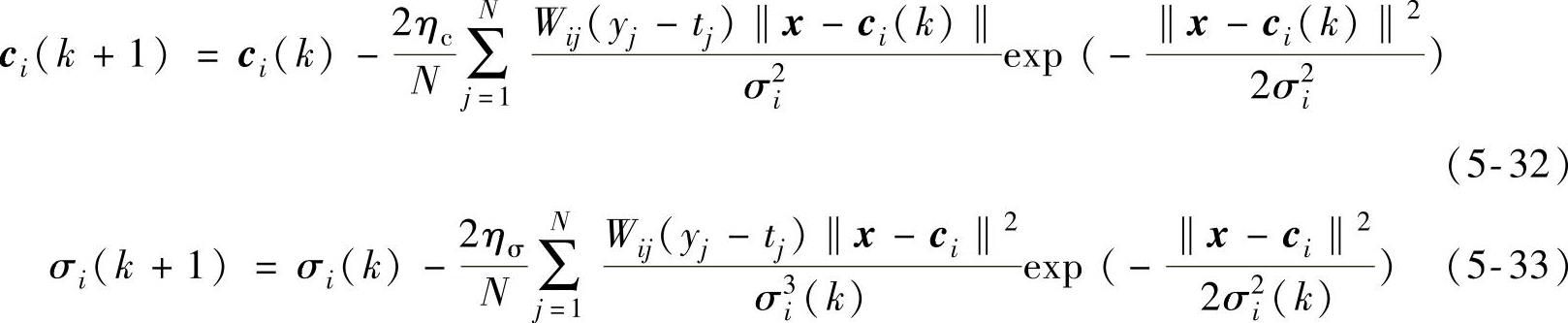
式中,ηc和ησ分别用于控制中心向量ci与宽度σi修正算法的收敛速度。
基于提取的三维MFL检测信号主要特征值和建立的缺陷三维轮廓条状模型,使用RBF人工神经网络进行MFL检测信号的正向预测。其中,将缺陷三维轮廓条状模型中的参数作为RBF人工神经网络的输入,即
MS={(L1,d1),…,(Li,di),…,(LN,dN)} (5-34)
式中,Li和di分别表示缺陷三维轮廓条状模型中第i个等份的长度值与深度值。
正向预测RBF人工神经网络的输出,则为提取的6个能有效反映缺陷轮廓参数的缺陷三维MFL检测信号主要特征值。
图5-63所示为正向预测RBF人工神经网络迭代训练过程。对于任意缺陷,依据缺陷三维轮廓条状模型,可得到该缺陷对应的条状模型参数表示MS。将MS代入RBF人工神经网络,得到预测的MFL检测信号6个主要特征值组成的向量PP。进而计算预测结果PP与实际缺陷三维MFL检测信号主要特征值向量PR之间的均方误差E,即
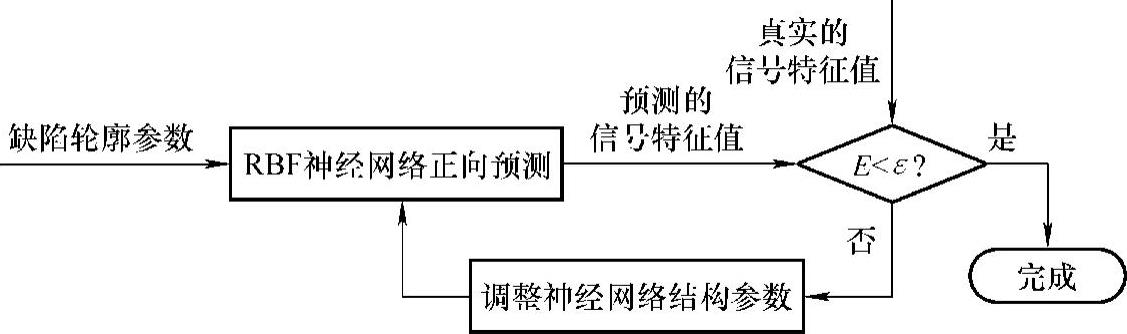
图5-63 正向预测RBF人工神经网络迭代训练过程

式中,PPj和PRj分别为网络预测及实际的第j个MFL检测信号主要特征值。(https://www.xing528.com)
将上述误差公式代入梯度下降算法,进而推导出如下的网络连接权值Wij、基函数中心向量ci及宽度σi的迭代修正公式为
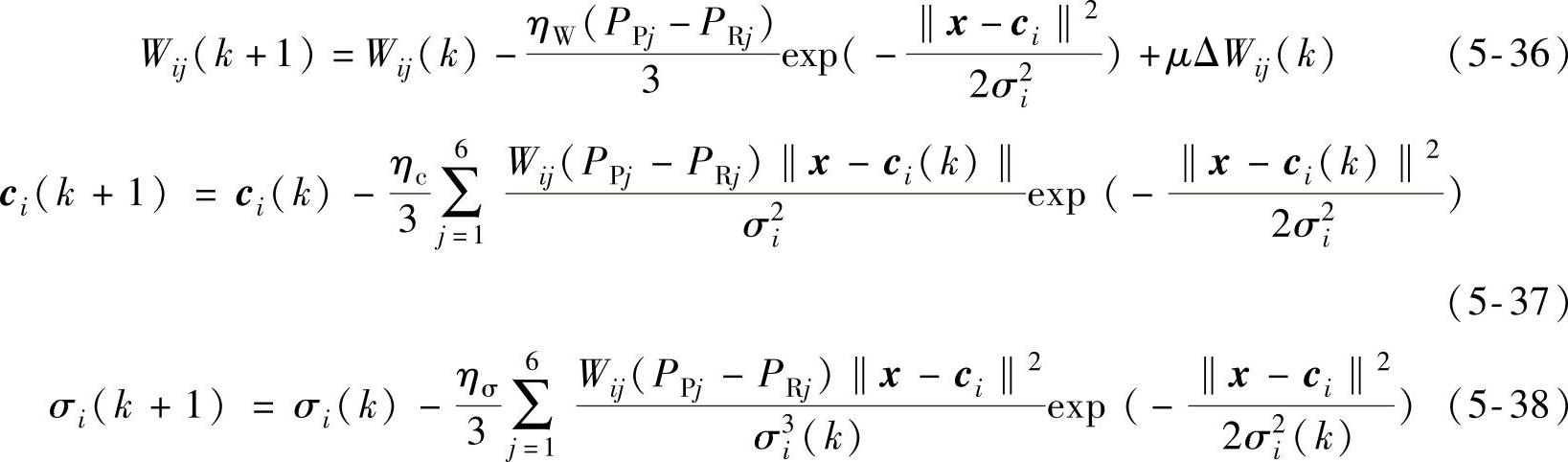
式中,ηW、ηc和ησ分别用于控制网络连接权值Wij、基函数中心向量ci及宽度σi修正算法的收敛速度。
为了训练RBF人工神经网络,建立了基于样本缺陷的三维MFL检测信号数据库。其中,用于建立数据库的样本缺陷,包括矩形缺陷、弧面缺陷和圆柱缺陷三类。然而,这三类样本缺陷的实际轮廓并不完全符合之前所提出的三维轮廓条状模型。因此,将分别建立与其实际轮廓相对应的等价条状模型。
(1)矩形缺陷的等价模型 在确定了划分尺寸Δw的情况下,只需将矩形缺陷沿管道周向进行划分,即可快速建立其等价的缺陷三维轮廓条状模型。
若按划分尺寸Δw可正好将缺陷划分为N等份,则每等份的底部均为等高平面,且其开口均为长度和宽度分别为L和Δw的长方形,因此无需进行额外的等价处理和计算。直接组合各个等份,即可得到矩形缺陷的等价三维轮廓条状模型MSR。在划分尺寸为Δw的情况下,基于该等价条状模型,可将L×W×H的矩形缺陷表示为
MSR={(L1,H1),…,(Li,Hi),…,(Lk,Hk)} (5-39)
式中,每个等份的长度均为Li=L,其深度均为Hi=H。
若按划分尺寸Δw并未正好将缺陷划分为N等份,则缺陷内部的等份无需进行额外的处理,但是缺陷边沿处的等份需要进行等价处理。在缺陷边沿处,划分得到的长方体的长度和深度仍分别为L和H,设其宽度为WX。将该长方体用长度和宽度分别为L和Δw的等价长方体代替,其等价深度为
HX=HWX/Δw (5-40)
最终得到的矩形缺陷等价三维轮廓条状模型MSR如图5-64所示。

图5-64 矩形缺陷等价三维轮廓条状模型示意图
a)真实缺陷 b)等价模型
(2)圆柱缺陷的等价模型 在确定了划分尺寸Δw的情况下,将圆柱缺陷沿管道周向进行划分,然后按照下述步骤建立等价的缺陷三维轮廓条状模型。
无论按划分尺寸Δw能否正好将缺陷划分为N等份,所有的划分等份均需要进行等价处理。令圆柱缺陷的深度为H,设任意划分的面积为SX,将该划分用宽度和深度分别为Δw和H的等价长方体代替,可得到长方体的长度为
LX=SX/Δw (5-41)
组合各个等份,即可得到如图5-65所示的圆柱缺陷等价三维轮廓条状模型MSC。在划分尺寸为Δw的情况下,基于该等价条状模型,可将D×H的圆柱缺陷表示为
MSC={(L1,H1),…,(Li,Hi),…,(Lk,Hk)} (5-42)
式中,每个等份的深度均为Hi=H;长度Li按式(5-41)进行计算。

图5-65 圆柱缺陷等价三维轮廓条状模型示意图
a)真实缺陷 b)等价模型
(3)弧面缺陷的等价模型 在确定了划分尺寸Δw的情况下,将弧面缺陷沿管道周向进行划分,然后按照下述步骤建立其等价的缺陷三维轮廓条状模型。
无论按划分尺寸Δw能否正好将缺陷划分为N等份,所有的划分等份均需要进行等价处理。设任意划分的面积和体积分别为SX和VX,将该划分用宽度为Δw的等价长方体代替,可得到长方体的长度LX和深度HX分别为
LX=SX/Δw (5-43)
HX=VX/SX (5-44)
组合各个等份,即可得到如图5-66所示的弧面缺陷等价三维轮廓条状模型MSA。在划分尺寸为Δw的情况下,基于该等价条状模型,可将D×H的弧面缺陷表示为
MSA={(L1,H1),…,(Li,Hi),…,(Lk,Hk)} (5-45)
式中,每个等份的长度Li和深度Hi分别按式(5-43)和式(5-44)进行计算。

图5-66 弧面缺陷等价三维轮廓条状模型示意图
a)真实缺陷 b)等价模型
为了训练正向预测RBF人工神经网络,建立基于口径为457mm、壁厚为14.3mm管道的样本缺陷数据库。表5-13列出了全部缺陷样本的详细尺寸参数。其中,样本数据库中的缺陷类型包括矩形缺陷、弧面缺陷和圆柱缺陷三类,对应的缺陷个数分别为260、55和55。
表5-13 人工神经网络训练样本缺陷的尺寸参数

在所建立的缺陷样本数据中,随机选择70%和15%的缺陷样本用于人工神经网络的训练与验证。缺陷样本库中剩余的15%缺陷样本,用于对训练得到的RBF人工神经网络进行测试分析。
采用梯度下降算法,对正向预测RBF人工神经网络进行训练,得到如图5-67所示的训练过程误差收敛曲线。由该曲线可知,在正向预测RBF人工神经网络的训练过程中,基于梯度下降算法的迭代修正方法使得网络的预测输出以较快的速度逼近目标输出。经过5000次左右的训练,网络收敛到期望的误差值,达到了根据缺陷三维轮廓条状模型参数预测MFL检测信号主要特征值的精度要求。
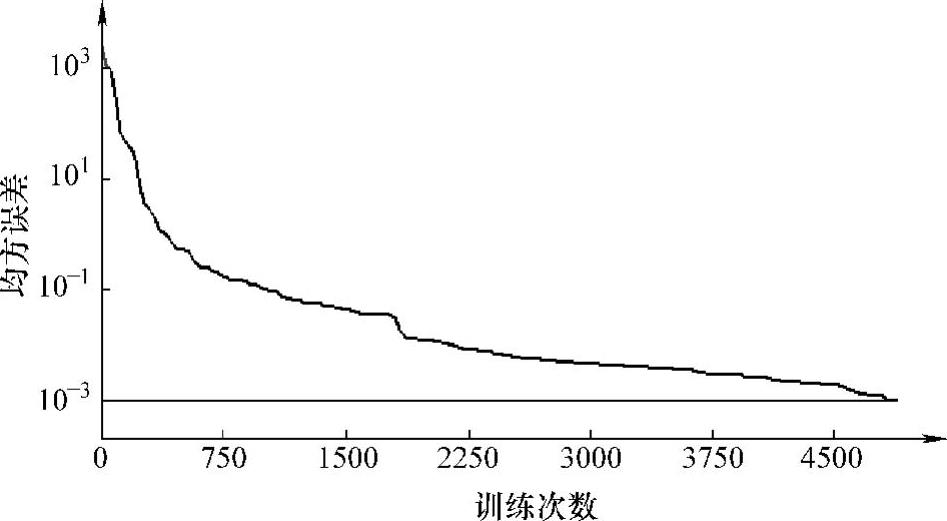
图5-67 正向预测RBF人工神经网络训练过程的误差收敛曲线
在实际应用过程中,若训练后的RBF人工神经网络仍不能满足预测精度的要求,可通过修改神经元个数、改变网络训练算法、增加试验数据等方法对人工神经网络进行调整,进而重新训练直至达到预定的预测精度。在得到满足要求的RBF人工神经网络后,即可基于任意的缺陷三维轮廓条状模型参数,预测对应的三维MFL检测信号主要特征值。
基于训练得到的正向预测RBF人工神经网络,利用非样本库中的缺陷进行MFL检测信号正向预测试验,以验证所建立的RBF人工神经网络的预测精度、灵敏度和对实际不规则缺陷的适用性。
利用不在样本库中的矩形缺陷、弧面缺陷和圆柱缺陷进行正向预测试验,以验证正向预测RBF人工神经网络的预测精度。在建立每个试验缺陷的三维轮廓等价条状模型的基础上,通过正向预测RBF人工神经网络预测缺陷三维MFL检测信号的主要特征值,进而计算预测结果与实际MFL检测信号主要特征值之间的误差。
为了验证RBF人工神经网络对MFL检测信号主要特征值的预测精度,定义如下的主要特征值预测误差,即
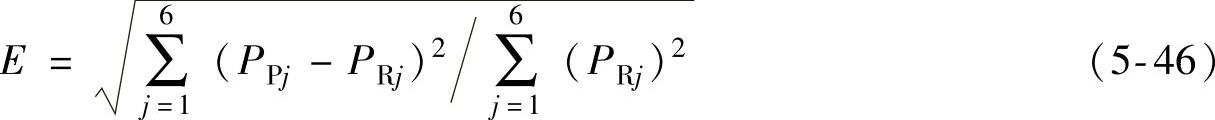
式中,PPj和PRj分别为网络预测及实际的MFL检测信号主要特征值。
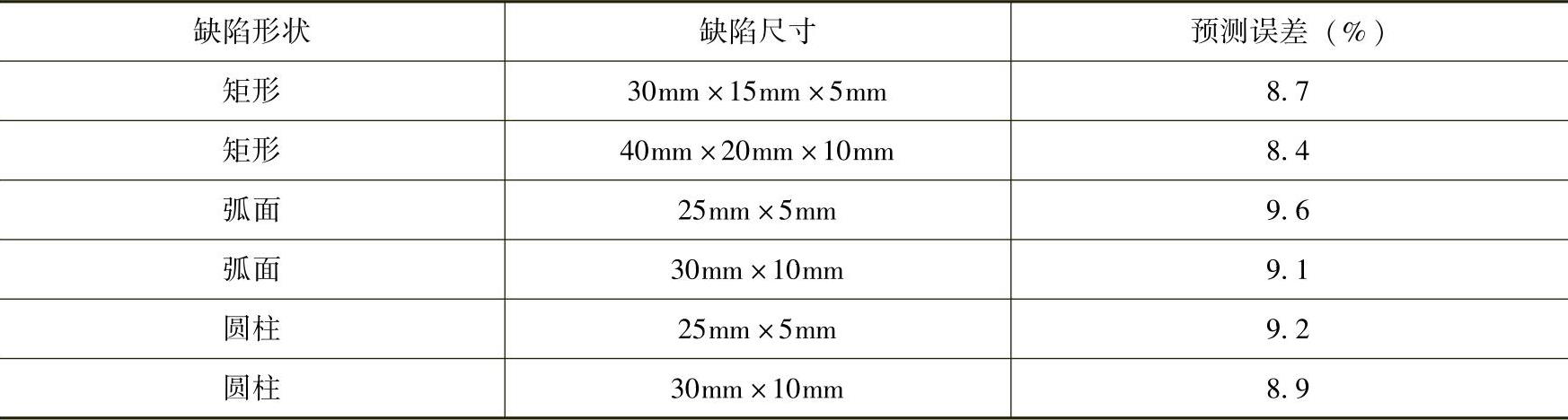
统计试验缺陷三维MFL检测信号主要特征值的预测误差见表5-14。由统计结果可知,基于所建立的正向预测RBF人工神经网络,试验缺陷三维MFL检测信号主要特征值的预测误差均不超过10%。这表明所建立的RBF人工神经网络具有较高的预测精度。
表5-14 缺陷三维MFL检测信号主要特征值的预测误差
为了验证正向预测RBF人工神经网络在缺陷轮廓参数改变时的灵敏度,在缺陷三维轮廓条状模型的参数中添加1%、2%及5%的随机噪声干扰,再进行缺陷MFL检测信号主要特征值的预测试验。统计不同噪声水平下缺陷三维MFL检测信号主要特征值的预测误差见表5-15。
表5-15 不同噪声水平下缺陷三维MFL检测信号主要特征值的预测误差
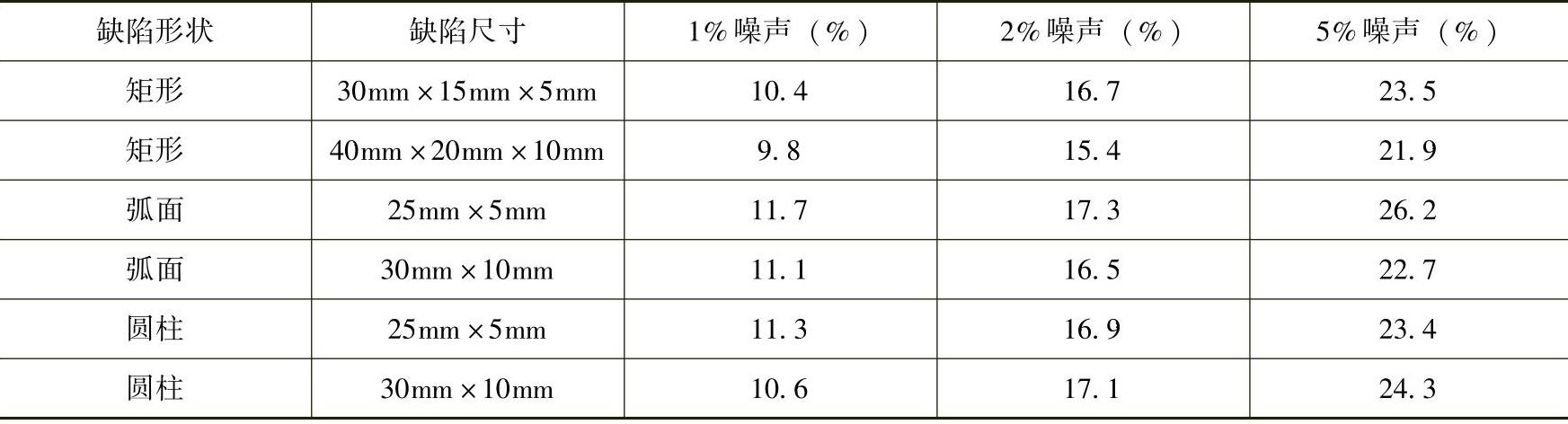
由上述误差统计结果可知,与无噪声情况下的预测结果相比,当在缺陷条状模型参数中添加噪声干扰后,三维MFL检测信号主要特征值的预测误差随噪声水平的提高而显著增大。这表明所建立的正向预测RBF人工神经网络对缺陷条状模型参数具有较高的灵敏度,在缺陷模型参数改变时可以对预测的MFL检测信号主要特征值做出迅速修正。
为了进一步验证所建立的正向预测RBF人工神经网络对于实际管道中不规则缺陷的适用性,对图5-68所示的不规则缺陷的MFL检测信号主要特征值进行预测,进而计算预测结果与实际的MFL检测信号主要特征值之间的误差。
经计算,RBF人工神经网络预测结果与真实MFL检测信号特征值之间的误差为14.1%。该误差虽然大于对规则缺陷的预测误差,但仍在可接受的范围内,证实了所建立的RBF人工神经网络作为正向模型对实际管道中不规则缺陷进行预测的可行性。因此,所建立的正向预测RBF人工神经网络,可用于对任意形状缺陷MFL检测信号主要特征值的预测。
4.缺陷三维轮廓的RBF人工神经网络迭代反演
由于缺陷三维轮廓反演属于病态的MFL检测逆问题,加之训练使用缺陷样本的类型仅包括矩形、弧面与圆柱三种,人工神经网络直接反演方法存在反演精度低和泛化能力不足的问题,不能直接用于缺陷三维轮廓的反演。
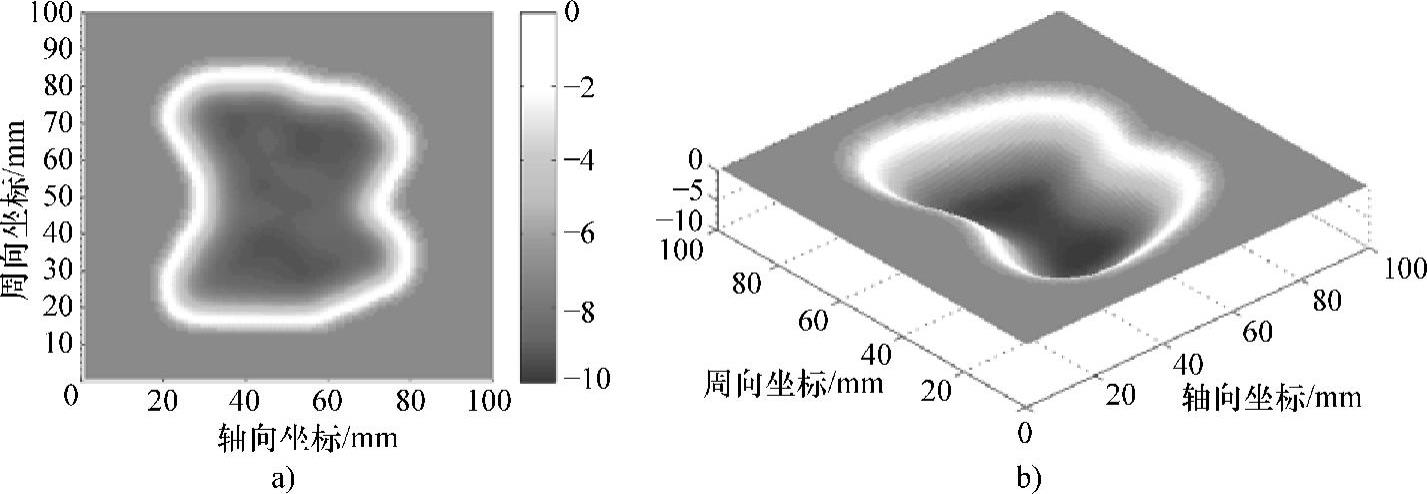
图5-68 用于MFL检测信号主要特征值正向预测试验的不规则缺陷
a)平面显示 b)立体显示
考虑到迭代法具有较高的反演精度和较强的泛化适用能力,提出缺陷三维轮廓的人工神经网络迭代反演方法。所提出的反演方法的基本思路为:首先训练得到MFL检测信号正向预测人工神经网络,进而将其作为正向求解模型嵌入迭代循环,以迭代修正的方法对缺陷的三维轮廓进行反演。
如此,人工神经网络用于求解良态的MFL检测信号正向问题而非病态的MFL检测信号逆问题,因此可以获得较高的预测精度。而在反演速度方面,可快速进行预测的人工神经网络替代了迭代法中原有的有限元计算,可使迭代过程中求解MFL检测信号正向问题的速度大幅提高。此外,人工神经网络的输入输出数据之间的映射关系明确,可方便进行微分求解计算,因此可以应用梯度下降法等确定性算法,对缺陷轮廓参数进行快速的迭代修正,从而获得更快的缺陷三维轮廓反演速度。
图5-69所示为嵌入正向预测RBF人工神经网络的缺陷三维轮廓迭代反演方法的基本流程。其中,正向预测RBF人工神经网络用于由缺陷轮廓到MFL检测信号的正向预测,其输入数据为基于三维轮廓条状模型的缺陷参数,输出数据为能有效反映缺陷轮廓参数的三维MFL检测信号主要特征值。
由图5-69可以得到由三维MFL检测信号进行缺陷三维轮廓人工神经网络迭代反演的基本步骤:
1)检测出缺陷开口轮廓S,并提取缺陷三维MFL检测信号的主要特征值,组成相应的主要特征值向量PR。
2)设定划分宽度W,基于开口轮廓检测结果S建立缺陷三维轮廓条状模型MS,其中各个划分的长度向量L为已知量,而深度向量H为待求量。
3)设定初始的缺陷深度向量H。
4)基于RBF人工神经网络进行正向预测,得到预测的主要特征值向量PP。
5)计算PP与PR之间的误差E,若E小于阈值δ,则结束迭代反演,获得经过平滑处理的最终缺陷轮廓;否则,对缺陷深度向量H进行修正,并跳转至步骤4),继续进行迭代反演。
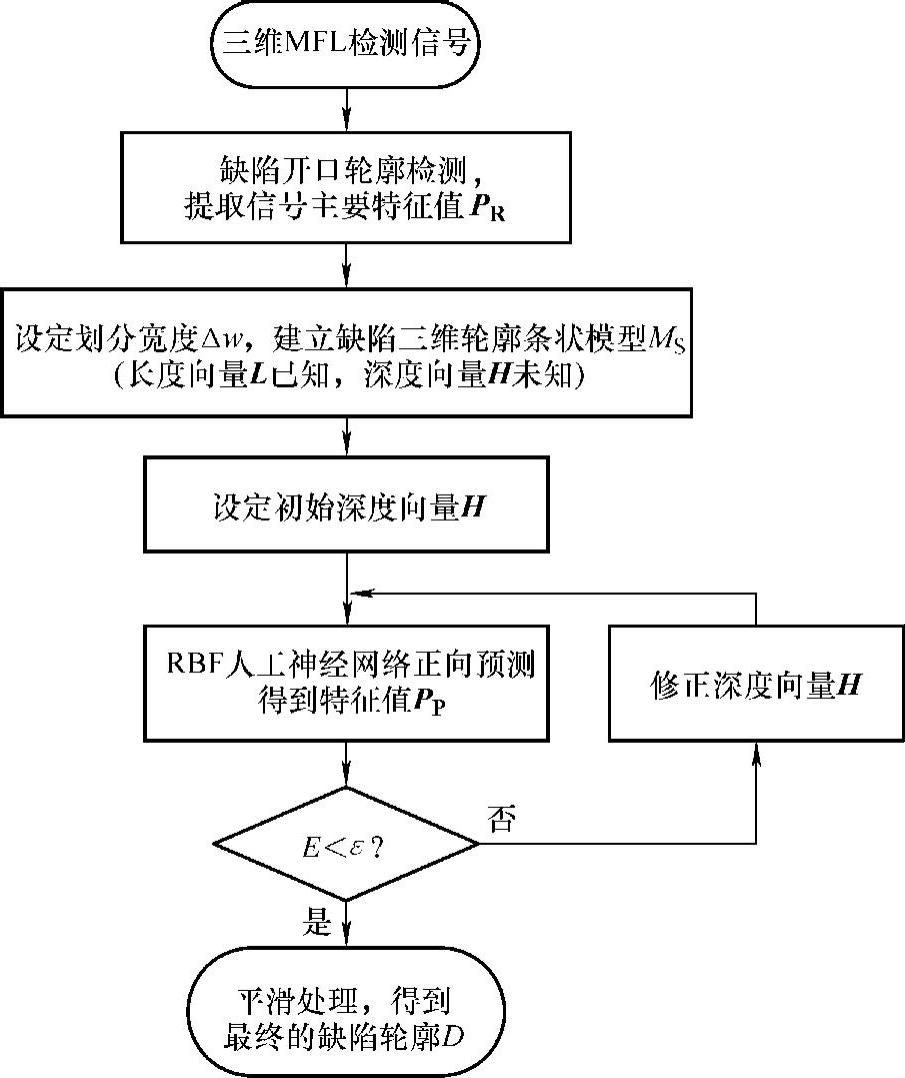
图5-69 缺陷三维轮廓RBF人工神经网络迭代反演方法的基本流程
在基于样本缺陷进行训练后,建立的正向预测RBF人工神经网络中的连接权值Wij、高斯基函数的中心向量ci及宽度σi均为已知值。因此,由正向预测RBF人工神经网络输入输出数据之间的映射关系,得到确定的关系表达式为
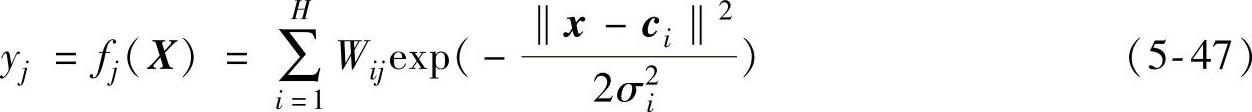
式中,X为输入的基于三维轮廓条状模型的缺陷参数向量;yj为输出向量Y的第j个分量,表示MFL检测信号的第j个主要特征值。
为了对缺陷参数向量进行迭代修正,将MFL检测信号主要特征值向量的预测结果PP与实际值PR之间的误差E定义为

式中,PPj和PRj分别为预测MFL检测信号与实际MFL检测信号的第j个主要特征值。
由式(5-47)和式(5-48)求出误差E对任意缺陷参数xi的一阶导数
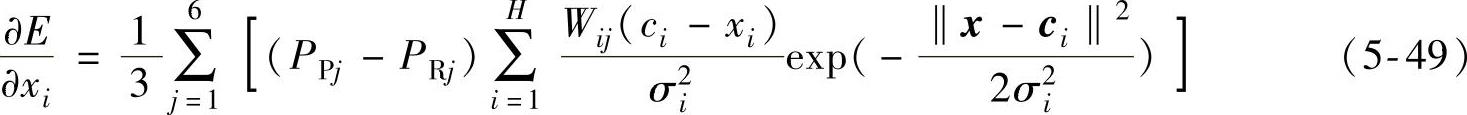
在缺陷三维轮廓的迭代反演过程中,基于重力下降算法,利用上述一阶导数对缺陷参数X进行迭代修正,可推导出如下的修正公式,即
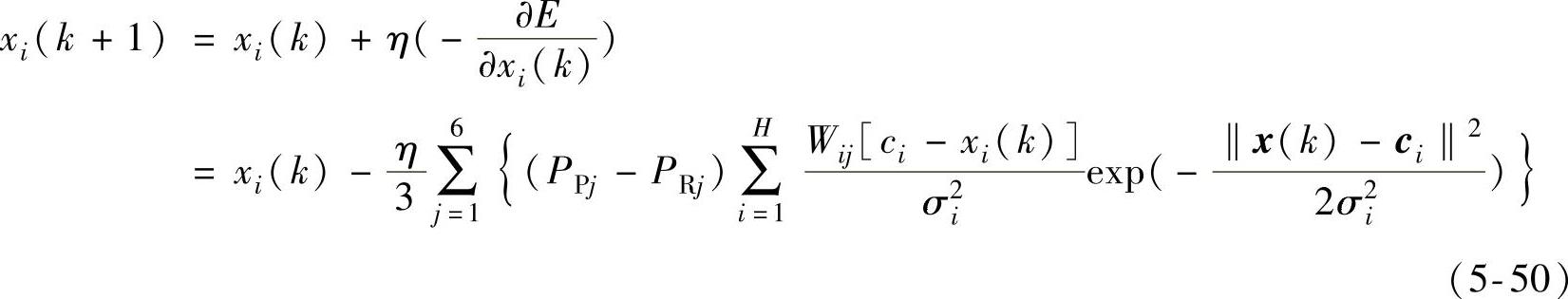
若单纯使用重力下降算法,迭代反演过程可能陷入局部最优点,从而不能收敛到全局最优的缺陷参数向量。为此,定义虚拟的温度变量T,引入模拟退火条件以扩大算法的搜索空间。在每次迭代过程中,当缺陷参数向量由Xk向Xk+1进行更新时,新的缺陷参数Xk+1仅在下式成立时才被接受,即

式中,Ek和Ek+1分别为对应于缺陷参数Xk和Xk+1的预测结果误差。
由式(5-51)可知,当Ek>Ek+1时,新的缺陷轮廓参数比现有参数更优,Xk一定更新为Xk+1;而当Ek<Ek+1时,新的缺陷轮廓参数相比于现有参数并未改进,Xk以一定的概率更新为Xk+1。如此,迭代反演过程可以摆脱局部最优解,从而继续搜索全局最优的缺陷轮廓参数。
为加快迭代反演过程的全局收敛速度,每当迭代过程进行一定次数时,可视为已在当前的温度参数T下处于平衡状态,按下式对温度参数T进行修正
Tk+1=αTk,0<α<1 (5-52)
式中,α的取值通常为0.8~0.95。
人工神经网络迭代反演方法的终止判据有以下三种:误差E小于一定的阈值δE;温度参数T小于一定的阈值δT;连续k次搜索,得到的缺陷轮廓对应的误差未发生改变。当以上任一判别条件成立时,迭代反演过程终止。此时,由缺陷参数得到基于条状模型的缺陷轮廓,进而对其进行适当的平滑处理,以得到较为平滑的边沿。
通过缺陷三维轮廓反演试验,对RBF人工神经网络迭代反演方法的精度、抗干扰能力及对未知形状缺陷的泛化能力进行研究。
基于RBF人工神经网络迭代反演方法,分别反演30mm×20mm×5mm矩形缺陷、30mm×5mm弧面缺陷和30mm×5mm圆柱缺陷的三维轮廓,结果如图5-70~图5-72所示。由图可知,由于在条状模型的最外边沿处进行了等价处理,试验缺陷反演结果的开口形状存在稍大的误差。但是在极值点的位置与深度等方面,反演轮廓与真实轮廓仍具有较好的一致性。
表5-16所列为试验缺陷三维轮廓反演误差的统计结果。由表可知,试验所用矩形、弧面及圆柱缺陷三维轮廓反演结果的均方根误差分别为15.7%、12.4%和13.2%。相比于随机搜索迭代反演方法,人工神经网络迭代反演方法的反演误差稍大,但其反演过程所消耗的时间几乎可以不计,具有前者所不具备的快速性。
表5-16 缺陷三维轮廓的反演误差

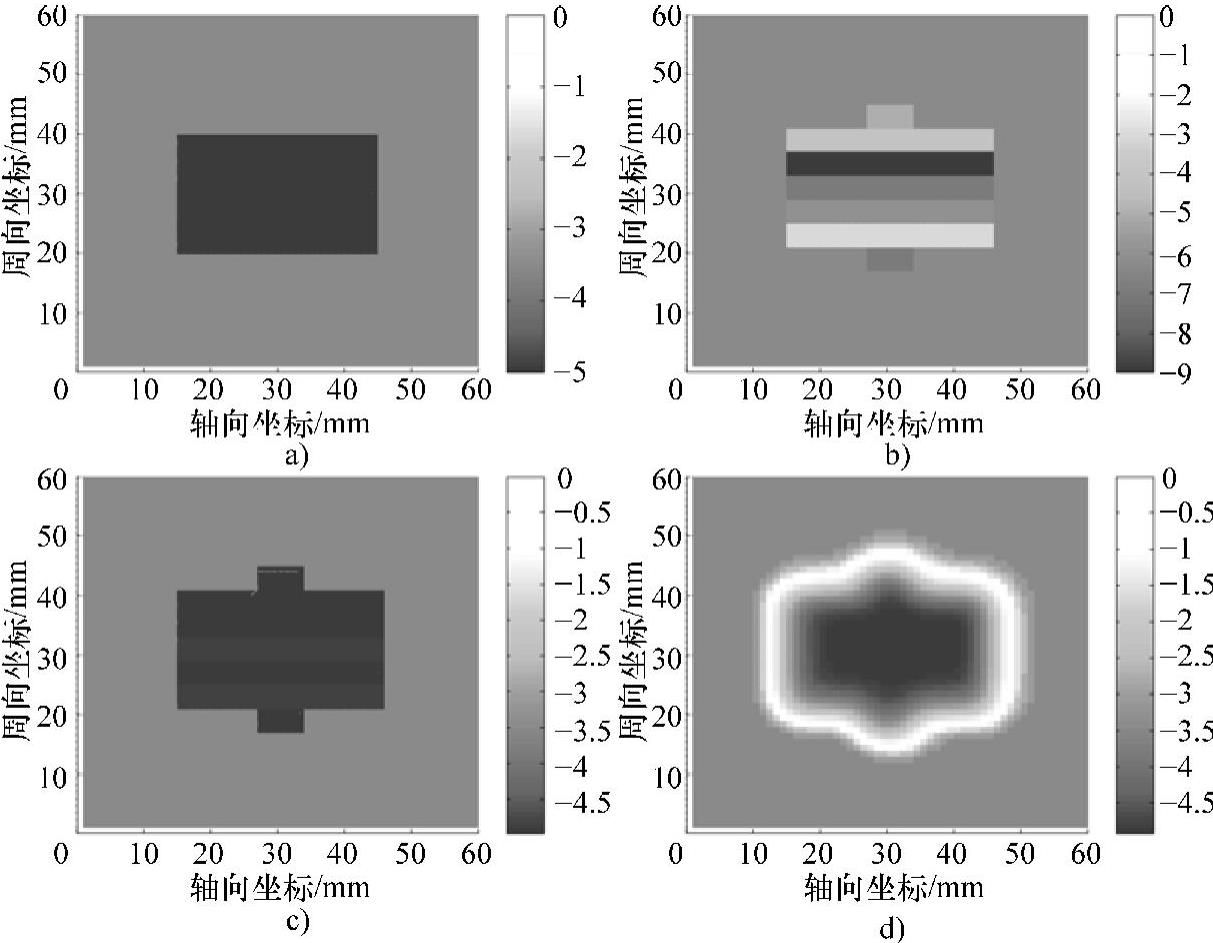
图5-70 30mm×20mm×5mm矩形缺陷轮廓的RBF人工神经网络迭代反演
a)真实轮廓 b)由开口轮廓识别结果建立的条状模型 c)条状模型的反演结果 d)最终的缺陷轮廓
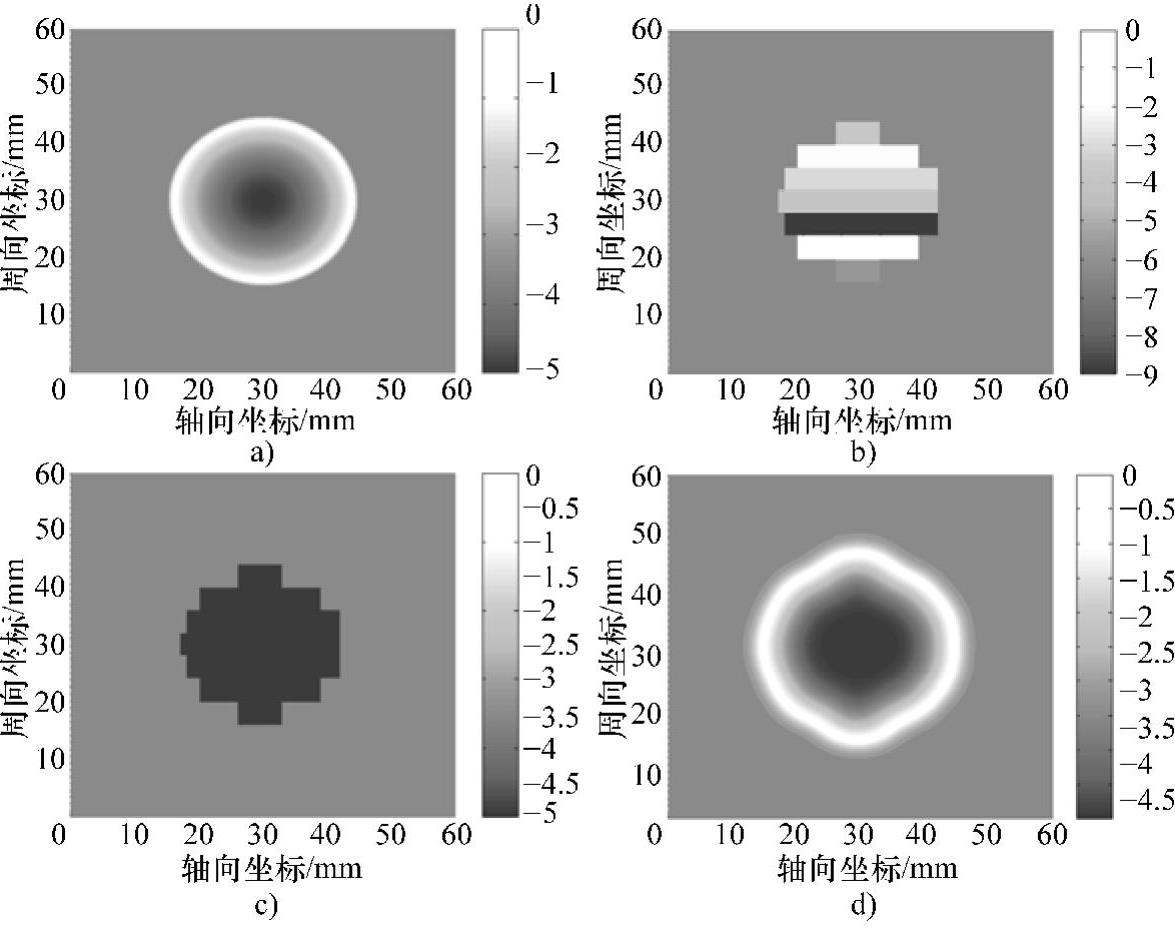
图5-71 30mm×5mm弧面缺陷轮廓的RBF人工神经网络迭代反演
a)真实轮廓 b)由开口轮廓识别结果建立的条状模型 c)条状模型的反演结果 d)最终的缺陷轮廓
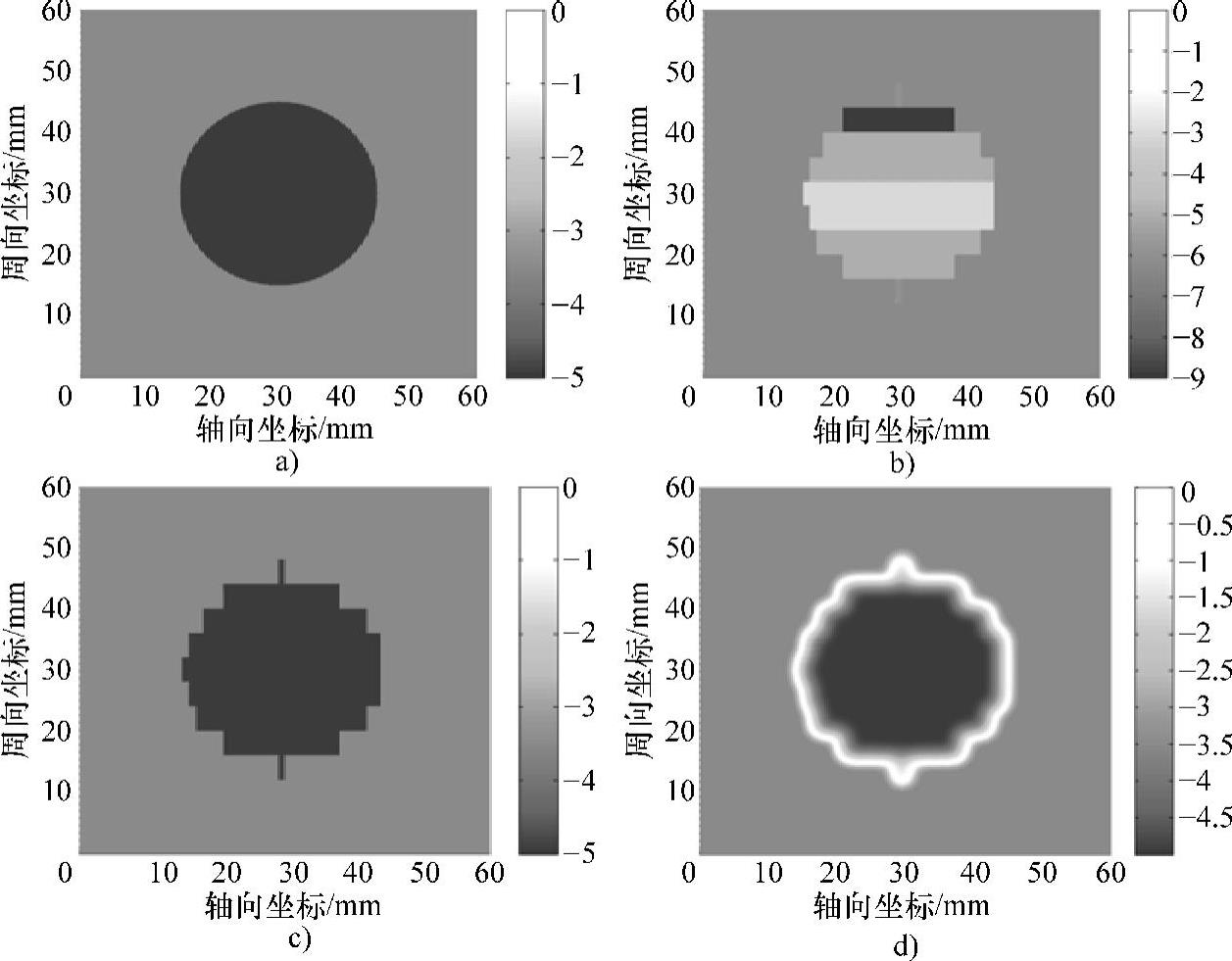
图5-72 30mm×5mm圆柱缺陷轮廓的RBF人工神经网络迭代反演
a)真实轮廓 b)由开口轮廓识别结果建立的条状模型 c)条状模型的反演结果 d)最终的缺陷轮廓
在试验缺陷的三维MFL检测信号中添加1%、2%和5%的随机噪声,进而用RBF人工神经网络迭代反演方法重新进行缺陷三维轮廓反演试验,得到如图5-73、图5-74和图5-75所示的反演结果。通过直接观察可知,随着噪声水平的提高,反演轮廓与真实轮廓间的差别也呈现逐渐增大的趋势。

图5-73 不同噪声下30mm×20mm×5mm矩形缺陷轮廓的RBF人工神经网络迭代反演结果
a)1%噪声 b)2%噪声 c)5%噪声
表5-17统计了各个试验缺陷在不同噪声水平下的反演误差。与表5-16对比可知,当在三维MFL检测信号中添加噪声干扰后,基于RBF人工神经网络迭代反演方法的缺陷三维轮廓反演误差显著增大。以30mm×20mm×5mm矩形缺陷为例,在1%的噪声水平下,该缺陷反演结果的均方根误差为16.4%;而在5%的噪声水平下,该缺陷反演结果的均方根误差达到了28.5%。

图5-74 不同噪声下30mm×5mm弧面缺陷轮廓的RBF人工神经网络迭代反演结果
a)1%噪声 b)2%噪声 c)5%噪声

图5-75 不同噪声下30mm×5mm圆柱缺陷轮廓的RBF人工神经网络迭代反演结果
a)1%噪声 b)2%噪声 c)5%噪声
表5-17 不同噪声水平下的缺陷三维轮廓反演误差

相比于随机搜索迭代反演方法的反演结果,人工神经网络迭代反演方法的反演误差更大,其反演误差随噪声水平提高的增幅也更大。这表明人工神经网络迭代反演方法的反演结果受噪声的影响更大,该方法的抗干扰能力相对较弱。
实际油气管道中缺陷的形状,与用于人工神经网络训练的矩形、弧面、圆柱等样本缺陷的形状差别很大。为此,基于图5-76所示的不规则缺陷,研究人工神经网络迭代反演方法对于未知形状缺陷的泛化能力。
由图5-76所示反演结果可知,试验缺陷的开口轮廓识别结果与真实开口轮廓基本一致,其最终反演轮廓与真实缺陷轮廓也比较相似。经计算,该不规则缺陷三维轮廓反演结果的均方根误差为21.4%。考虑人工神经网络迭代反演方法的快速性,该误差仍在可接受的范围内。然而,与随机搜索迭代反演方法相比,在相同的缺陷开口轮廓识别结果下,人工神经网络迭代反演方法的反演误差相对增大了72.6%。这表明人工神经网络迭代反演方法对实际管道中不规则缺陷的泛化能力相对要弱。
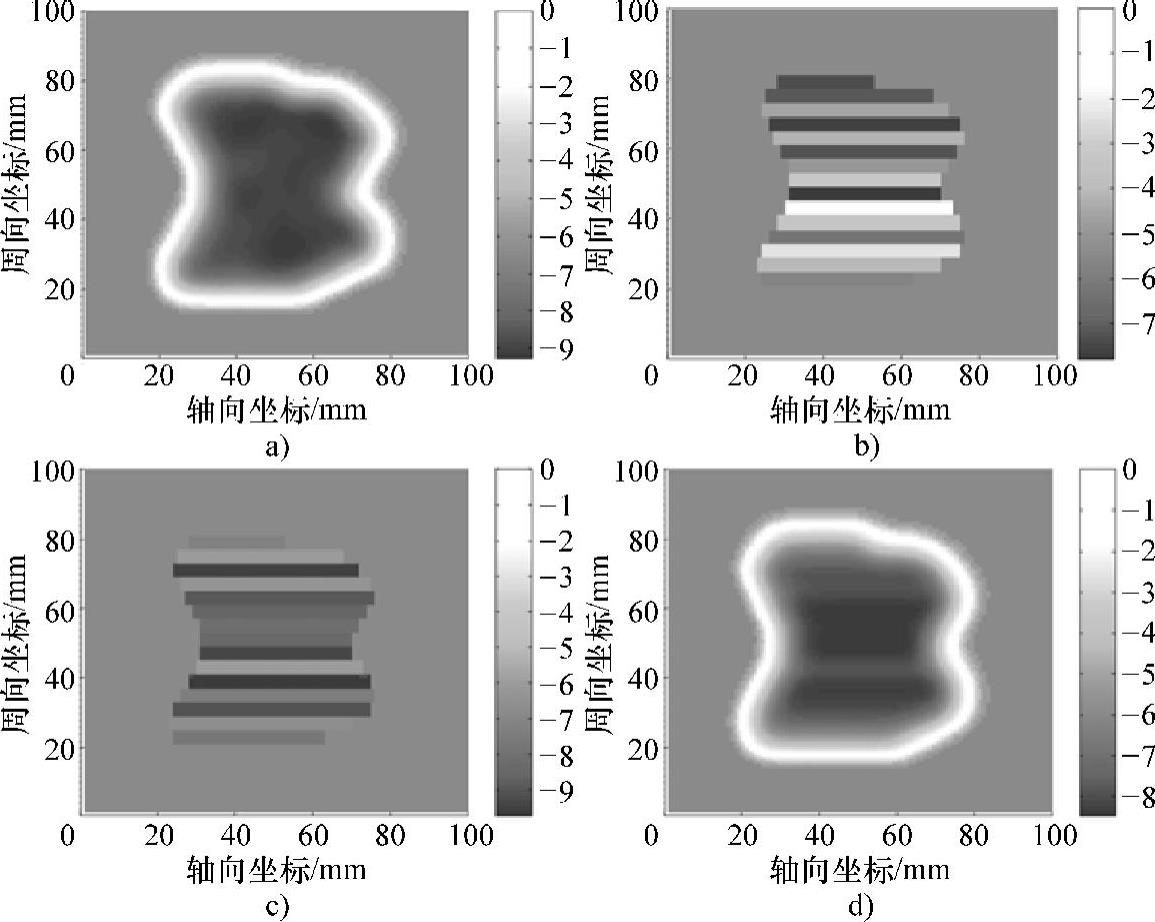
图5-76 不规则缺陷的RBF人工神经网络迭代反演
a)真实轮廓 b)由开口轮廓识别结果建立的条状模型 c)条状模型的反演结果 d)最终的缺陷轮廓
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




