磁折射及扩散分析缺陷漏磁场

铁磁性材料上的缺陷可视为材料磁特性的不连续。建立不同介质在介质分界面不连续处的磁传导模型，以计算考察磁力线在不连续处的走向情况。如图2-4所示，e是垂直于介质分界面的单位矢量，由介质1指向介质2；B₁（H₁）及B₂（H₂）分别为介质1（磁导率为μ₁）和介质2（磁导率为μ₂）内的磁感应强度（磁场强度），它们在介质1及介质2内与法线e的夹角分别为α₁、α₂。

由磁在介质分界面两侧B的法线分量连续条件，即式（2-12）可得到

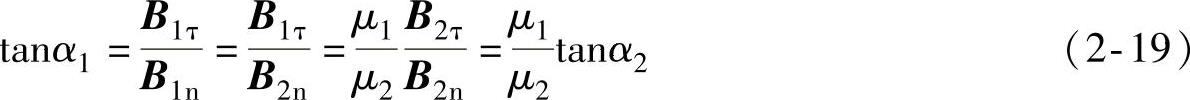
式中，B_1n（H_1n）、B_2n（H_2n）及B_1τ（H_1τ）、B_2τ（H_2τ）分别为在介质1和介质2内磁感应强度（磁场强度）的法向分量和切向分量。

式（2-19）可表示为

式（2-20）表明，磁介质分界面两侧磁感应强度与法线夹角的正切之比等于两侧材料的磁导率之比。

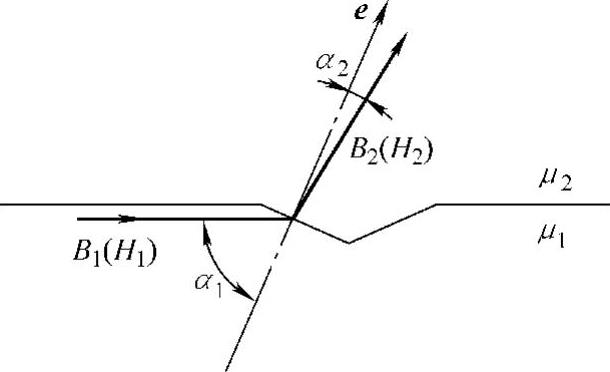
图2-4 介质分界面处的磁扩散

同样，由介质分界面两侧磁场强度H的切线分量连续条件，即式（2-15）可得到

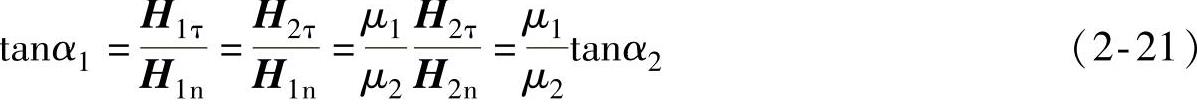
式（2-21）表明，介质分界面两侧磁场强度与法线夹角的正切之比也等于两侧材料的磁导率之比。

对于各向同性的均匀磁介质，介质中的B=μμ₀H，因而在介质中磁感应曲线与磁场强度曲线是相互平行的两组曲线，或者说它们有相同的构形。式（2-20）表明，不同的各向同性均匀介质界面的存在，并不改变B曲线和H曲线的相同构形分布。

最终，由式（2-20）得到

式（2-22）构成缺陷处的磁折射扩散规则。磁的折射偏转方向与入射角以及介质的磁导率有关。磁场方向与介质分界面几何形状构成入射角α₁。由于α₁=0°或α₁=90°的磁入射角只发生在理想的介质分界面几何形状条件下，所以结合实际的磁入射角范围0＜α₁＜90°对式（2-22）做如下讨论。

1）当μ₂=μ₁时，有α₂=α₁，磁感应线直接穿越界面不发生折射，如图2-5a所示。在同一磁场H下，由B=μH可知B₂=B₁，此时两者磁压相等，磁压差为零的情况下互不发生磁泄漏。(www.xing528.com)

2）当μ₂＜μ₁时，有α₂＜α₁，介质2内磁感应线发生折射，且折向法线e，形成磁通量由介质1向介质2的泄漏扩散，如图2-5b所示。

此时，由于B₂=μ₂H＜μ₁H=B₁，即存在着由介质1向介质2的磁压差，会形成由前者向后者的磁泄漏扩散。当介质1为铁磁性材料，介质2为空气时，最终形成由铁磁性材料向空气的磁泄漏。由于在介质分界面处突变的缺陷符合0＜α₁＜90°条件，所以这就是现有漏磁检测技术中缺陷处会发生磁泄漏的原因。

但不管怎样，因为μ₂（μ_air=1）≥1，所以

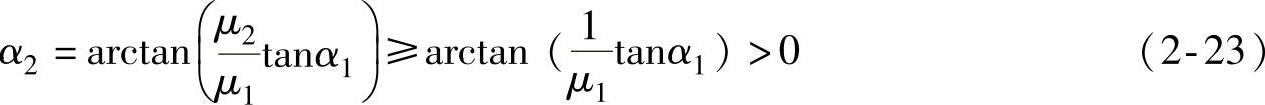
可见，由于μ₂（μ_air=1）≥1的存在，导致偏转泄漏角有最大值90°-α₂。

3）通过以上分析，可进一步假设存在介质，其μ₂→0或μ₂=0，则会得到

或

这样，磁感应线的折射线更加偏向中法线e并与之重合，发生最为极端的磁偏转折射，导致最终的磁泄漏如图2-5c所示。

此时，由于B₂=μ₂H=0，介质2内无磁力线，即对于介质1，其背景磁场呈“磁真空”状，这就形成了介质2对介质1的磁吸附作用趋势。

因此，式（2-18）可修正为

B_mfl=B_r+B_d-B_c+ΔB_r （2-26）

式中，ΔB_r为磁折射效应在清除背景磁场后的磁感应强度折射偏转增大值。

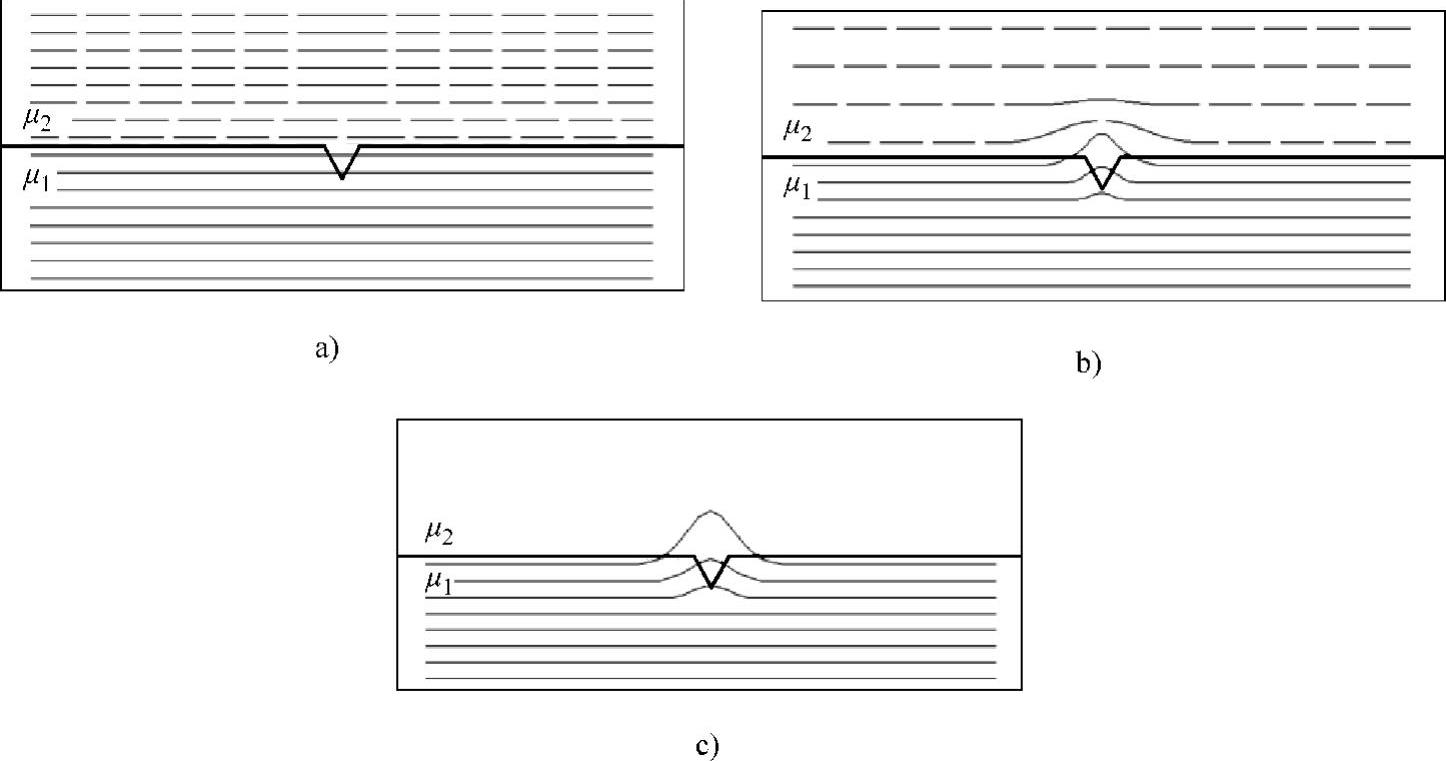
图2-5 介质1与介质2在介质分界面处的磁泄漏

a）μ₂=μ₁ b）μ₂＜μ₁ c）μ₂→0或μ₂=0