磁介质边界条件：连续的磁感应强度与磁场强度

在有磁介质存在的稳恒磁场中，磁场强度H和磁感应强度B在空间逐点变化，遵守的规律是安培环路定理和磁场高斯定理，其微分形式分别为

×H=j₀ （2-6）和

×H=j₀ （2-6）和

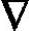·B=0 （2-7）

若磁介质为各向同性均匀磁介质，则B与H之间的关系为

B=μμ₀H （2-8）

式中，μ为介质的磁导率。

由式（2-6）和式（2-7）可得安培环路定理和磁场高斯定理的积分形式为

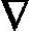·B=0 （2-7）

若磁介质为各向同性均匀磁介质，则B与H之间的关系为

B=μμ₀H （2-8）

式中，μ为介质的磁导率。

由式（2-6）和式（2-7）可得安培环路定理和磁场高斯定理的积分形式为

在两种磁介质分界面处可以做如下推导

在两种磁介质分界面处可以做如下推导

式中，n为磁介质分界面的单位法线矢量；B₁和B₂分别为磁介质1和磁介质2内的磁感应强度。

由式（2-11）可以得到

n·（B₂-B₁）=0或B_2n=B_1n （2-12）

式（2-12）表明，介质分界面两侧磁感应强度的法向分量是连续的。(www.xing528.com)

另外，由安培环路定理有

式中，n为磁介质分界面的单位法线矢量；B₁和B₂分别为磁介质1和磁介质2内的磁感应强度。

由式（2-11）可以得到

n·（B₂-B₁）=0或B_2n=B_1n （2-12）

式（2-12）表明，介质分界面两侧磁感应强度的法向分量是连续的。

另外，由安培环路定理有

由式（2-13）可得

（H₁-H₂）·τ=H_1τ-H_2τ=i₀·（τ×n） （2-14）

若介质分界面上传导电流i₀=0，继而可得

H_2τ=H_1τ （2-15）

式（2-15）表明，在两介质分界面上无传导电流时，介质分界面两侧磁场强度的切线分量连续。

所以，磁在介质分界面连续的条件为：①介质分界面两侧磁感应强度B的法向分量连续；②介质分界面两侧磁场强度H的切向分量连续。若介质分界面两侧磁介质的磁导率分别为μ₁和μ₂，则由B=μμ₀H可得介质分界面两侧B的切向分量和H的法向分量有如下关系，即

由式（2-13）可得

（H₁-H₂）·τ=H_1τ-H_2τ=i₀·（τ×n） （2-14）

若介质分界面上传导电流i₀=0，继而可得

H_2τ=H_1τ （2-15）

式（2-15）表明，在两介质分界面上无传导电流时，介质分界面两侧磁场强度的切线分量连续。

所以，磁在介质分界面连续的条件为：①介质分界面两侧磁感应强度B的法向分量连续；②介质分界面两侧磁场强度H的切向分量连续。若介质分界面两侧磁介质的磁导率分别为μ₁和μ₂，则由B=μμ₀H可得介质分界面两侧B的切向分量和H的法向分量有如下关系，即