二元函数最大值对其主要运算过程

求解下述二元函数最大值:

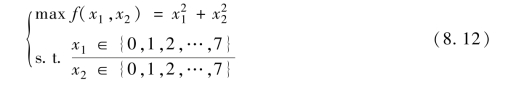
对其主要运算过程作如下解释:

(1)个体编码。GA的运算对象是表示个体的符号串，所以必须把变量x1，x2编码作为一种符号串。本例中，x1，x2取0～7之间的整数，可分别用3位无符号二进制整数来表示，将它们连接在一起所组成的6位无符号二进制整数就形成了个体的基因型，表示一个可行解。例如，基因型X＝101 110所对应的表现型是X＝[5，6]。个体的表现型x和基因型X之间可通过编码和解码程序相互转换。

(2)初始群体的产生。GA是对群体进行的进化操作，需要给其准备一些表示起始搜索点的初始群体数据。本例中，群体规模的大小取为4，即群体由四个个体组成，每个个体可通过随机方法产生。一个随机产生的初始群体如表8－2中第②栏所示。

(3)适应度计算。GA中以个体适应度的大小来评定各个个体的优劣程度，从而决定其遗传机会的大小。结合本例情况，可直接用目标函数值作为个体的适应度。为了计算函数的目标值，需对个体基因型X进行解码。表8－2中第③、④栏所示为初始群体中各个个体的解码结果，第⑤栏所示为各个个体所对应的目标函数值，也表示个体的适应度，第⑤栏还给出了群体中适应度的最大值和平均值。(www.xing528.com)

(4)选择运算。选择运算(复制运算)把当前群体中适应度较高的个体按某种规则或模型遗传到下一代群体中。一般要求适应度较高的个体将有更多的机会遗传到下一代群体中。本例中，采用与适应度成正比的概率来确定各个个体复制到下一代群体中的数量。具体操作过程是:首先计算出群体中所有个体适应度的总和∑fi；其次计算出各个个体的相对适应度的大小fi/∑fi，如表8－2中第⑥栏所示，即每个个体被遗传到下一代群体中的概率，每个概率值组成一个区域，全部概率值之和为1；最后再产生一个0～1的随机数，依据该随机数落在哪个区域内就选择哪个个体。表8－2中第⑦、⑧栏所示为一个随机产生的选择结果。

表8－2　遗传算法模拟计算

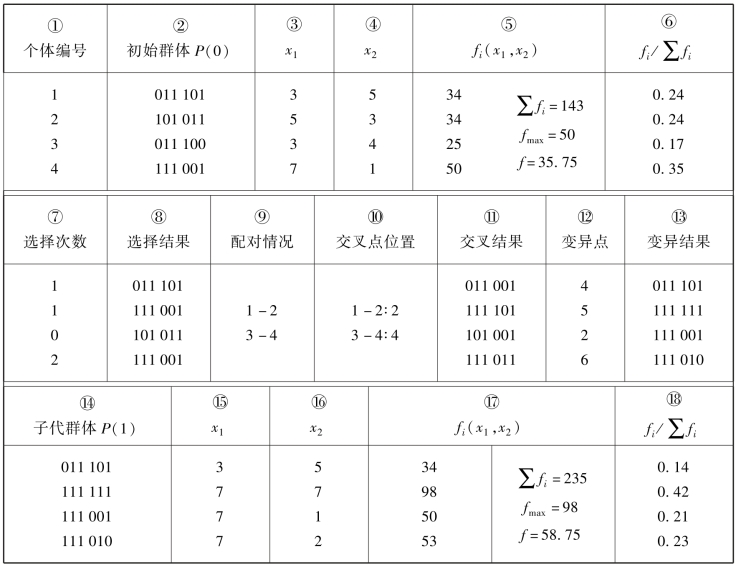
(5)交叉运算。交叉运算是GA中产生新个体的主要操作过程，它以某一个概率相互交换某两个个体之间的部分染色体。本例采用单点交叉的方法，具体操作过程是:先对群体进行随机配对，表8－2中第⑨栏所示为一种随机配对情况；其次随机设置交叉位置，表8－2中第⑩栏所示为一随机产生的交叉点位置，其中的数字表示交叉点设置在该基因座之后；最后相互交换配对染色体之间的部分基因。表8－2中第⑪栏所示为交叉运算的结果。

(6)变异运算。变异运算是对个体的某一个或某一些基因座上的基因值按某一个较小的概率进行改变，它也是产生新个体的一种操作方法。本例中，采用基本位变异的方法来进行变异运算，具体操作过程是:首先确定出各个个体的基因变异位置，表8－2中第⑫栏所示为随机产生的变异点位置，其中数字表示变异点在该基因座处；然后依照某一概率将变异点的原有基因值取反。表8－2中第⑬、⑭栏所示为变异结果。

对群体P(t)进行一轮选择、交叉、变异运算后可得到新一代的群体P(t＋1)。