多参数级联编码方法：二进制向格雷码转换公式

编码是应用GA时要解决的首要问题，它除了决定个体的染色体排列形式之外，还决定个体从搜索空间的基因型变换到解空间的表现型时的解码方法。同时，还影响到交叉算子、变异算子等遗传算子的运算方法。

De Jong曾经提出了两条可操作性较强的实用编码原则。

(1)有意义积木编码原则:应使用易于产生与问题相关的且具有低价、短定义长度模式的编码方案。

(2)最小字符集编码原则:应使用能使问题得到自然表示或描述的具有最小编码字符集的编码方案。

上述编码原则仅仅给出了设计编码方案时的一个指导性大纲，它并不适用于所有的问题。所以对于实际应用问题，仍必须对编码方法、交叉运算方法、变异运算方法和解码方法等统一考虑，以寻求到一种对问题的描述最方便、遗传运算效率最高的编码方案[5]。

1.二进制编码方法

二进制编码符号串的长度与问题所要求的求解精度有关。假设某一个参数的取值范围为[Umin，Umax]，用长度为l的二进制编码符号串来表示该参数，则它总共能够产生2l种不同的编码，若参数编码时对应关系如下:

则二进制编码的编码精度为

假设某一个体的编码是

则其解码公式为

二进制编码方法有下述一些优点:

(1)编码、解码操作简单易行。

(2)交叉、变异等遗传操作便于实现。

(3)符合最小字符集编码原则。

(4)便于利用模式定理对算法进行理论分析。

2.格雷码编码方法

二进制编码不便于反映出所求问题的结构特征，对于一些连续函数的优化问题，遗传运算的随机特性使得其局部搜索能力较差。为此，人们提出了格雷码对个体进行编码。格雷码是这样的一种编码方法，其连续的两个整数所对应的编码值之间仅仅只有一个码位是不同的，其余码位都完全相同[3]，如表8－1所示。

表8－1　二进制码与格雷码

假设有一个二进制编码为B＝bmbm－1…b2b1，其对应的格雷码为G＝gmgm－1…g2g1，由二进制编码到格雷码的转换公式为

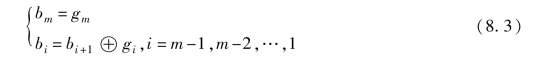
式中，⊕表示异或运算符。

格雷码有这样一个特点:任意两个整数的差是这两个整数所对应的格雷码之间的海明距离。这个特点是遗传算法中使用格雷码来进行编码的主要原因。格雷码是二进制编码方法的一种变形，其编码精度与相同长度的二进制编码的精度相同。

格雷码编码方法的主要优点如下:(www.xing528.com)

(1)便于提高遗传算法的局部搜索能力。

(2)交叉、变异等遗传操作便于实现。

(3)符合最小字符集编码原则。

(4)便于利用模式定理对算法进行理论分析。

3.浮点数编码方法

浮点数编码方法:指个体的每个基因值用某一范围内的一个浮点数来表示，个体的编码长度等于其决策变量的个数。因为这种编码方法使用的是决策变量的真实值，所以也称为真值编码方法[6]。

例如，如果某个优化问题有5个变量xi(i＝1，2，…，5)，每个变量都有对应的上下限基因型对应的表现型为x＝[5.80，6.90，3.50，3.80，5.00]T。

在浮点数编码方法中，必须保证基因值在给定的区间限制范围内，遗传算法中所使用的交叉、变异等遗传算子也必须保证其运算结果所产生的新个体的基因值也在这个区间限制范围内。再者，当用多个字节来表示一个基因值时，交叉运算必须在两个基因的分界字节处进行，而不能在某个基因的中间分隔处进行。

浮点数编码方法的优点如下:

(1)适合于在遗传算法中表示范围较大的数。

(2)适合于精度要求较高的遗传算法。

(3)便于较大空间的遗传搜索。

(4)改善了遗传算法的计算复杂性，提高了运算效率。

(5)便于遗传算法与经典优化方法的混合使用。

(6)便于设计针对问题的专门知识的知识型遗传算子。

(7)便于处理复杂的决策变量约束条件。

4.符号编码方法

符号编码方法是指个体染色体编码串中的基因值取自一个无数值含义、只有代码含义的符号集。这个符号集可以是一个字母表，如{A，B，C，…}；也可以是一个数字序列号表，如{1，2，3，…}；还可以是一个代码表，如{A1，A2，A3，…}等。

符号编码的主要优点如下:

(1)符合有意义积木编码原则。

(2)便于在遗传算法中利用所求解问题的专门知识。

(3)便于遗传算法与相近算法之间的混合使用。

5.多参数级联编码方法

将各个参数分别以某种编码方法进行编码，然后将它们的编码按一定顺序连接在一起就组成了表示全部参数的个体编码。这种编码方法称为多参数级联编码方法。在这种方法中，各个参数的编码可以是二进制、格雷码、浮点数或者符号编码等，每个参数可以具有不同的上下界、不同的编码长度或者编码精度。

6.多参数交叉编码方法

基本思想:将各个参数中起主要作用的码位集中在一起，这样它们就不易被遗传算子破坏。在进行多参数交叉编码时:首先对各个参数进行分组编码(假设共有n个参数，每个参数都用长度为m的二进制编码串来表示)；然后取各个参数编码串中的最高位连接到一起，以它们作为个体编码串的前n位编码。

多参数交叉编码方法特别适合于各个参数之间的相互关系较强、各个参数对最优解的贡献相当时的优化问题。