使用贝叶斯信念网络的推理示例

假设对使用图5－2的贝叶斯信念网络(Bayesian Belief Networks，BBN)诊断一个人是否患有心脏病感兴趣，下面介绍在不同的情况下如何做出诊断。

情况一　没有先验信息

在没有任何先验信息的情况下，可以通过计算先验概率P(HD＝Yes)和P(HD＝No)确定一个人是否可能患有心脏病。为了表述方便，设α∈{Yes，No}表示锻炼的两个值，β∈{健康，不健康}表示饮食的两个值。

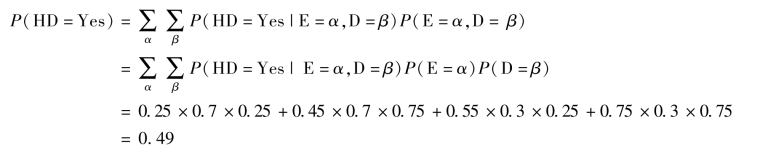
因为P(HD＝No)＝1－P(HD＝Yes)＝0.51，所以此人不得心脏病的概率略微大一点。

情况二　高血压

如果一个人有高血压，可以通过比较后验概率P(HD＝Yes｜BP＝高)和P(HD＝No｜BP＝高)诊断他是否患有心脏病。因此，必须计算P(BP＝高):

式中，γ∈{Yes，No}。(www.xing528.com)

因此，此人患心脏病的后验概率为

同理，P(HD＝No｜BP＝高)＝1－0.803 3＝0.196 7。因此，当一个人有高血压时，他患心脏病的危险就增加了。

情况三　高血压、饮食健康和经常锻炼身体

假设得知此人经常锻炼身体并且饮食健康，这些新信息会对诊断造成怎样的影响呢?加上这些新信息，此人患心脏病的后验概率为

而此人不患心脏病的概率为

P(HD＝No｜BP＝高，D＝健康，E＝Yes)＝1－0.586 2＝0.413 8

因此，模型暗示健康的饮食和有规律的体育锻炼可以降低患心脏病的危险。