朴素贝叶斯分类器：基本方法与后验概率计算

设输入空间χ⊆Rn为n维向量的集合，输出空间为类标记集合y＝{c1，c2，…，cK}。输入为特征向量x∈χ，输出为类标记y∈Y。X是定义在输入空间上的随机变量，Y是定义在输出空间Y的随机变量。P(X，Y)是X和Y的联合概率分布。训练数据集:T＝{(x1，y1)，(x2，y2)，…，(xN，yN)}由P(X，Y)独立同分布产生。

朴素贝叶斯法通过训练数据集学习联合概率分布P(X，Y)。具体地，学习以下先验概率分布及条件概率分布。先验概率分布:

条件概率分布:

于是学习到联合概率分布P(X｜Y)。

条件概率分布P(X＝x｜Y＝ck)有指数级数量的参数，其估计实际是不可行的。事实上，假设x(j)可取值有Sj个(j＝1，2，…，n)，Y可取值有K个，那么参数个数为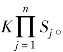朴素贝叶斯法对条件概率分布作了条件独立性的假设。由于这是一个较强的假设，朴素贝叶斯也由此得名。具体地，条件独立性假设为

朴素贝叶斯法实际上学习到生成数据的机制，所以属于生成模型。条件独立假设用于分类的特征在类确定的条件下都是条件独立的。这一假设使朴素贝叶斯法变得简单，但是有时会牺牲一定的分类准确率[2]。(www.xing528.com)

朴素贝叶斯法分类时，对给定的输入x，通过学习到的模型计算后验概率分布P(Y＝ck｜X＝x)，将后验概率最大的类作为x的类输出[3]。后验概率计算根据贝叶斯定理进行:

将条件独立性假设代入式(5.4)后，有

这就是朴素贝叶斯法分类的基本公式。于是，朴素贝叶斯分类器可表示为

在式(5.6)中分母对所有ck都是相同的，则