为了便于说明，首先给出熵与条件熵的定义。在信息论与概率统计中，熵是表示随机变量不确定性的度量。设X是一个取有限个值的离散随机变量，其概率分布为
P(X＝xi)＝pi，i＝1，2，…，n
随机变量X的熵定义为
在式(4.1)中，若pi＝0，则定义0log 0＝0。通常，式中的对数以2为底数或以自然对数e为底数，这时熵的单位分别称为比特或纳特。由定义可知，熵只依赖于X的分布，而与X的取值无关，所以也可将X的熵记为H(p)，即
熵越大，随机变量的不确定性就越大。从定义可验证:
0≤H(p)≤log n
当随机变量只取两个值，即1、0时，X的分布为
P(X＝1)＝p，P(X＝0)＝1－p，0≤p≤1
熵为
这时，熵H(p)随概率p变化的曲线如图4－3所示(单位为bit)。
当p＝0或p＝1时，H(p)＝0，随机变量完全没有不确定性。当p＝0.5时，H(p)＝1，熵取值最大，随机变量不确定性最大[3]。
设有随机变量(X，Y)，其联合概率分布为
图4－3 分布为伯努利分布时熵与概率的关系
P(X＝xi，Y＝yi)＝pij，i＝1，2，…，n；j＝1，2，…，m(www.xing528.com)
条件熵H(Y｜X)表示在已知随机变量X的条件下随机变量Y的不确定性。随机变量X给定的条件下随机变量Y的条件熵H(Y｜X)，定义为X给定条件下Y的条件概率分布的熵对X的数学期望:
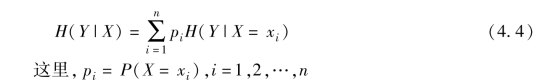
当熵和条件熵中的概率由数据估计(特别是极大似然估计)得到时，所对应的熵与条件熵分别称为经验熵和经验条件熵。此时，如果有0概率，令0log 0＝0。
信息增益表示得知特征X的信息而使得类Y的信息的不确定性减少的程度。
定义4.2信息增益:特征A对训练数据集D的信息增益g(D，A)，定义为集合D的经验熵H(D)与特征A给定条件下D的经验条件熵H(D｜A)之差，即
一般地，熵H(Y)与条件熵H(Y｜X)之差称为互信息。决策树学习中的信息增益等价于训练数据集中类与特征的互信息。
决策树学习应用信息增益准则选择特征。给定训练数据集D和特征A，经验熵H(D)表示对数据集D进行分类的不确定性，而经验条件熵H(D｜A)表示在特征A给定的条件下对数据集D进行分类的不确定性。那么它们的差，即信息增益，就表示由于特征A而使得对数据集D的分类的不确定性减少的程度。显然，对于数据集D而言，信息增益依赖于特征，不同的特征往往具有不同的信息增益。信息增益大的特征具有更强的分类能力[4]。
根据信息增益准则的特征选择方法是:对训练数据集(或子集)D，计算其每个特征的信息增益，并比较它们的大小，选择信息增益最大的特征。设训练数据集为D，｜D｜表示其样本容量，即样本个数。设有K个类Ck(k＝1，2，…，K)，｜Ck｜为属于类Ck的样本个数，
｜＝｜D｜。设特征A有n个不同的取值{a1，a2，…，an}，根据特征A的取值将D划分为n个子集D1，D2，…，Dn，｜Di｜为Di的样本个数，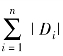
｜＝｜D｜。设子集Di中属于类Ck的样本的集合为Dik，即Dik＝Di∩Ck，｜Dik｜为Dik的样本个数。于是信息增益的算法如下。
算法4.1 信息增益的算法
输入:训练数据集D和特征A；
输出:特征A对训练数据集D的信息增益g(D，A)。
(1)计算数据集D的经验熵H(D):
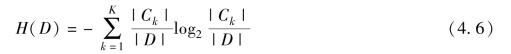
(2)计算特征A对数据集D的经验条件熵H(D｜A):
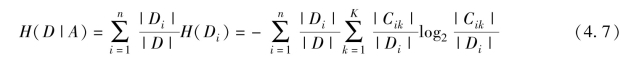
(3)计算信息增益:
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
