数据的相互独立性：定义与影响

数据相互独立，即m≠n。

1.两组数据方差相等

与数据成对的情形相似，仍可采用t检验的方式。我们观察的数据如下:

{Xi，i＝1，2，…，n}～N(0，1)

{Yj，j＝1，2，…，m}～N(0，1)

两者皆独立同分布。

已知用μD＝μx－μY进行归一化，用总体的方差，作为σ2的估计量。

其中，

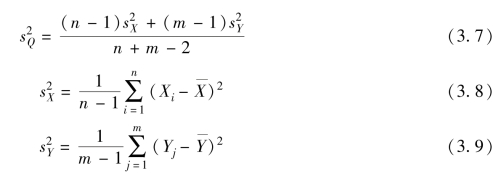
而基于概率论的知识，可得

同样地，使用检验统计量:

对应的假设检验和置信区间如表3－6所示。

表3－6　数据独立且方差相等时各检验方法的置信区间

已知使用加权方法估计总体分布的方差，有

(www.xing528.com)

此处采用的检验统计量为

式中:γ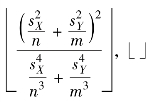＝表示向下取整。假设检验方法可参考前述情形类推得到。

2.两组数据方差不等

两组数据方差不等，可使用Mann－Whitney检验方法。

第一组的数目记为n1，第二组的数目记为n2，将它们合并进行排序，得到第一组的序号和A1，第二组的序号和为A2。若数据相等，则求其序号平均值再赋回。

令

注意，U2＋U2＝U1U2＝n1n2。

检验统计量为U:第一组的中位数减去第二组的中位数。

当数据量小(n1，n2≤10)时，假设检验方法如表3－7所示。

表3－7　数据独立且方差不等时各检验方法的流程

当数据量大(n1，n2＞10)时，可采用检验统计量进行估计:

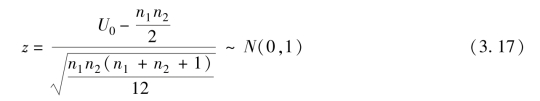
各假设检验的原假设和备择假设不变。注意，由于U0＝min{U1，U2}，故z＜0。