数据成对的数学表达法及其检验方法

数据成对的数学表达，即n＝m。

1.两组数据方差相等

此时需要评估两组数据的分布均值的差异，使用t分布进行估计。由于数据成对，因而能通过分析{Di＝Xi－Yi，i＝1，2，…，m}的分布完成估计。记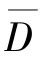为{Di＝Xi－Yi，i＝1，2，…，m}的均值。

按照3.1节中方差未知的情况，用μD＝μ1－μ2进行归一化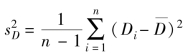，作为的估计量。同样地，使用检验统计量为

对应的假设检验和置信区间如表3－4所示。

表3－4　两组数据方差相等时各检验方法的置信区间

续表

2.两组数据方差不等

当两组数据方差不等时，需要用到非参数方法中的符号检验法和Wilcoxon秩检验法。下面介绍参数方法和非参数方法的概念。若已有的总体分布已知或可以假设，则其中只有已知个数的未知量待估计。基于样本对这些参数进行估计或假设检验的方法即参数化方法。在实际问题中，对实际数据的总体分布我们所知甚少。不假设分布的总体形式，基于样本本身的信息进行统计的方法为非参数方法。非参数化方法对分布形式要求低，故普适性好。但是由于针对性不足，故有效性相对参数化方法一般有所欠缺。

(1)符号检验法:该方法仅考虑{Di＝sig n(Xi－Yi)，i＝1，2，…，n}中不为0的个体的分布，共有n个元素，适用于数据间差距“正常”的情况。

当数据较少(少于等于25个样本，即n≤25)时，可以设

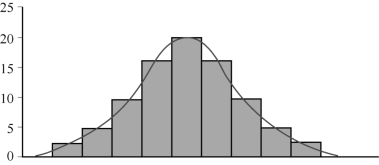
1/2即数据“正常”的数学表达。Di服从二项式分布(n，1/2)，如图3－1所示，各检验方法与置信区间的获取如表3－5所示。

(www.xing528.com)

图3－1　数据的二项式分布

表3－5　方差不等的各检验方法的流程

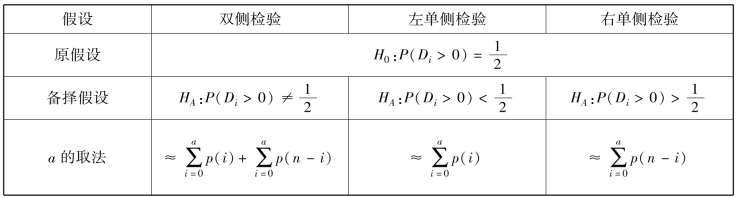
当数据规模较大(多于25个样本)时，可以用检验统计量:

注意，此时的＃(Di＞0)指Di＞0的个数，n/2为均值，估计方法如上所述。

(2)Wilcoxon秩检验法:该方法适用于数据间差距不正常的情况。对于非正态分布或不能从数量上精确度量的数据，秩方法具有独特的优越性。

检验统计量z的获取方法如下:

Di＝Xi－Yi，i＝1，2，…，n

A＋＝满足Di＞0的排序序号之和

A－＝满足Di＜0的排序序号之和

A0＝min{A＋，A－}

注意到A＋＋A－＝n(n＋1)/2，则在样本个数大于5的情况下，得到检验统计量:

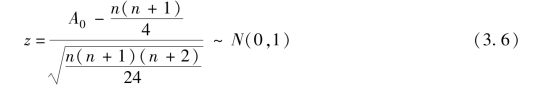
基于正态分布的检验统计量的假设检验方法之前已经介绍过，此处不再赘述。