吊钩质量mh、负载质量mp、悬索长度ls、吊索长度lg、负载长度lp、距离b 分别选择50 kg、2 000 kg、15 m、7 m、10 m、5 m。仿真条件:首先加速直升机向前飞行沿Ny方向移动,然后将飞行速度保持在恒定值46 km/h。在行程结束时,直升机减速停在目标位置,距离3.2 km。图8.3~图8.6 给出了对应的仿真结果。
图8.3 给出了直升机姿态的仿真结果。模型跟踪控制器作用下,直升机姿态的峰-峰振幅是7.5°。模型跟踪控制器和光滑器复合作用下,直升机姿态的峰-峰振幅是5.5°。直升机姿态的过渡过程时间被定义为残余响应进入0.5°所需要的时间。模型跟踪控制器作用下,过渡过程时间是219.1 s。模型跟踪控制器和光滑器复合作用下,过渡过程时间是11.9 s。因此,复合控制方法可以消减更多的直升机姿态振荡。另外,直升机姿态的振荡频率小于模型跟踪控制器的设计频率和负载摆动的第一模态频率,这是因为直升机与吊挂负载之间存在复杂的耦合效果。
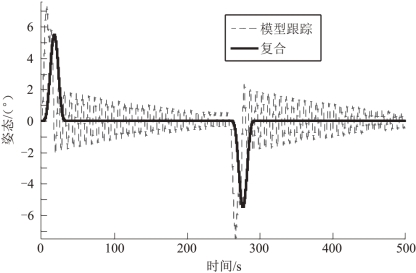
图8.3 直升机姿态响应
图8.4 给出了负载质心偏移量仿真响应图。模型跟踪控制器作用下,负载质心偏移量的峰-峰振幅是3.6 m,过渡过程时间是173.5 s。负载质心偏移量的过渡过程时间被定义为残余响应进入0.01(ls+ly)范围内所需要的时间。模型跟踪控制器和光滑器复合作用下,负载质心偏移量的峰-峰振幅是1.8 m,过渡过程时间是7.1 s。因此,模型跟踪控制器和光滑器复合控制方法消减了更多的负载振荡。另外,图8.4中负载偏移量的振荡频率与图8.3中直升机姿态的振荡频率相等,这是直升机与负载振荡之间耦合作用的结果。
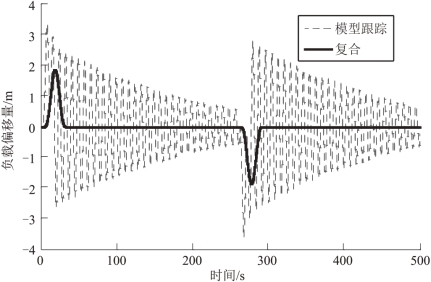
图8.4 负载振荡偏移量响应(https://www.xing528.com)
图8.5 给出了负载扭转速度和加速度的仿真响应曲线。在模型跟踪控制作用下,局部极小值点出现在扭转角速度曲线中的30 s、200 s和360 s附近。同时,局部极大值点出现在100 s 和300 s 附近。这是由于加减速引起振荡时而同相、时而反相的结果。扭转速度曲线在局部极大和局部极小点以后会趋向于恒定数值,这是由于负载扭转的频率取决于负载摆动的振幅。模型跟踪控制器作用下,扭转速度的残余振幅是0.37°/s。在模型跟踪控制器和光滑器复合作用下,扭转速度的残余振幅是0.08°/s。复合控制方法将扭转速度抑制到非常低的程度,有助于安全运载。
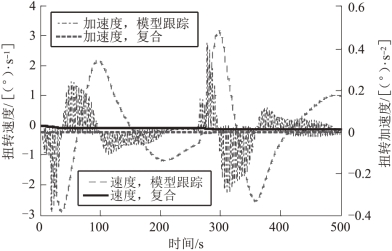
图8.5 负载扭转速度和加速度的仿真响应曲线
图8.6给出了旋翼角的仿真响应。在模型跟踪控制器作用下,旋翼角峰-峰振幅是0.78°。在模型跟踪控制器和光滑器复合作用下,旋翼角峰-峰振幅是0.039°。图8.6 中旋翼角频率与图8.3 直升机姿态频率、图8.4 负载振荡频率相同。这是因为直升机和负载之间的耦合作用,通过调节旋翼角产生了直升机姿态的阻尼效果。
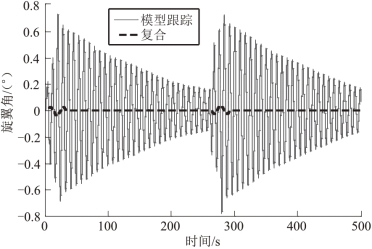
图8.6 旋翼角的仿真响应
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




