液深90 mm下容器运动的动力学响应及振幅分析

图6.11 所示为液体三维晃动示意图。长度为a、宽度为b 的矩形容器内充有液深为h 的液体。η 代表从静止液面量起的液面高度，容器运动可以分解为沿着固定坐标系X'、Y'两个方向的线性运动，C（t）为容器运动加速度，α 为加速度方向与X'方向的夹角。Oxy 为移动坐标系，固结于液体静止液面上，坐标系原点在容器转角处，动坐标系与惯性坐标系的方向平行。

假设贮液箱内液体是不可压缩的、无黏性的，贮液箱内流体的流动是无旋的，并且自由液面的波高和速度相对较小，容器是刚性的、不可渗透的。对于无旋流动，容器内液体速度可写为：

式中，v0为贮液箱的运动速度；∇为梯度算子；φ为扰动速度势。则贮液箱内液体自由晃动的边界值问题在动坐标系中可描述为：

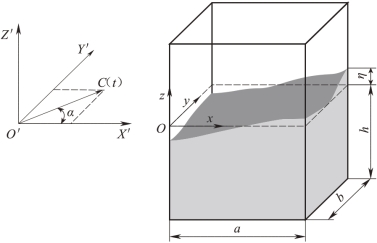
图6.11　矩形容器三维晃动物理模型

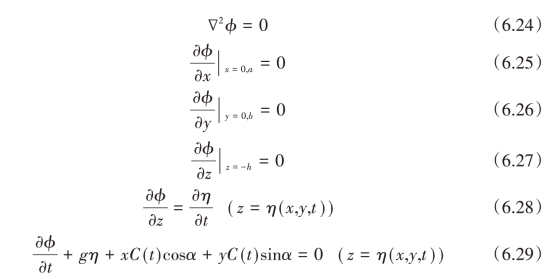
式中g为重力加速度，扰动速度势函数φ和液高η可以写成如下形式：

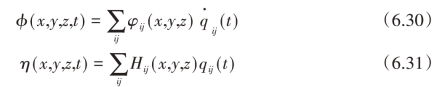
式中，i、j 为非负数；qij（t）为时间相关的函数；φij（x，y，z）和Hij（x，y，z）是对应的空间函数，它们是如下方程组的解：

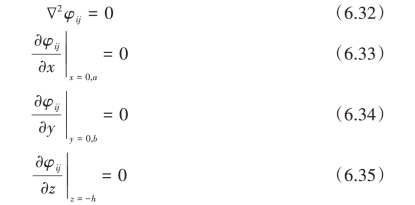
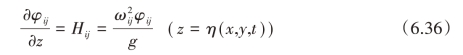
解方程（6.32）～方程（6.36），得到液体晃动的自然频率ωij以及对应的模态函数：

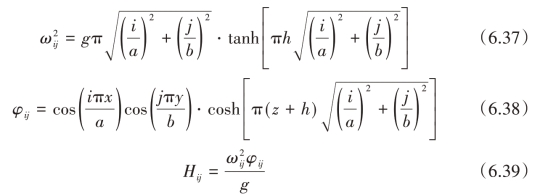
式中，i、j 为整数，并且ωi0、ω0j和ωij分别是横向模态、纵向模态和混合模态。将方程（6.30）和方程（6.31）代入方程（6.29），两边同时乘以φij，再在自由液面（0 ≤x ≤a；0 ≤y ≤b）上进行积分，得到受迫晃动方程：

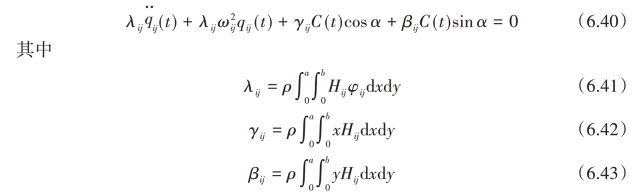
式中，ρ为液体密度。根据方程（6.42）和方程（6.43）计算γijx和βijy的值得到：

方程（6.44）和方程（6.45）表明，横向激励只能激发横向晃动模态，纵向激励只能激发纵向晃动模态，平面两个方向的激励不能激发混合晃动模态。考虑系统阻尼，则式（6.40）可以写成如下形式：

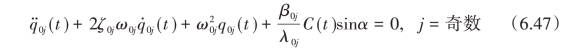
上式中ζi0和ζ0j分别是横向晃动模态的阻尼和纵向晃动模态的阻尼，对于水，各个模态的晃动阻尼约为0.01。将式（6.39）代入式（6.31）中得到任意测量点处的液高表达式为：(www.xing528.com)

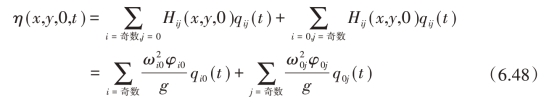
由式（6.46）～式（6.48）可得容器对角处液高与外界激励之间的传递函数为：

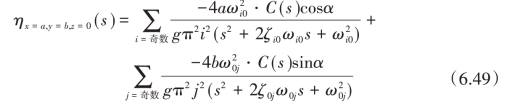
此外，将式（6.38）、式（6.46）、式（6.47）代入式（6.30）中，可得容器对角处液体扰动速度势与外界激励传递函数之间的关系为：

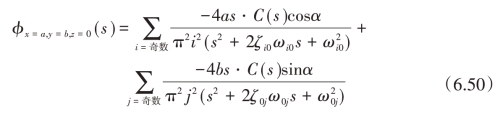
理论分析显示，容器内液体晃动液高和扰动速度势是两个方向无数个晃动模态的叠加，但是在平面运动激励下，两个方向的晃动是相互独立的，横向模态与纵向模态之间没有耦合。由式（6.49）可得脉冲激励下，贮液箱对角处液体晃动所有模态振幅为：

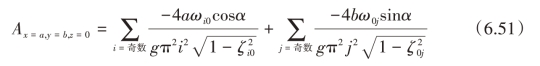
引入脉冲激励下每个方向各个晃动模态与对应方向基础晃动模态的振幅之比，来表征单个晃动模态对整个系统动力学的影响，这个比值称为相对振幅贡献率，基于此概念，式（6.51）可以写作如下形式：

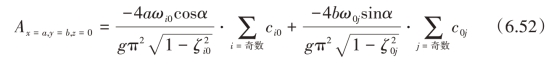
式中，ωi0和ζi0为横向基础晃动模态的固有频率和阻尼比；ω0j和ζ0j为纵向基础晃动模态的固有频率和阻尼比；ci0和c0j分别为横向与纵向的相对振幅贡献率，具体形式可写作：

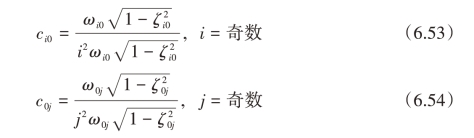
因此，贮液容器对角处液体所有晃动模态振幅之和为各方向基础晃动模态振幅乘以相对振幅贡献率之和。

图6.12给出了液深90 mm 时，各个晃动模态的相对振幅贡献，其余的仿真参数在表6.2中列出，由图可以看出，横向的第三模态、第五模态、第七模态的振幅贡献率分别为20.1%、9.4%和5.6%。对于纵向模态，第三模态、第五模态、第七模态的振幅贡献率分别为19.3%、9.0%和5.4%。仿真分析，横向的第九模态到第十九模态相对振幅贡献之和为13.5%，纵向的第九模态到第十九模态的相对振幅贡献之和为13.0%。这表明高阶模态的振动对系统的动力学有明显的影响，在设计控制方法时，必须考虑抑制高阶模态的振动。

图6.12　相对振幅贡献

表6.2　仿真/实验参数

容器运动的原始驱动命令为梯形速度命令，系统的动力学响应可以分为两个阶段：瞬态响应阶段和残余振动阶段。瞬态响应阶段指的是容器处于运动状态的时间段，在这个时间段内液体晃动的峰-峰振幅为瞬态振幅；残余阶段指的是容器运动停止后的时间段，在此段时间内的液体晃动峰-峰振幅为残余振幅，分别用两个时间段内峰-峰振幅的大小来衡量液体振动的剧烈程度。

图6.13 所示为液深90 mm，驱动距离为20 cm，驱动角为30°时，横、纵向晃动响应以及全模态响应，仿真分析了前十个模态的影响。横向模态、纵向模态和全模态的瞬态振幅分别为29.1 mm、16.3 mm 和41.6 mm。对于三者的残余振幅，其大小分别为15.7 mm、17.3 mm 和29.4 mm。仿真结果显示，整个系统的响应是两个方向振动响应的叠加，两个方向的基础晃动模态和高阶模态都对整个系统的动力学影响显著，这要求控制器必须能够抑制全模态振动。

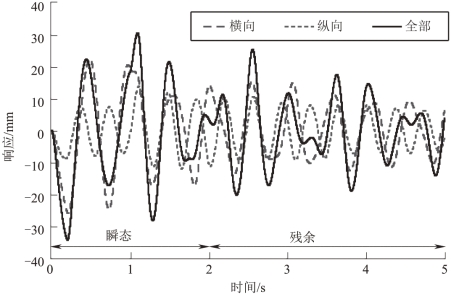
图6.13　两个方向上的晃动响应