液面动力学特性分析与振动模态分析

图6.1 所示为液体二维晃动的示意图，矩形容器的长度为2a，内部充有液面高度为h 的液体，η 表示晃动时自由液面到静止液面的高度，容器的侧向加速度为C（t），为了简化动力学建模，作以下假设：

（1）流体流动是无旋的；

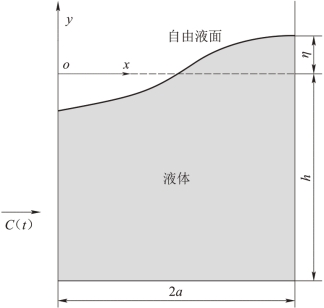
图6.1　平面液体晃动物理模型图

（2）容器内流体是无黏性、均匀、不可压缩的；

（3）容器是绝对刚性的，没有弹性变形；

（4）液体晃动是微幅晃动。

对于无旋流动，容器中流体的速度可表示为：

式中，v0为容器的速度；∇是梯度算子；φ 是扰动速度势函数。通过上述假设，自由液面的晃动边界值问题可描述为：

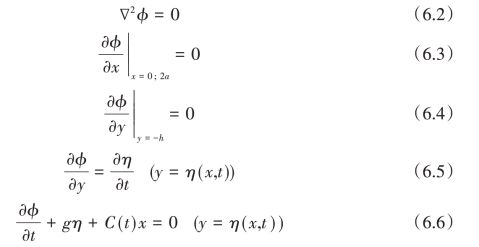
其中g为重力加速度。扰动速度势函数φ和液高η可表示为：

式中，qk（t）是关于时间的函数；φk（x，y）和Hk（x，y）是对应的模态函数。它们是下列边界值问题的解：

解方程（6.9）～方程（6.12），得到各个晃动模态的固有频率ωk及对应的空间函数φk和Hk：

(www.xing528.com)

前人文献表明，式（6.13）可以用来估计液体晃动频率。把式（6.7）、式（6.8）代入式（6.6）中，然后两边同时乘以φk 并在自由液面上（0 ≤x ≤2a）积分，得到：

式中，ρ 为液体的密度。当k 为偶数时，αk等于零，这说明横向加速度C（t）只能激发奇数晃动模态响应，偶数晃动模态不被激发。实际液体晃动具有耗散性，引入系统阻尼表征晃动的耗散性，又因为偶数晃动模态不被激发，因此式（6.16）可以整理成如下形式［159］：

式中，ζk为各个晃动模态的阻尼比，阻尼比的理论表达式是一个实验常数、Galilei 数和容器形状的函数，对于水，各个模态的晃动阻尼比约为0.01。把式（6.15）代入式（6.8）中可以得到自由液面上任意测量点处的液高为：

因此，液面高度为无穷晃动模态响应的总和。从式（6.19）和式（6.20）可以得到容器最右侧处液高与外界激励之间的传递函数：

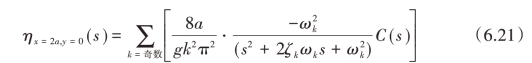
另外，把式（6.14）和式（6.19）代入式（6.7），可以得到容器最右侧处扰动速度势与外界激励之间的传递函数：

模型方程（6.21）和模型方程（6.22）包含无穷晃动模态，因此系统总响应为各个晃动模态响应的叠加。为了研究高阶模态的影响，引入相对振幅贡献概念，其定义为脉冲响应下的高阶模态的振幅与基础模态的振幅比，用此比值来评估高阶晃动模态对整个系统的影响。

图6.2所示为液深大范围变化时，各个高阶模态相对振幅贡献的变化情况。在50 mm深度以前，随着液体深度的增加，相对振幅贡献下降；液深超过50 mm后，随着液深变化，相对振幅贡献趋于平缓。第三模态，第五模态和第七模态的平均相对振幅的贡献分别为19.8%、9.2%、5.6%，第九模态到第十九模态的平均振幅相对贡献为12%。仿真结果显示高阶模态对整个系统的动力学有显著影响，因此需要设计一种控制方法能够有效地抑制液体全部模态的晃动。

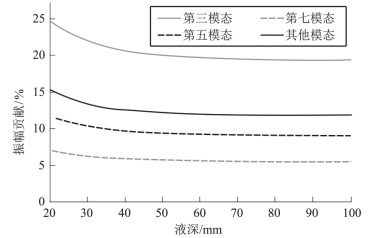
图6.2　高阶模态相对振幅贡献

容器运动的原始驱动命令为梯形速度命令。表6.1 给出了本节中使用的仿真与实验参数。系统的响应按照时间可划分为两个阶段：瞬态响应阶段与残余响应阶段。瞬态响应阶段指的是容器运动过程中，系统的动力学响应，在此时间段内的峰-峰振幅定义为瞬态振幅；残余响应阶段定义为容器停止运动以后的时间范围，此时间段内振动的峰-峰振幅定义为残余振幅。分别用瞬态振幅和残余振幅来表征瞬态振动和残余振动的剧烈程度。

表6.1　仿真参数