无穷达芬振子模型下的梁动力学研究

方程（5.1）仍然可以描述此种情况下的力平衡。同样，力矩平衡仍然可以使用方程（5.2）描述。由梁的弯曲基本理论，可以将梁的弯矩表示为：

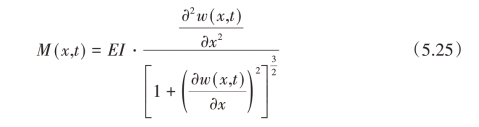
式中，E为杨氏模量；I为沿横截面的惯性矩。对式（5.25）进行泰勒展开然后忽略高阶项后得到：

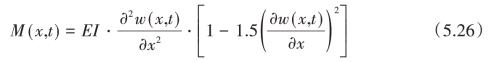
将式（5.26）代入式（5.2），然后代入式（5.1），接着忽略dx 的高阶成分后得到：

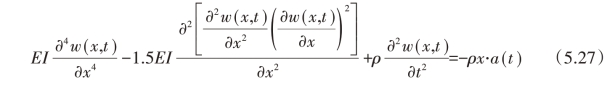
单连杆柔性机械臂的边界条件可以表示为：

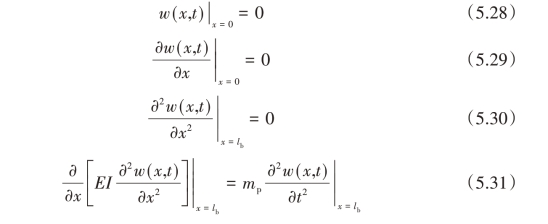
其中边界条件（5.28）表明在驱动轮毂处梁的挠度为零，边界条件（5.29）表示挠度函数对位置的偏微分也为零。而边界条件（5.30）表示梁端部的弯矩为零，边界条件（5.31）表示梁端部的剪切力满足的边界条件。柔性机械臂由驱动命令引起的振动可以通过模态叠加的方法决定。在这种情况下梁的挠度可以表示为各个模态的线性叠加：

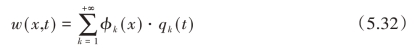
式中，φk（x）是模型的第k阶振动模态的振型函数；qk（t）是相应的时间函数。通过求解式（5.28）～式（5.32），我们可以得到系统的线性频率ωk和振型函数φk（x）：

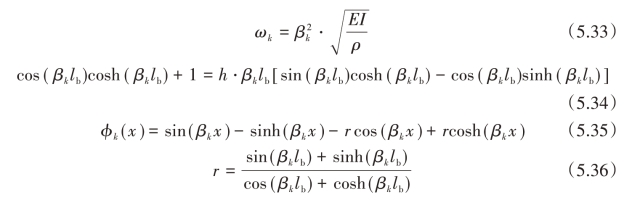
式中，ωk为第k阶模态的自然频率；h是负载质量和梁的质量之比；参数βk由于具有非线性，很难求得解析解，然而通过其他已知参数我们能求得它的数值解。将式（5.32）代入式（5.27），然后忽略模态之间的耦合项，可以得到：

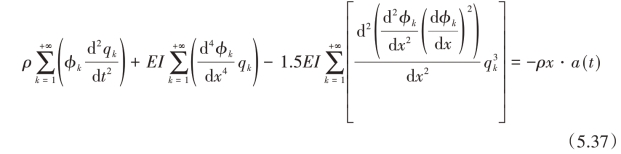
等式两边同时乘以φk（x），然后对其在0 ≤x ≤lb上进行积分处理可得：(www.xing528.com)

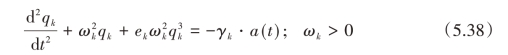
式中，ek为第k阶模态的非线性刚度系数，参数ek和γk的表达式如下：

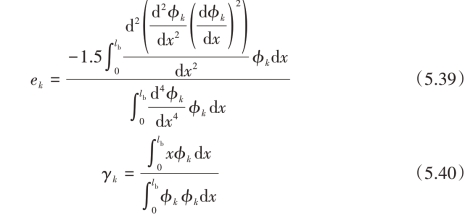
对式（5.38）加入比例阻尼项可以得到近似的响应方程：

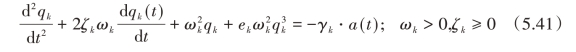
式中，ζk为第k阶模态的阻尼比。该模型方程（5.41）是包含了无穷个达芬振子的模型，它的时间响应可以近似表示为其中每个达芬振子响应的线性叠加。

为了验证模型的正确性以及研究模型的动力学特性，做出了如下的仿真和实验。表5.2 所示为模型选取的仿真参数，轮毂的驱动命令选取为梯形速度命令，选取了模型的前四阶模态，并给出了驱动距离为54°时的仿真和实验图像，如图5.14所示。从图中可以看出，线性模型和非线性达芬模型的响应曲线和实验响应曲线有着相近的变化趋势，当时非线性达芬模型的响应曲线和实验的响应曲线更为接近。其中轮毂的驱动时间段为0～2.7 s，实验响应的瞬态振幅为186.1 mm，残余振幅为338.7 mm。该曲线证明了我们建立的达芬模型的正确性，并且模型相比线性模型更加精确。

表5.2　模型仿真参数

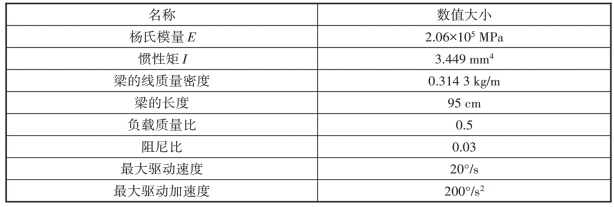
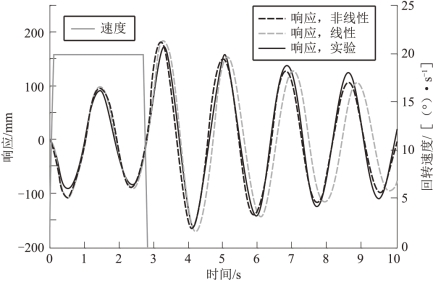
图5.14　仿真和实验响应

图5.15所示为第一模态非线性刚度系数作为负载质量比和梁的长度的函数的图像。从图中可以看出，随着梁的长度的增加，非线性刚度系数的幅值大小减小。且在负载质量比小于0.07时，非线性刚度系数一直为负值，此时表现为软弹簧的性质；而负载质量比大于0.07 时，非线性刚度系数为正值，此时表现为硬弹簧的性质。非线性刚度系数随着负载质量比的增加而增加，在负载质量比达到1.16时增加到一个最大值，然后随着负载质量比的增加而减小。

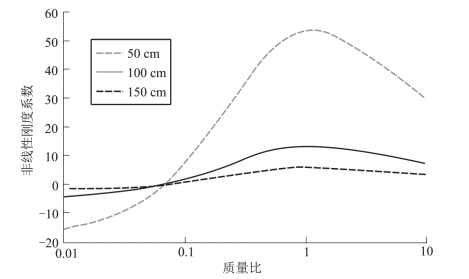
图5.15　第一模态非线性刚度系数随质量比和连杆长度的变化