塔式起重机光滑控制器实验验证

在图4.1所示实验台上进行动力学行为验证和光滑器振荡控制效果验证。小车在横梁位置固定在75 cm处，一个网球和一个细长梁被用作吊钩和负载，悬索和吊索都使用大力马钓鱼线，吊钩质量、负载质量、负载长度、悬索长度和吊索长度设置为32 g、155 g、29.7 cm、54 cm和16 cm。

为了检测负载上两个标记的位移，横梁上安装了摄像机。摄像机的摄像速率为每秒钟30帧。两个标记的位移用来检测负载摆动位移和扭转角。对两个标记位移求平均可以得到负载摆动的位移。负载扭转角速度可以用反正切函数来求得。

图4.6展示了塔式起重机带光滑控制器整体控制结构。信号控制接口产生一个原始的梯形速度命令，然后经由光滑器光滑处理后，生成一个光滑的速度命令，该整形后的命令便可以驱动电机旋转臂或者移动小车，实现抑制负载残余摆动和扭转运动的作用。通过使用起重机的四个固定参数：悬索长度ls、吊索长度lr、分布质量细长梁长度lp和质量比c，然后应用起重机第一摆动频率公式来计算光滑器的设计频率，从而设计两段光滑器。

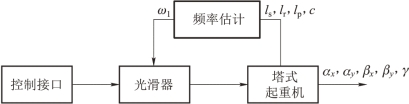
图4.6　塔式起重机控制框图

图4.7为电机驱动80°驱动距离下有无光滑控制器作用时负载质心摆动轨迹对比图。横坐标和纵坐标分别代表负载质心的径向振幅（即沿着吊臂方向）和切向振幅（即垂直吊臂方向）。图中坐标原点代表负载质心的静止平衡点。无控制器作用时，负载质心最大残余摆动量的实验值与仿真值分别为105.66 mm和95.27 mm，而在光滑控制器作用下，负载摆动的实验值和仿真值分别为9.87 mm和0.95 mm。从数据上分析，光滑器很好地抑制了负载的残余摆动，实验和仿真抑制率为90.66%和99.00%。从图中的光滑器作用后的轨迹图可以看出，负载质心的摆动像是被限制在原点附近作小幅度的摆动运动。从此图可以得出结论，80°驱动角度下，光滑器可以很好地抑制负载的残余摆动，抑制比也超过90%。

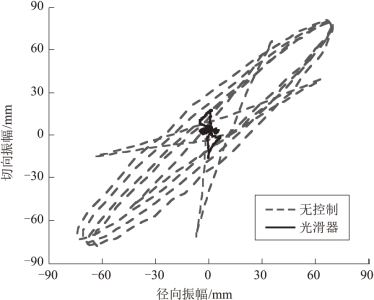
图4.7　负载摆动实验响应

图4.8为电机驱动80°驱动距离下有无光滑控制器作用时负载残余扭转速度对比图。没有控制器作用时，负载的扭转运动的瞬态阶段近似为0 s到4 s，而在光滑控制器的作用下，瞬态阶段被延长为0 s到7 s。无控制器作用下，负载最大残余扭转速度的实验值与仿真值分别为21.86°/s和22.88°/s，而在光滑器作用下负载最大残余扭转速度的实验值和仿真值分别为6.79°/s 和0.02°/s。从数据上分析来看，光滑控制器抑制了负载残余扭转速度的最大幅值，抑制比为：实验值68.94%，仿真值99.91%。

图4.8　负载扭转的实验响应

该驱动距离下，仿真的扭转速度也基本上被抑制为零，这也符合设计的光滑控制器对理论模型的抑制效果，即零残余振动抑制效果。同样，也是由于使用的光滑器的设计频率不是最匹配当前实验台，实验中有一些残余振动未被完全抑制住，导致抑制效果稍逊色一些，但也已经有很不错的抑制作用。同时在该驱动距离下，光滑器的抑制作用也降低了负载的扭转速度频率，从实验值的0.43 rad/s 抑制为0.10 rad/s，即负载扭转速度的变化周期也增长了，负载扭转运动的激烈程度也被削弱了。综合来看，在80°驱动距离下，光滑控制器不仅抑制了负载的扭转速度幅值，同时也降低了扭转速度的频率。

图4.9为不同驱动距离下，有无光滑控制器时负载残余摆动最大振幅对比图。横坐标代表回转电机的驱动距离范围，在0°～100°；纵坐标代表残余振幅值。使用未经过光滑整形处理的梯形指令驱动吊臂电机，当吊臂回转距离增加时，负载残余摆动的最大振幅出现交替的波峰和波谷变化。但是，经过光滑器作用后负载残余摆动的最大振幅变化却与吊臂回转运动距离无关，这是因为光滑器消除了负载的大部分残余摆动。通过光滑器作用下的仿真和实验结果对比可知，光滑器作用的实验结果略微差于仿真结果，这是由于仿真模型的建模差异和较小的不确定性造成的。(www.xing528.com)

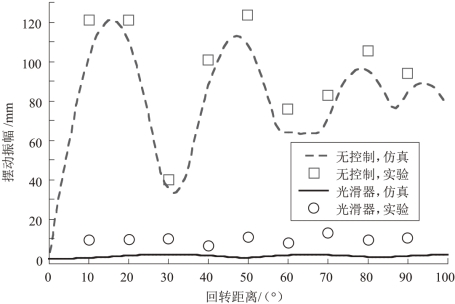
图4.9　回转距离对负载摆动的影响

图4.10展示了负载残余扭转速度的最大幅值和扭转频率的曲线结果。利用Matlab软件里的快速傅里叶变换对仿真数据和实验数据进行了扭转频率的计算，从而得到了不同驱动距离下的扭转速度频率。随着吊臂驱动距离的变化，负载的扭转速度幅值和扭转速度频率也会出现波峰和波谷。当摆动幅值达到最大值时，负载承受的扭转加速度也达到最大值，从而使负载的扭转角速度幅值和扭转频率均达到峰值。这种现象如前面对塔式起重机动力学模型进行分析预测的那样，增加摆动幅值会引起负载扭转速度幅值和频率的增加。在光滑器的作用下，残余扭转速度的实验值随着吊臂电机驱动距离的增加而增加，这是因为塔式起重机仿真模型是无阻尼的，而实验台系统是存在一些小的阻尼的。小的阻尼会破坏光滑器对吊臂电机长距离运动时负载的振动抑制效果。实验结果与仿真结果基本保持一致。光滑器使实验摆幅、扭转速度振幅和扭转速度频率分别平均降低了89.8%、71.7%和71.0%。实验结果验证了塔式起重机模型的动力学特性和光滑器对负载残余摆动和扭转运动抑制的有效性。

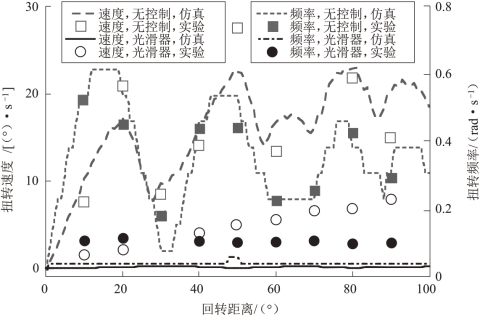
图4.10　回转距离对负载扭转的影响

光滑器在实际的使用中，需要对塔式起重机负载系统的结构参数值进行估算才能计算对应的控制器设计频率。由于工程测量估算肯定会存在偏差，而且设备在工作过程中各个参数可能会时刻改变，从而导致估算的设计频率与真实的频率存在偏差，即频率估计不准确。那么基于有偏差的设计频率设计的光滑器对于负载残余摆动和扭转运动是否还有足够满意的抑制效果呢，这就需要分析光滑器鲁棒性能的强弱了。鲁棒性是指控制器在一定的参数误差变化下，依然能维持其性能的特性。这种特性是控制器能否应用到工程实际的关键指标。

针对光滑器鲁棒性分析，设计了鲁棒性实验方案。选定吊臂电机80°驱动距离下，其余起重机结构参数和速度参数均不变条件下进行实验。光滑器理论计算的频率为ω1=4.032 rad·s-1，这个频率认为是模型的准确频率，设为基准频率。定义光滑控制器的设计频率为ω0。在实际工程应用中，对模型参数的估计计算不准确，这就会导致光滑器设计频率ω0不准确，会偏离系统的理论频率ω1。这样，鲁棒性实验便可以设计为：选定一个较合理的范围区间，人为更改设计频率ω0来设计对应的光滑控制器，通过实验来测试控制器的抑制效果。将设计频率ω0与理论频率ω1的比值定义为系统的归一化频率ω1/ω0，选择归一化频率区间为0.6～1.4，对应的设计频率ω0区间为2.419 rad/s到5.645 rad/s。选取归一化频率为0.6（2.419 rad/s）、0.8（3.226 rad/s）、1.0（4.032 rad/s）、1.2（4.838 rad/s）和1.4（5.645 rad/s）五个点进行鲁棒性实验。由于归一化频率为1.0 的光滑器实验已经做过，该部分只需要做其余四个点的实验即可。

图4.11 和图4.12 分别为80°驱动距离下不同归一化频率时负载的残余摆动和残余扭转速度的时域对比曲线。归一化频率为1 时，负载摆动和扭转的残余振幅分别为9.9 mm 和6.8°/s。而不受控制的响应摆动和扭转的残余振幅分别为105.7 mm 和21.9°/s。当归一化频率为0.8（对应于3.226 rad/s 的设计频率）时，摆动和扭转的残余振幅分别为11.1 mm 和8.0°/s。当归一化频率设定为1.2（对应于4.838 rad/s 的设计频率）时，摆动和扭转的残余振幅分别为18.6 mm 和8.3°/s。归一化频率0.6 的摆动和扭转的残余振幅分别为10.1 mm 和7.6°/s，而归一化频率1.4 的摆动和扭转的残余振幅分别为36.8 mm 和9.0°/s。鲁棒性实验结果表明，图4.11 中，增加光滑器设计频率的模型误差，控制器的负载摆动抑制效果会变差，负载的残余摆动量逐渐增加。由于光滑控制器具有低通滤波特性，归一化频率小于1 时载荷的残余摆动对建模误差并不敏感，负载的残余摆动被限制在一个很小的范围内。图4.12 表明，光滑器作用下，残余扭转速度响应对于设计频率的模型误差并不敏感，残余速度幅值和频率基本保持不变。总之，光滑器将负载的残余摆动和扭转均限制到较低水平，并且为频率中的模型误差提供了很强的鲁棒性。

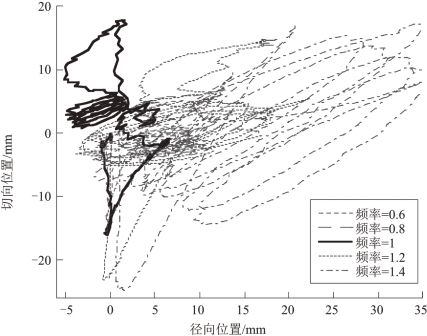
图4.11　频率模型误差对负载摆动的影响

图4.12　频率建模误差对负载扭转的影响

实验结果表明随着频率建模误差的增大，负载摆动逐渐增大。由于低通滤波特性，负载摆动在低频表现出不敏感性。实验结果显示被控扭转响应也对频率建模误差表现出不敏感性。光滑器抑制负载摆动和扭转到很低程度，对频率建模误差表现出很好不敏感性。