塔式起重机运载分布质量负载动力学模型，因其为双摆模型和负载为分布质量梁，且引入了起重机的回转运动，所以其动力学模型相当复杂。对该模型使用传统的拉格朗日方法，会很耗时耗力，且效率有限，因此使用分析力学的凯恩方法。
图4.2是分布质量负载塔式起重机动力学模型图。塔式起重机基座固定在地面上，横梁围绕基座的轴线旋转θ角度，牵引小车沿着吊臂方向作径向距离为r的滑动。一根长度为ls无质量的悬索吊挂在牵引小车的下方。悬索的另一端悬挂了一个质量为mh的吊钩。质量为mp、长度为lp的均匀分布质量的细长梁，通过两根长度均为lr的无质量吊索连接到吊钩上。
为了解释悬索摆动角αx 和αy、吊索的摆动角βx 和βy、负载的扭转角γ，该模型定义了牛顿坐标系Nxyz 和三个动坐标系Txyz、Cxyz 和Yxyz。牛顿坐标系Nxyz 如图4.2 所示，原点定义在吊臂与基座轴线的交点处。动坐标系Txyz 固定在小车上，坐标轴Tx 垂直于吊臂方向，坐标轴Ty 沿吊臂向外方向，坐标轴Tz 为竖直向下方向。动坐标系Cxyz 固定在吊绳上，坐标轴Cz正向沿吊绳向下。动坐标系Txyz 旋转摆动角αx 和摆动角αy 得到动坐标系Cxyz。动坐标系Cxyz 旋转摆动角βx、摆动角βy 和扭转角γ 得到另一动坐标系Yxyz。
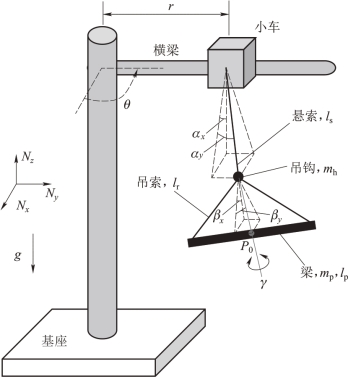
图4.2 塔式起重机运载分布质量梁物理模型
该模型假设塔式起重机负载系统的阻尼为零，如吊钩摩擦阻尼、空气阻尼等。由于塔式起重机横梁的传动是由高速比齿轮传动的，且传动电机由控制器按照预定速度曲线进行调速作用，所以可以假设负载的运动不影响起重机吊臂的运动，而且假设吊臂的回转电机带动吊臂运动平稳，即起重机在运动过程中不会产生机械结构振动，从而不会给负载的运动带来额外干扰。吊钩体积相对分布质量梁的尺寸较小，可以简化为质点处理，即吊钩只有点质量。吊绳被假设为无质量，且不会发生弯曲变形、扭转变形和长度变化。实验时，吊绳使用的是大力马钓鱼线，该线的特点是绳子的扭转刚度很小，且由于重力的作用，负载摆动的角度不会超过45°，即吊绳一直处于拉伸状态，不会发生弯曲变形，负载不会出现因失去吊绳的束缚而发生突然冲击现象，损耗系统的机械能。两根吊索也被假设为无质量，且在运动过程中不发生变形。分布质量负载细长梁被简化为质量沿其轴线均匀分布、只有长度、没有截面尺寸的刚体，也就是说负载在运动过程中，不考虑其绕轴线自转的运动。
塔式起重机动力学模型的输入是吊臂的角加速度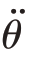
以及小车的加速度
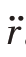。模型的输出是悬索摆动角αx和αy，吊索摆动角βx和βy，以及负载的扭转角度γ。使用凯恩方法，导出了图4.2中模型的非线性动力学方程：
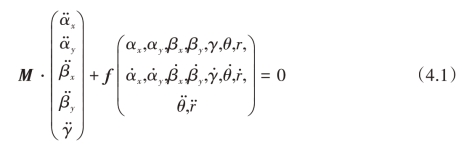(www.xing528.com)
式中，M代表质量矩阵；f是包含有重力、离心力、科氏力以及系统控制输入项在内的列矩阵。
图4.3 为起重机横梁电机驱动距离为80°时负载质心摆动的轨迹图，为俯视角度下的轨迹图。横坐标和纵坐标分别代表负载质心的径向位置（即沿着吊臂方向）和切向位置（即垂直吊臂方向）。图中坐标原点代表负载质心的静止平衡点。图中折线段轨迹为横梁电机驱动时负载质心的瞬态摆动轨迹，而椭圆段轨迹为电机停止后负载质心的残余摆动轨迹。吊臂从0 s 按照梯形速度曲线以67°/s2加速度开始加速，这引起了负载的摆动和扭转。然后，吊臂开始以20°/s 的速度匀速运动，吊臂在4 s 后以67°/s2减速度开始减速，这会引起负载额外的振荡。因为切向方向为塔臂的旋转方向，所以负载质心的切向振幅要大于负载的径向振幅。图中，负载质心最大残余摆动量的实验值为105.66 mm，仿真值为95.27 mm。从图中可以看出，负载在瞬态运动过程中，实验轨迹图与仿真轨迹图基本重合，实验数值略微大于仿真值。在残余运动过程中，同样实验数据比仿真数据稍微大一些。实验数据大于仿真数据，是由于实际电机速度曲线与设计的仿真速度曲线存在差异，而且仿真程序里测量的起重机参数与实际数值之间存在误差。总体而言，在80°驱动角度下，实验和仿真的质心摆动轨迹图有相当好的一致性。
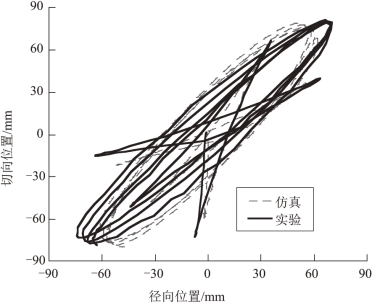
图4.3 负载摆动实验验证
图4.4 为驱动距离为80°时负载扭转速度图。图中的横坐标代表时间，纵坐标代表负载的扭转速度。0～4 s 段为电机驱动时间段，此时负载的扭转属于瞬态扭转阶段，该过程电机带动吊臂经过了加速—匀速—减速三个阶段。4 s 以后为电机停止运动后负载的残余扭转阶段。从0 s 开始，在回转电机加速运动过程中，负载扭转速度开始负向加速，速度很快达到20°/s，之后开始接近匀速运动，这个阶段速度曲线会出现高频振动现象。4 s 左右，回转电机开始减速到静止，负载扭转速度开始反向加速，然后开始以零速度作为平衡位置作周期振动。该阶段负载的残余扭转速度曲线近似为正弦曲线。在残余运动阶段，扭转速度最大幅值：实验值为21.86°/s，仿真值为22.88°/s，实验值略小于仿真值。由于摩擦和空气阻力的影响，实验曲线的幅值在逐渐衰减，仿真幅值由于未考虑这些因素，速度幅值没有变化。通过对图4.4 中扭转速度曲线的速度幅值和振动周期的吻合程度进行分析，可以得出，在80°驱动角度下，实验数据能很好地匹配仿真数据。根据对图4.3和图4.4两图的分析比对，可以得出在该距离下实验能很好地验证仿真模型的正确性。
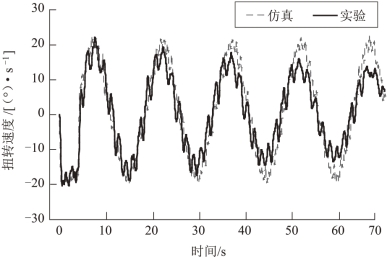
图4.4 负载扭转实验验证
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
