动力学模型的建立与分析

图3.24 给出了在风扰动下带分布质量负载的桥式起重机示意图。其中，小车在轨道上以加速度a沿着x方向运动。可将长度为lh且质量忽略不计的第一级悬索，一端挂在小车上，另一端通过长度为lv质量忽略不计的第二级吊索与质量为mp、长度为lp的均匀分布质量梁负载相连。持续风力wf沿着x方向垂直作用于负载上。

图3.24　风扰动下带分布质量负载的桥式起重机

由于外界风扰动的方向对分布质量负载的扭转有很大影响，一旦负载发生扭转，图示起重机的动力学模型会变得非常复杂。因此，在设定分布质量梁负载的方向与风力及轨道垂直后，就不会引起梁负载的扭转，该假定在一定程度上对系统动力学模型进行了简化处理。

图3.24所示的带分布质量负载的桥式起重机系统，其输入量为：小车加速度a，第一级悬索长度lh和风力wf；输出量为第一级吊索的摆角θ。由于驱动系统存在非常大的机械阻力，模型中假定分布质量梁负载的运动不会对小车的运动产生影响，同时也假设该柔性机械系统的振动阻尼为零。利用凯恩方法，可以得出图示物理模型的运动方程，即摆角与小车加速度、第一级悬索长度，以及风力之间的非线性运动方程：

其中，g为重力加速度常量。假设分布质量梁负载为小角度摆动，可以得出该系统的线性化频率：

(www.xing528.com)

从系统频率公式（3.21）可以看出，影响系统频率的参数有第一级悬索长度、第二级吊索长度以及分布质量梁负载的长度。通常情况下，第一级悬索长度的变化是影响系统频率的主要因素，同时，负载长度的改变对系统频率的变化也有很大的影响。

通常，可以将用来驱动吊车系统运动，并完成预定任务的原始操作员命令看作是一个梯形速度命令。当操作员按下操作手柄上面的启动按钮时，该梯形速度命令开始出现，并且随着时间的推移而变大，直到驱动系统达到最大速度；然后，驱动系统以该最大速度运行，直到操作员松开手柄上面的启动按钮；随后，该速度命令开始下降，一直下降到零为止。

图3.25 给出了桥式起重机模型在无控制时的模拟负载振荡曲线。其中，预定任务为驱动吊车运动1.4 m，外部连续风扰动为0.2 N。第一级悬索长度、第二级吊索长度、负载长度和质量分别设定为1.0 m、0.5 m、0.5 m 和0.3 kg。外部风扰动从0 s时刻开始作用于系统，并迫使负载产生一个振荡。吊车的驱动机构在4.5 s时刻开始，以加速度2 m/s2、最大速度0.2 m/s启动，这个启动过程又会使负载产生一个新的振荡。紧接着，驱动机构的减速过程又会引发系统产生额外的振荡。

整个系统响应过程可以分为三个阶段，初始阶段、瞬态阶段和残余阶段。其中，初始阶段定义为，从零时刻到系统的驱动机构启动之前这段时间。在该阶段，负载在外界的连续风力作用下产生稳定的振动，初始阶段的振动峰-峰值被定义为初始振幅。瞬态阶段定义为，驱动机构处于运动的这段时间，瞬态阶段的负载振动峰-峰值被定义为瞬态振幅。残余阶段定义为，驱动机构停止运动后的这段时间，残余阶段的负载振动峰-峰值被定义为残余振幅。

如图3.25所示，在外界风扰动及原始操作员驱动命令的共同作用下，吊车负载产生的瞬态振幅和残余振幅分别为31.5 cm和16.4 cm。在上述仿真条件下，由于驱动器的加速过程引起的桥式吊车负载振动与外界风扰动引起的负载振动相位相同，因此，瞬态振幅与初始振幅相比有明显的增大。此外，由于驱动器的减速过程引起的负载振动与瞬态振动相位相反，因此残余阶段的振幅与瞬态振幅相比又有显著的减小。仿真结果清楚地展现出，带分布质量负载的桥式起重机在连续风扰动下的动力学模型变得更加复杂；同时，在系统经受连续外扰动的作用时，负载振动的平衡位置发生了改变，驱动起重机完成预定任务对操作员来说也更加具有挑战性。因此，对连续风扰动下带分布质量负载的桥式起重机的动力学特性进行分析，并提出一种有效的控制方案，以消除由外界连续扰动以及操作员命令引起的系统振动，有着迫切的需要。

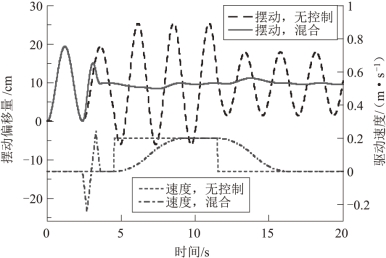
图3.25　小车运动和风扰动作用下振荡响应