设计过程中的频率和阻尼比误差为零的解决方法及其局部极值控制

高阶模态在某些情况下对机械系统的动力学也有一定的影响。因此激励起的高模振动也需要被抑制。为了实现光滑器的低通滤波特性，在两倍设计频率处的振幅也应该被限制为零：

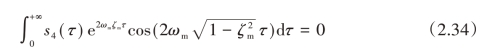
式中，ωm是固有频率的设计值；ζm是对应的阻尼比设计值。

当频率和阻尼比建模误差为零时，通过约束方程（2.33）和方程（2.34）可以将两倍频率处的振动也抑制为零。然而，实际工况在高阶模态具有某种程度上的不确定性因素。因此，需要添加其他的约束来加强高模频率的鲁棒性。在两倍频率处，振幅对频率的导数也要被限制为零：

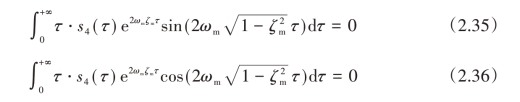
为了使设计频率附近的鲁棒性达到最大化，还需要限制两个频率修正点p·ωm和r·ωm处的振幅为零。设计频率位于两个修正频率中间。对两个频率修正点处的零振动约束可以表示为：

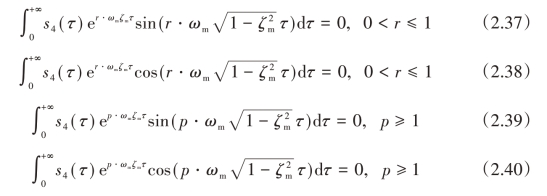
为了使光滑后的指令和原始指令有相同位移，光滑器应该具有单位增益约束。通过单位增益约束和约束方程（2.33）～方程（2.40），然后基于时间最优求解出四段光滑器［25］：

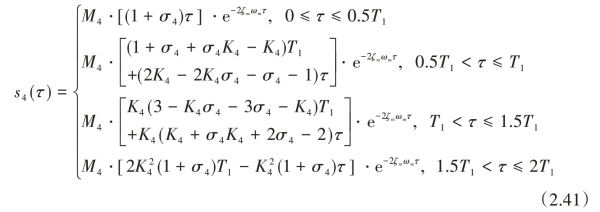
式中，σ4是系数。系数K4和M4的表达式如下：(www.xing528.com)

四段光滑器的轮廓曲线如图2.10所示。它是一个分段连续函数，具有四个分段，每个分段都在边界处具有连续特性。因此被称为四段光滑器。四段光滑器的传递函数表达式为：

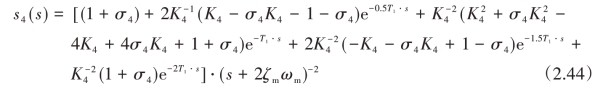
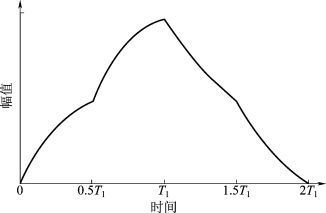
图2.10　四段光滑器

由频率设计点约束和两个频率修正点约束可知，在频率设计点附近，百分比残余振幅存在一个局部极值。假设这个极值处的频率为v·ωm，其中r≤v≤p。这个局部极值需要被限制到容许振幅：

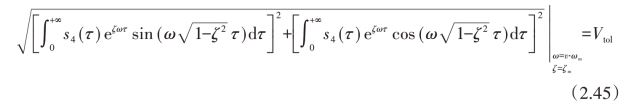
容许振幅Vtol由实际系统的设计要求来确定。由于是局部极值点，所以在该点处还具有零斜率约束：

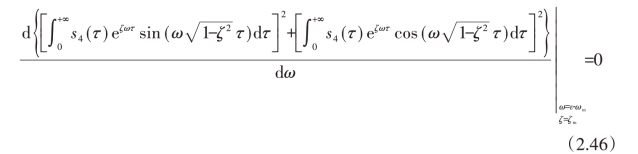
四段光滑器方程（2.41）中的系数σ4能够通过式（2.45）和式（2.46）求解。但是由于方程组的非线性，封闭解析解很难得到。将四段光滑器方程（2.41）带入式（2.45）和式（2.46），可以求解出数值解。当容许范围Vtol被设置为零时，系数σ4的数值解也为零。