基础激振与振动台试验及瞬态响应分析

基础激振又称为加速度加振，是指因为结构物的约束部位（支承部位）的加速度不为零的运动而引起的结构物自身的振动。如果加速度为零，由于约束部位处于静止或匀速运动状态，不会引起结构物自身的振动。这样的基础激振，在试验室里可看作将结构物固定在振动台上进行试验，即振动台试验（见图1-193）。

图1-193 基础激振和振动台试验

a）振动台 b）加速度传感器

实际的结构物固定在振动台上后，要用加速度传感器来测量其动态响应。

下面将利用一个案例来说明如何在时间域里进行动态响应分析。

案例：挂架的瞬态响应分析

瞬态响应分析是在时间域的响应分析。

一个完整的瞬态响应分析有以下几个步骤：静应力分析：求解结构物在有外载作用下的应力。该外载在接下来的响应分析中会被赋予随时间变化的特征；固有振动分析：求解用于模态叠加法用的固有模态；瞬态响应分析：定义外载随时间变化的特征（激励波的波形）和阻尼系数。求解的时间范围等条件确定后，进行求解和后处理。

（1）静应力分析　直接利用前面已定义的分析文档。

（2）固有振动分析　与上面调和响应分析一样，采用计算到60阶模态的固有振动模态作为模态叠加法的基，直接利用前面已定义的分析文档。

（3）瞬态响应分析 从下拉列表（见图1-194）中插入一个瞬态响应分析（Transient Dynamic Response Case）的案例，并在弹出的窗口中选择上述固有振动解作为模态叠加的基。注意选择基础激励（Restraint Excitation）。

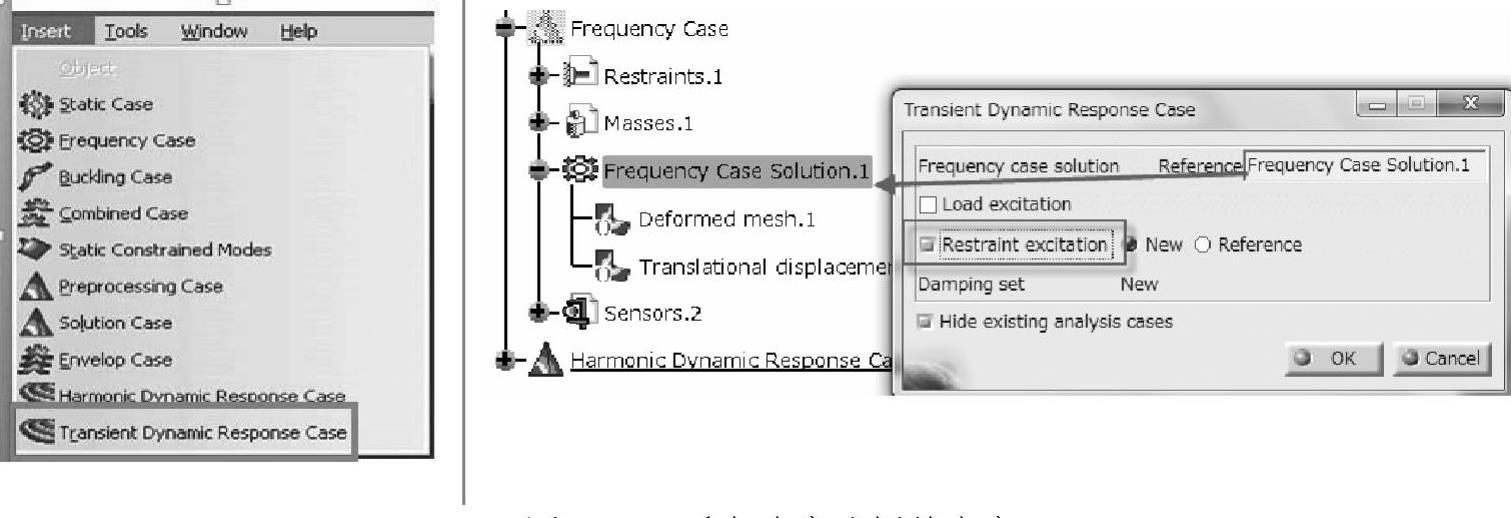
图1-194 瞬态响应分析的定义

此时特征树上自动生成瞬态响应分析的特征（见图1-195）。

定义外载随时间变化的特征（激励波的波形），可考虑振动台试验，在此预先用Excel定义了一个正弦变化的激励波的波形（见图1-196）。

图1-195 瞬态响应分析的特征

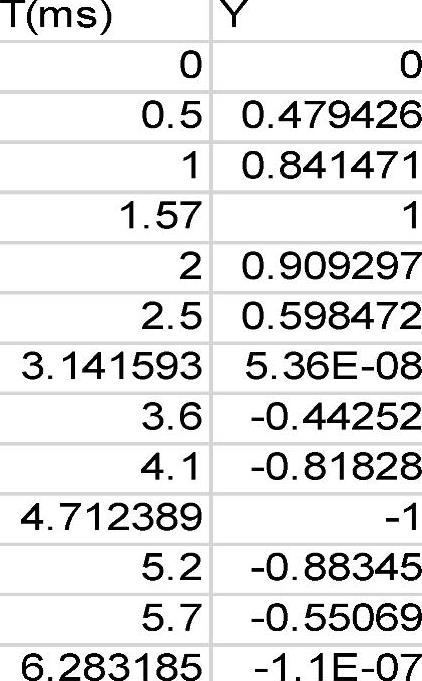
图1-196 用EXCEL定义一个激励波的波形

单击时间调制（Time Modulation）图标，选择已定义好的正弦变化波形的Excel文件，并在特征树上确认时间调制波形的节点（见图1-197）。

图1-197 定义激励波的波形

在此节点上单击右键，从下拉列表中选择生成二维图形（Generate 2D Dis-play），可以表示其正弦波形（见图1-198）。

图1-198 激励波的正弦波形

下一步是将此时间调制波的波形和基础运动相关联。如图1-199所示，双击特征树上的基础激励（Reastraint Excitataion.1）节点，并从特征树上选择时间调制波的特征，并在z方向给定一个重力加速度的值9.8m／s²来完成定义。其物理意义是物体（挂架）的约束部位在z方向有一个加速度大小为9.8m／s²、以正弦波形式变化的运动，这个基础运动导致了挂架的振动。目的是测试这个在6.28ms内的加速度加振会有什么样的动态响应。

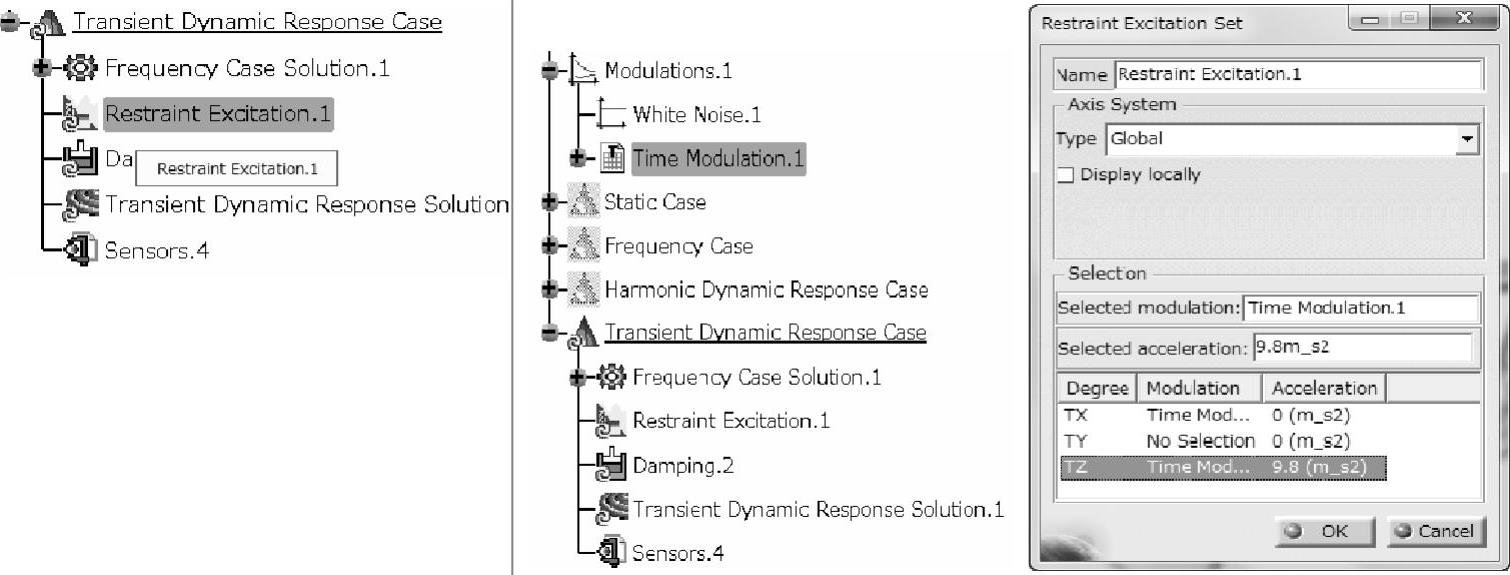
图1-199 基础激励的定义

定义了基础激励后，用调和响应的方法定义阻尼系数。同样，选择模态阻尼，并给出全模态的阻尼系数为临界阻尼系数的4％。

上述定义结束后，再来定义所需求解的时间范围。如图1-200所示，双击特征树上的瞬态响应分析解（Transient Dynamic Response Solution.1），在弹出的窗口中输入0～0.25s的时间范围，并分500等份来求解。(www.xing528.com)

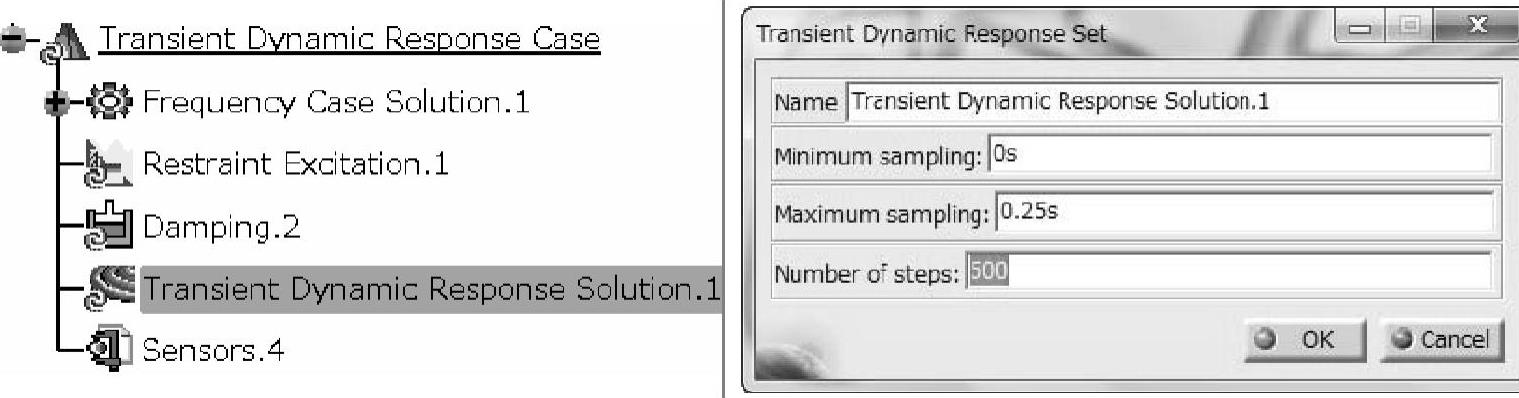
图1-200 瞬态响应分析求解范围的定义

计算完成后，可进行后处理。如图1-201所示，在特征树的瞬态响应分析解（Transient Dynamic Response Solution.1）上单击右键，选择生成二维图形（Gener-ate 2D Display），并在相对坐标系中表示二维图形。选择所需表示动态响应的节点表示二维图形。

基础激励常表示的是相对坐标系中的结果，即人站在振动台上观察动态响应，以便排除基础运动的影响，直接得到结构物的响应。

图1-201 瞬态响应分析的后处理

默认表示的是该节点的变形振幅-时间的图。可以在纵轴上选择dB表示变形量分贝-时间的图（见图1-202）。

除上面的表示外，还可输出实际变形量与时间和相位角与时间的图（见图1-203）。

除了表示变形量和时间的关系外，有时需知道速度、加速度与时间的关系。如图1-204所示，做法是在上面的二维表示的纵轴的空白处单击右键，从下拉列表中选择Select Data，再在弹出的窗口中选择速度、加速度，即可显示速度、加速度对时间的二维表示。

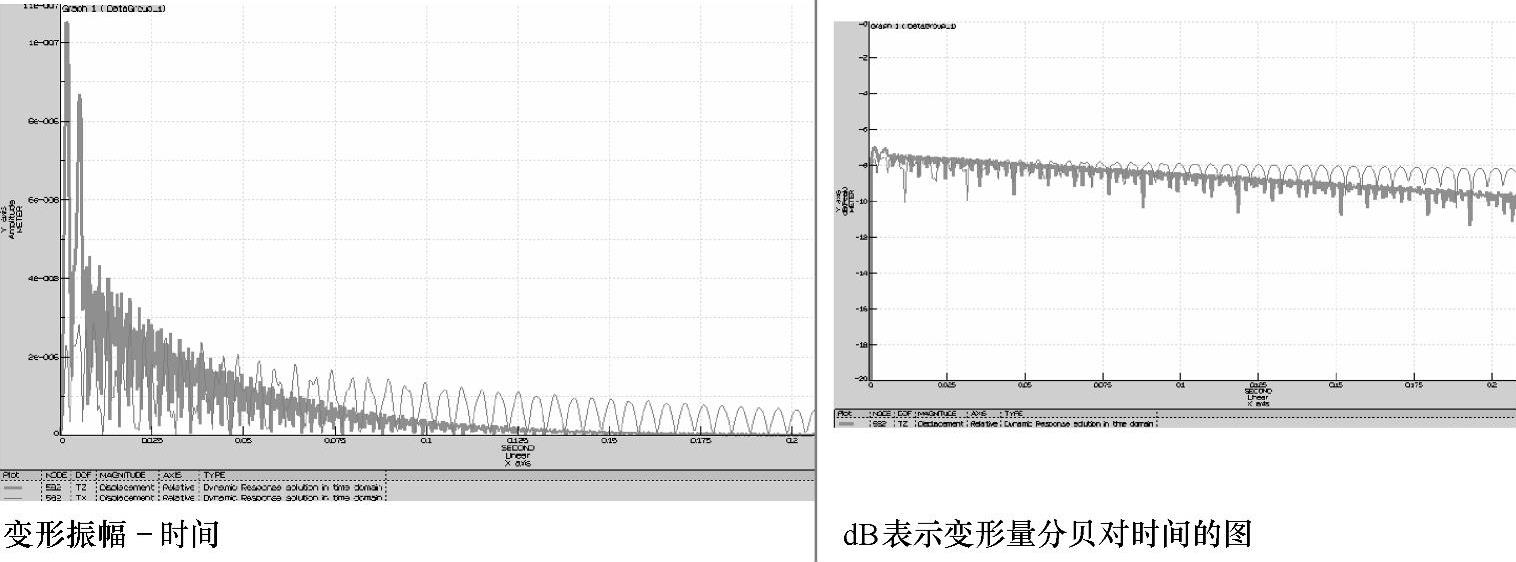
图1-202 瞬态响应分析的后处理

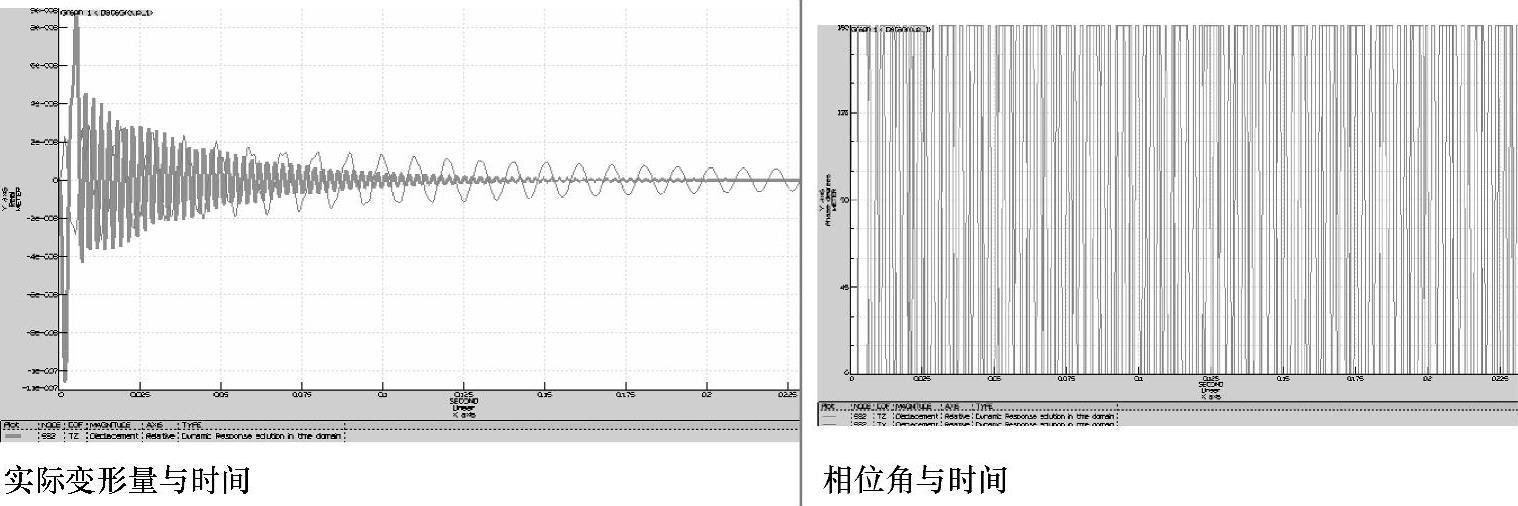
图1-203 瞬态响应分析的后处理

二维图除可表示某一节点的动态响应外，还可以表示某一时刻全结构的位移和应力分布。下面表示的是3ms时位移和应力值以及分布图（见图1-205）。

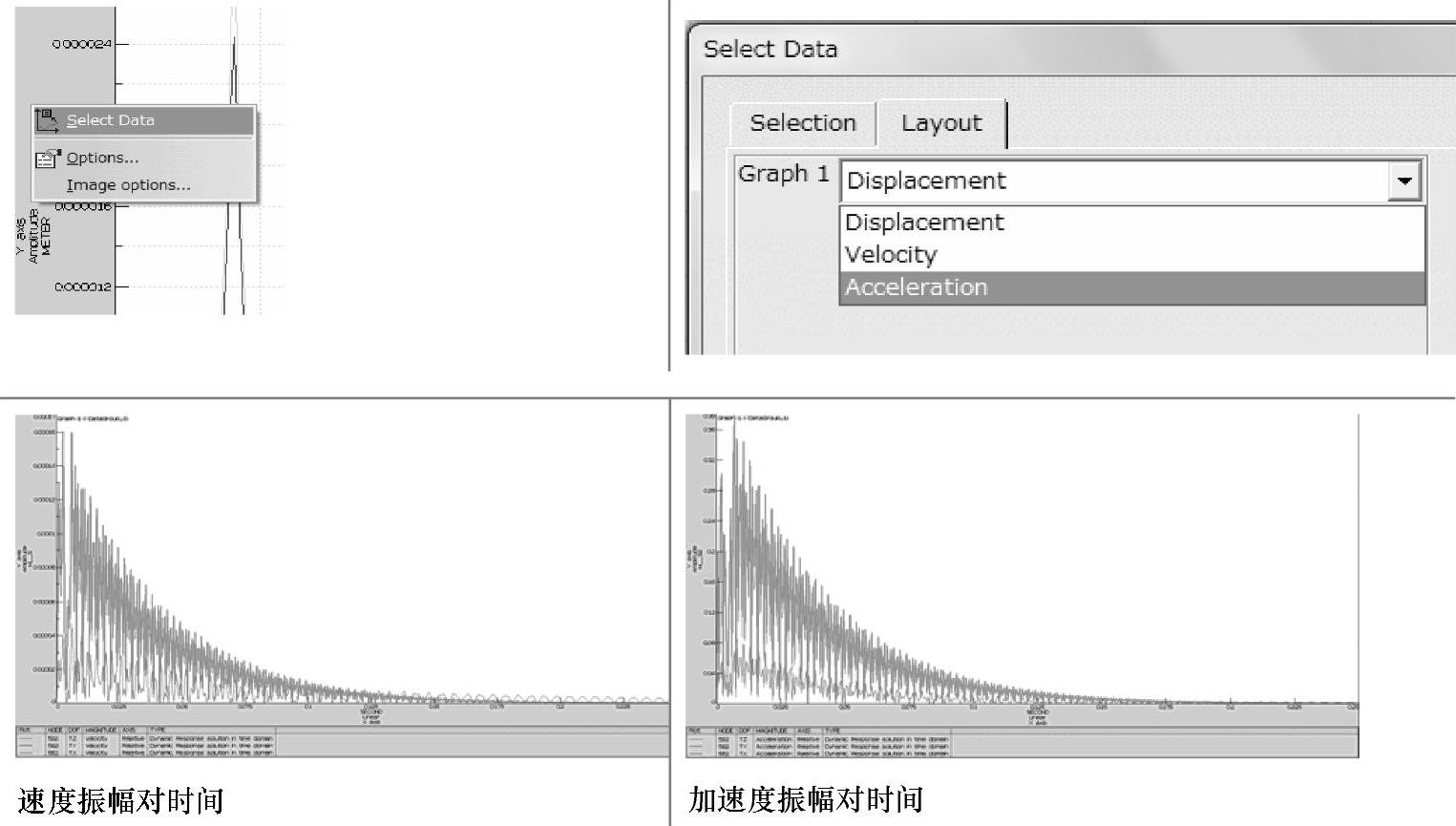
图1-204 瞬态响应分析的后处理

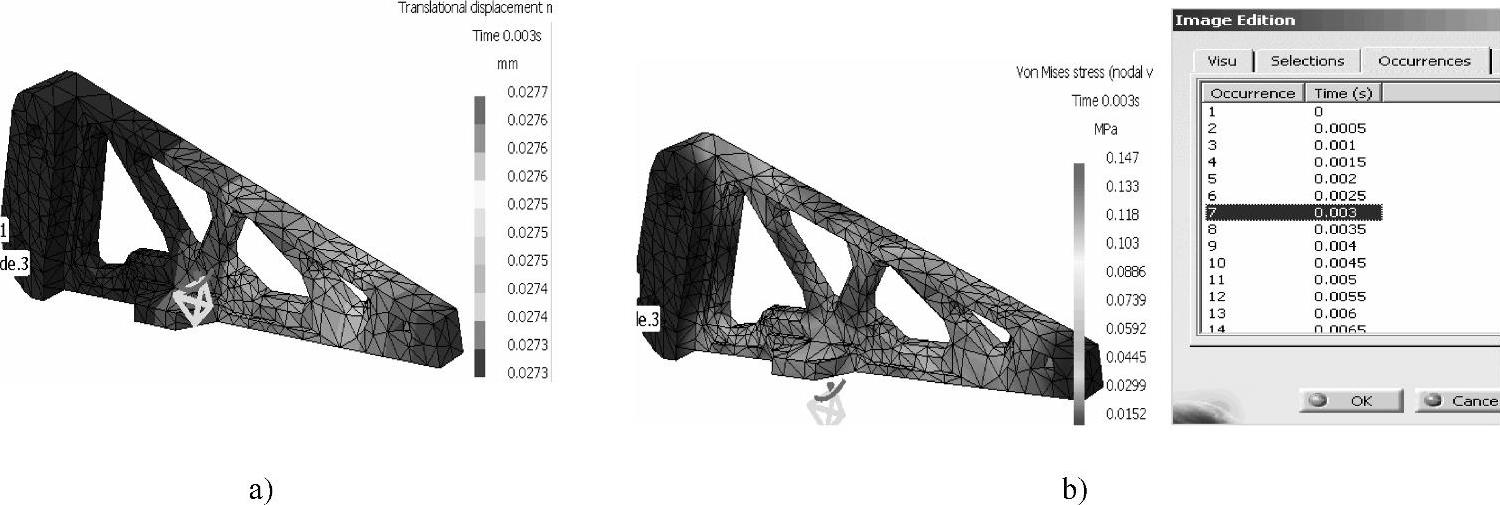
图1-205 瞬态响应分析的后处理

a）3ms时的位移 b）3ms时的等效应力

表示了位移或应力后，可对整个分析的时间范围进行动画表示。动画表示分绝对坐标系和相对坐标系中结果的两种表示方式，可方便、清楚地观察基础激励的响应。其方法如图1-206所示，双击上述位移或应力的图像，在弹出的窗口中的Visu选项中，单击变形模式右边的按钮，再在新弹出的材料的窗口中选绝对坐标系和相对坐标系。

另外，也可显示相对坐标系中的位移、速度和加速度矢量。其做法如图1-207所示，在特征树的瞬态响应分析解（Transient Dynamic Response Solution.1）上单击右键，选择生成图像（Generate Image），选择所需表示动态响应的相对坐标系中的位移、速度和加速度矢量。

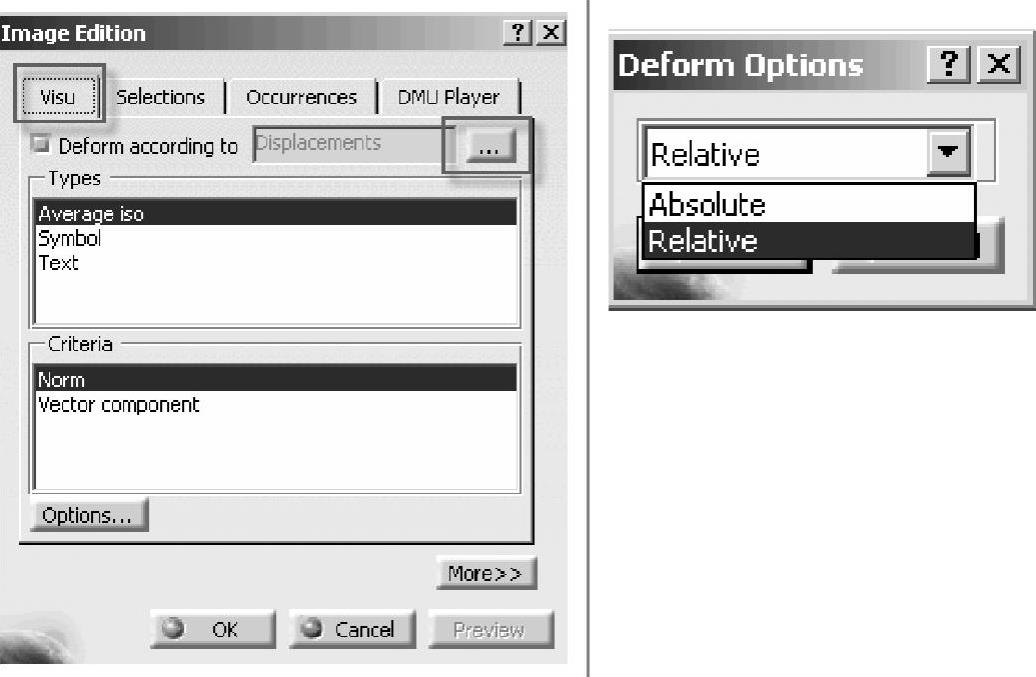
图1-206 绝对坐标系和相对坐标系中结果的表示方式

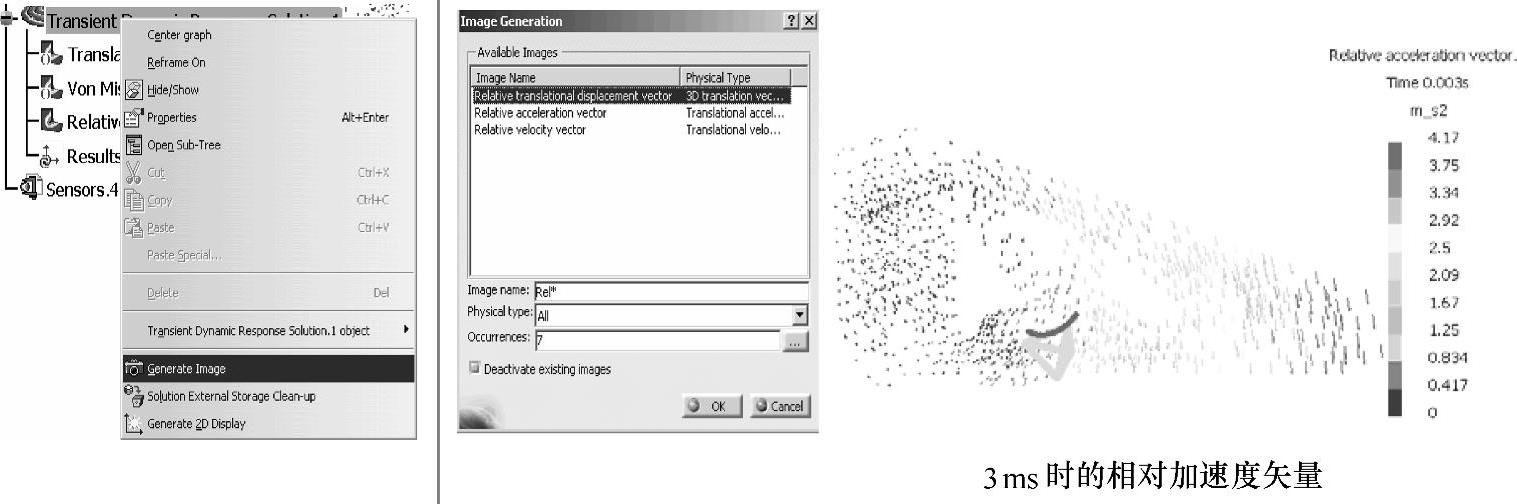
图1-207 显示相对坐标系中的位移、速度和加速度矢量

本案例主要是对应试验室里的振动台试验而设定的基础激励的瞬态响应分析。瞬态响应分析也可以是力激励（见图1-208）。在此不作详细表述，读者可自己练习体会。

图1-208 力激励的瞬态响应分析

本节着重讲述了在实际试制样品进行试验前，如何在产品的设计阶段来实施振动试验，以测试动态响应的水平来改进设计，提高产品质量。