力激振与锤击试验及调和响应分析析

力激振是指由随时间变化的外力引起的振动。在试验室中，常用的一个振动测试为锤击试验，即用锤子击打物体，将其产生的振动信号记录下来，用于测试的方法如图1-175所示。

锤击试验的一个特点是它激励了所有的固有模态。在频率域里，激励信号表现

图1-175 锤击试验

a）锤击试验 b）轮毂的锤击试验

为一条水平线（见图1-176），其信号有一个特别名字，称为白噪声（White Noise）。

图1-176 白噪声（White Noise）

下面将用一个案例来说明如何在频率域里进行表现锤击试验的动态响应分析。

案例为挂架的调和响应分析。

调和响应分析是在频率域的响应分析。

一个完整的调和响应分析有以下几个步骤：静应力分析：求解结构物在有外载作用下的应力。这个外载在响应分析中会赋予随时间变化的特征；固有振动分析：求解用于模态叠加法用的固有模态；调和响应分析：定义外载随频率变化的特征（激励波的波形）和阻尼系数。求解的频率范围等条件确定后，进行求解和后处理。

（1）静应力分析　直接利用前面已定义的分析文档。

与1.4节一样，定义挂架的约束和载荷条件如图1-177所示。

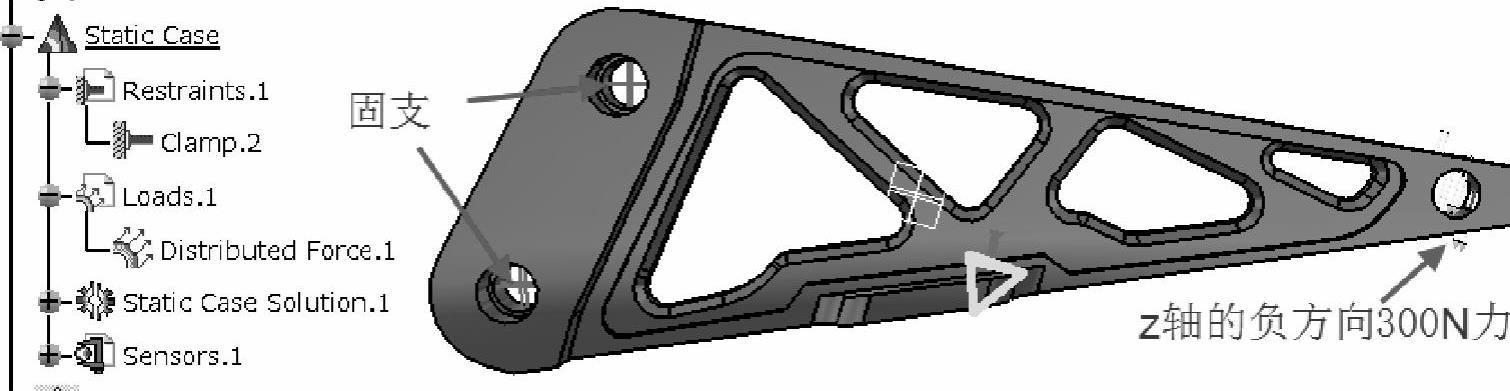
图1-177 挂架的约束和载荷条件

（2）固有振动分析 利用与静应力分析相同的约束条件进行固有振动分析。要注意应计算的固有模态的阶次。默认的计算阶次是10阶。用本篇第5章讲述的表示模态参与因子（Mode Participation Factor）的方法来确认所计算的固有模态的阶次是否足够。

在默认的情况下，计算10阶模态。在x、y、z的并行方向上的总的参与因子分别是81.19％、77.51％和81.09％。一般而言，总的参与因子要在90％以上为好（见图1-178）。

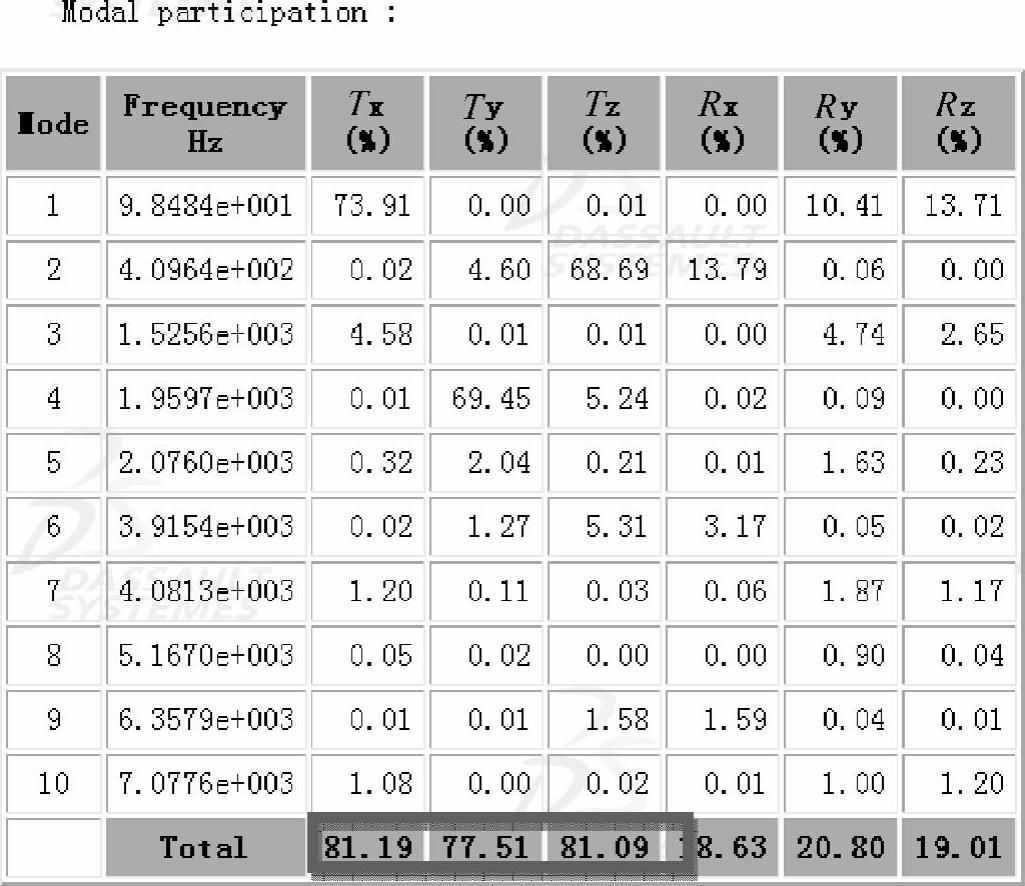
图1-178 模态参与因子

为什么必须计算足够的固有模态的阶次？从线性代数中的矩阵理论来看，固有频率和固有模态即特征值和特征向量。模态叠加法是在用特征向量作为坐标（又称为基）的N维空间（N＝特征向量的个数）中将其展开进行求解的方法。如果模态的阶数，即特征向量的个数不够，那么展开用的坐标就不完备，展开的结果（模态叠加法的结果）不能保证精确。换句话说，如果用5阶的模态来作响应分析与用15阶的模态来作响应分析的结果可能会不同。所以，正确的做法是用总的模态参与因子在90％（经验值）以上的模态阶数来作动态响应分析。

把所要计算的模态阶数从10改为60（见图1-179）。

图1-179 修改要计算的模态阶数（从10改成60）

重新计算后，从计算报告中可发现在x、y、z的并行方向上的总的参与因子分别为91.64％、90.40％和92.68％（见图1-180），可保证模态叠加法的结果有足够的精度。

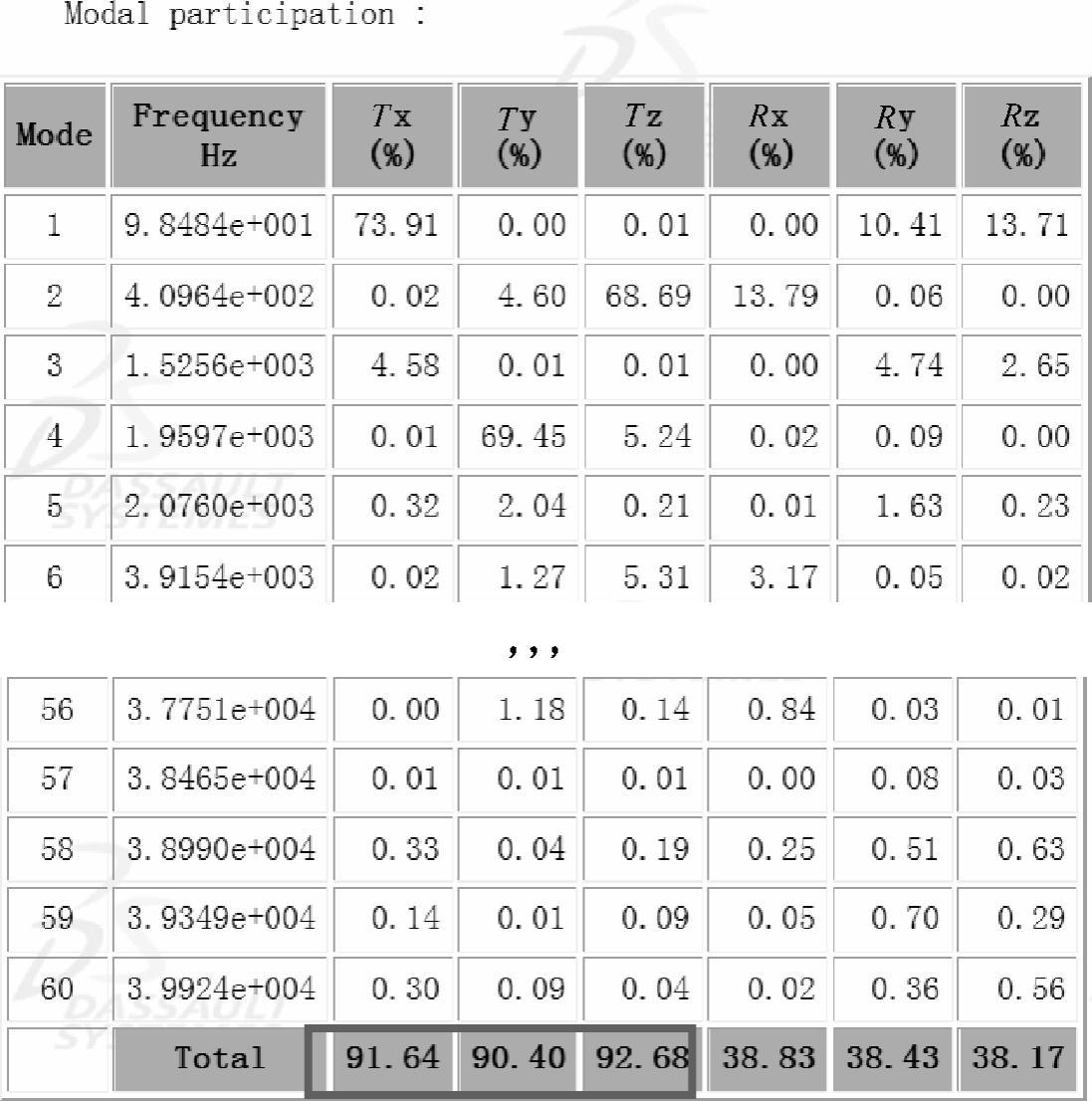
图1-180 模态参与因子

（3）调和响应分析　从下拉列表中插入一个调和响应分析（Harmonic Dynamic Response Case）的案例，并在弹出的窗口（见图1-181）中选择上述固有振动解作为模态叠加的基。

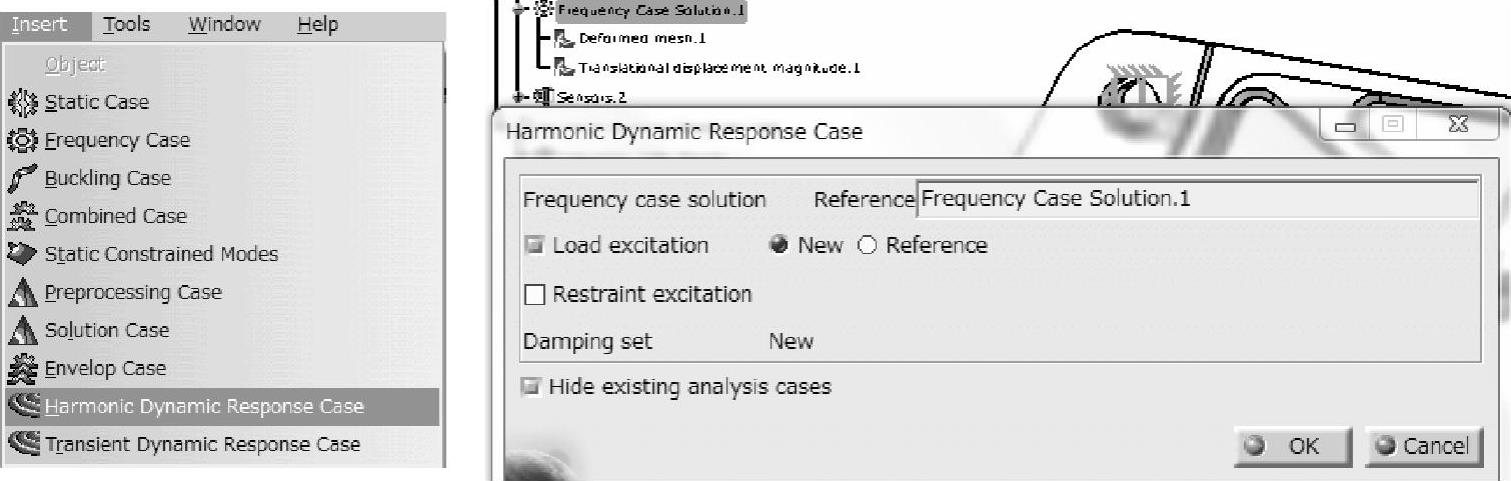
图1-181 调和响应分析的定义

此时特征树上自动生成调和响应分析的特征（见图1-182）。

定义外载随频率变化的特征（激励波的波形），可考虑锤击试验，此处选择白噪声（见图1-183）。

图1-182 特征树上自动生成调和响应分析的特征(www.xing528.com)

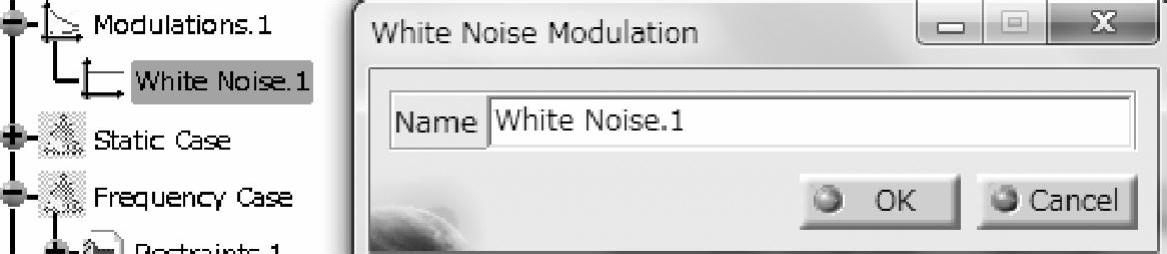
图1-183 定义外载随频率变化的特征（激励波的波形）

下一步是将白噪声激励波的波形和外力相关联。如图1-184所示，双击特征树上的载荷激励（Load Excitataion.1）节点，并从特征树上选择静应力分析中的载荷（－z方向300N）和白噪声的特征来完成定义。其物理意义是用300N的力在挂架前端的孔上锤击挂架，测试其动态响应。

图1-184 载荷激励的定义

定义载荷激励后，再来定义阻尼系数。阻尼衰减振动的机制较复杂。一般认为，阻尼是因振动引起了结构内部分子的运动，产生摩擦热而消耗了能量所致。如图1-185所示，双击特征树上的阻尼（Damping.1）节点，选择模态阻尼（也可以选择瑞利阻尼），并给定全模态的阻尼系数为临界阻尼系数的4％（一般金属结构的阻尼系数为临界阻尼系数的4％）。

上述定义结束后，再来定义所需求解的频率范围。如图1-186所示，双击特征树上的动态调和响应解（Harmonic Dynamic Response Solution.1），在弹出的窗口中输入0～5000Hz的频率范围，并分500等份进行求解。

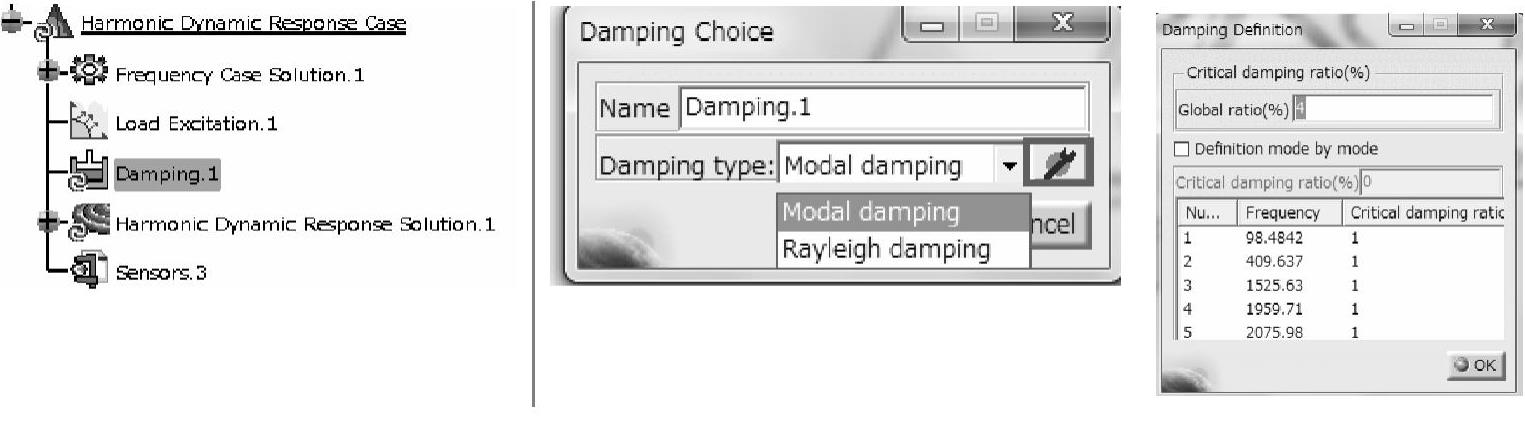
图1-185 定义阻尼系数

图1-186 定义所需求解的频率范围

模态叠加法的计算求解速度很快，计算完成后，可进行后处理。如图1-187所示，在特征树上的动态调和响应解（Harmonic Dynamic Response Solution.1）选项单击右键，选择生成二维图形（Generate 2D Display），并在绝对坐标系中表示二维图形。选择所需表示动态响应的节点表示二维图形。

图1-187 动态调和响应的后处理

默认表示的是该节点的变形振幅对频率的图，可以在纵轴上选择dB表示变形量分贝对频率的图（见图1-188）。

要注意的是，dB（分贝）是一个相对量。0分贝是指变形量在1μm时的值，建议在变形二维图的曲线上单击右键输出到Excel里计算画图。

除上面的表示外，还可输出实际变形量-频率、相位角-频率的图（见图1-189）。

除表示变形量和频率的关系外，有时需知道速度、加速度与频率的关系。如图

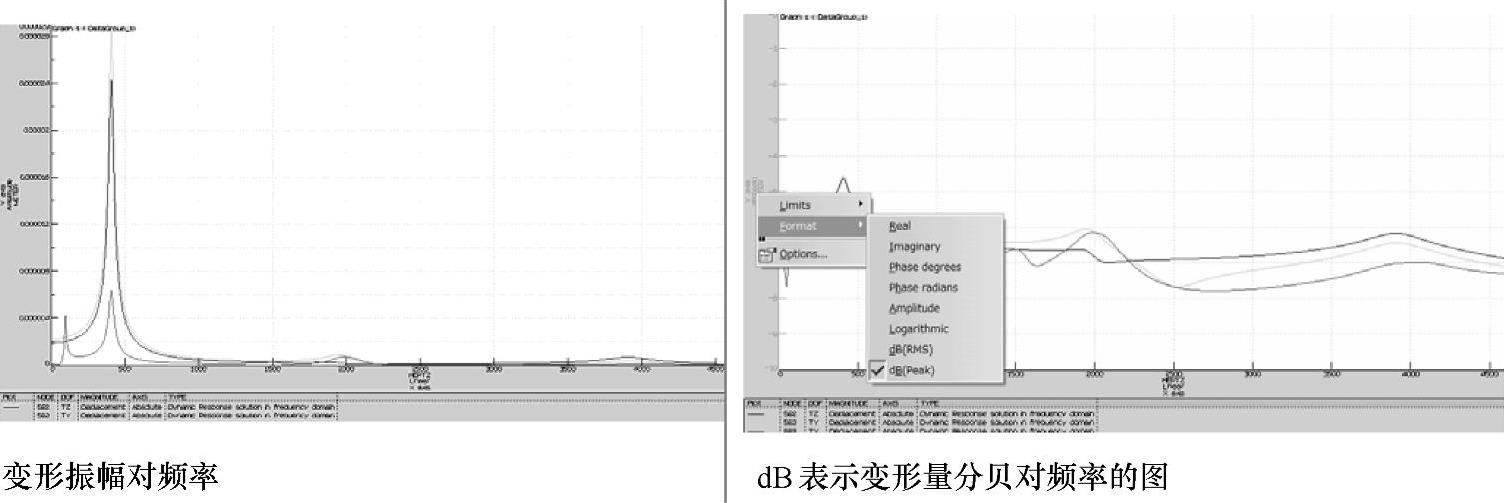
图1-188 动态调和响应的后处理

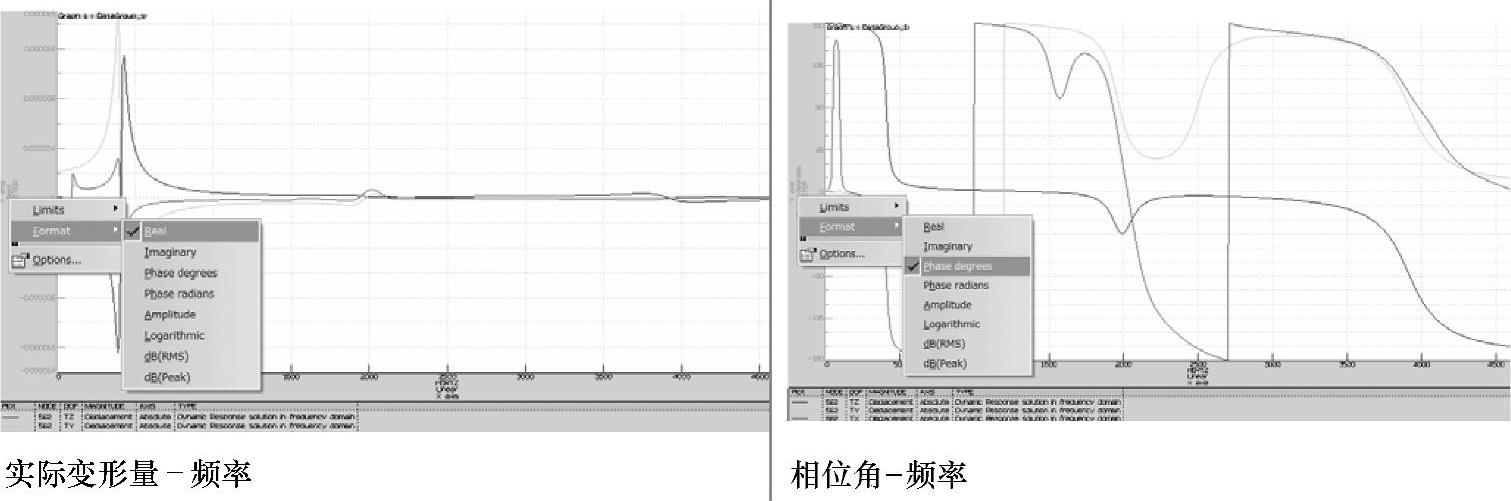
图1-189 动态调和响应的后处理

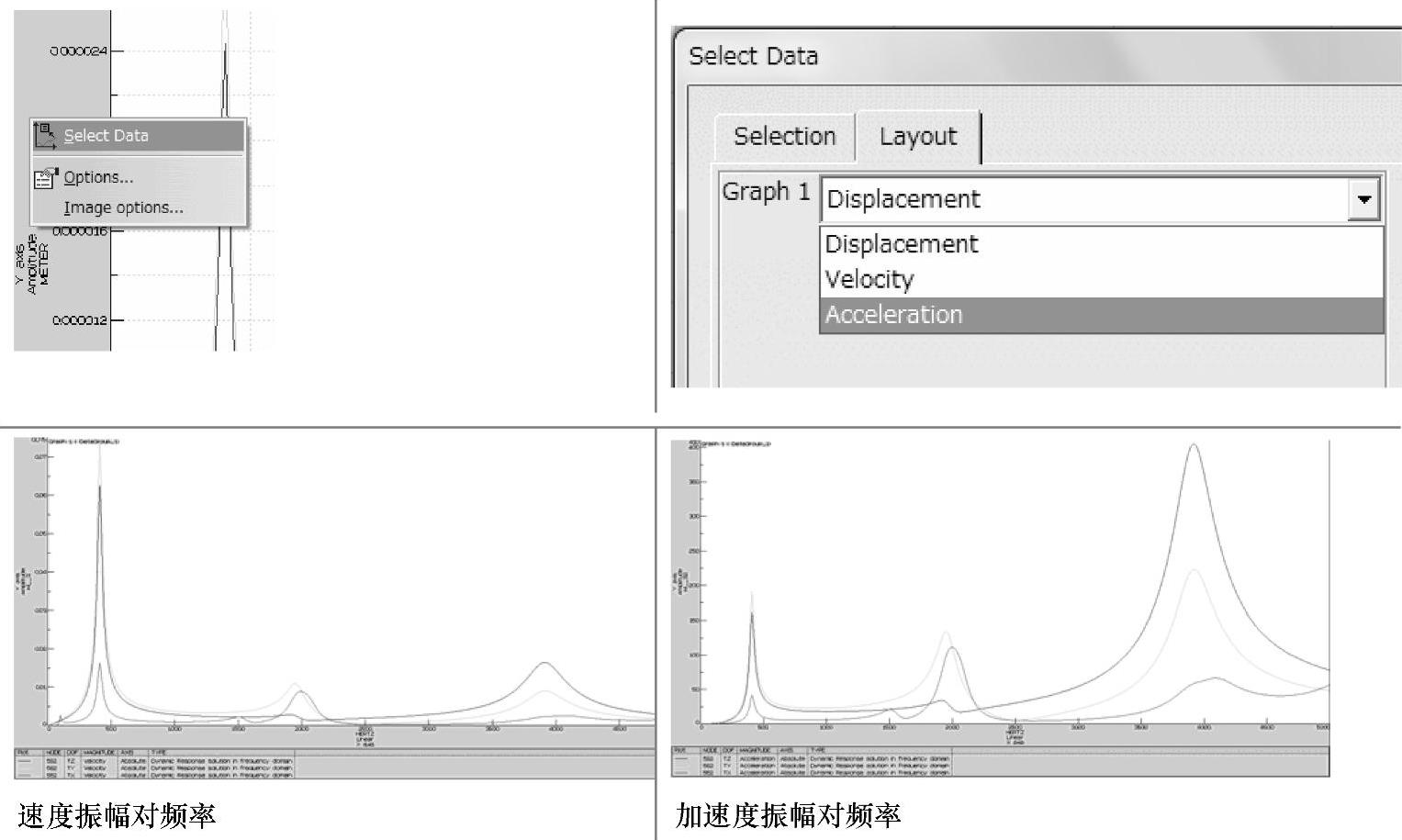
图1-190 动态调和响应的后处理

1-190所示，做法是在上面的二维表示纵轴的空白处单击右键，从下拉列表中选择Select Data，再在弹出的窗口中选择速度、加速度，即可显示速度、加速度与频率的二维表示。

用二维图除可表示某一节点的动态响应外，还可表示某一频率时全结构的位移和应力分布。图1-191表示的是第二阶固有频率（409Hz）附近400Hz的位移和应力值以及分布图。

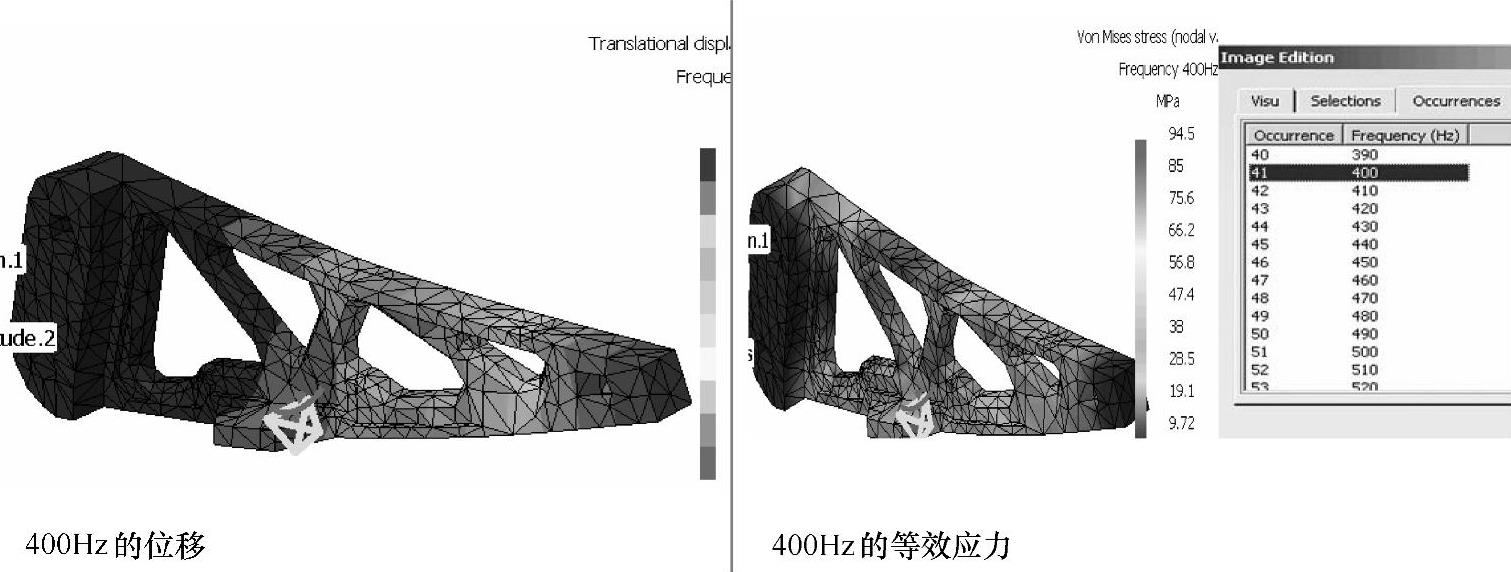
图1-191 动态调和响应的后处理

由于阻尼作用，并非刚好在固有频率时处达到最大值，常存在一定偏差。

在表示了位移或应力后，可对整个分析的频率范围进行动画表示。

本案例主要是对应试验室里的锤击试验而设定的外力激励的动态调和响应分析。动态调和响应分析也可是基础激励（见图1-192）。在此不作详细表述，读者可自己练习体会。

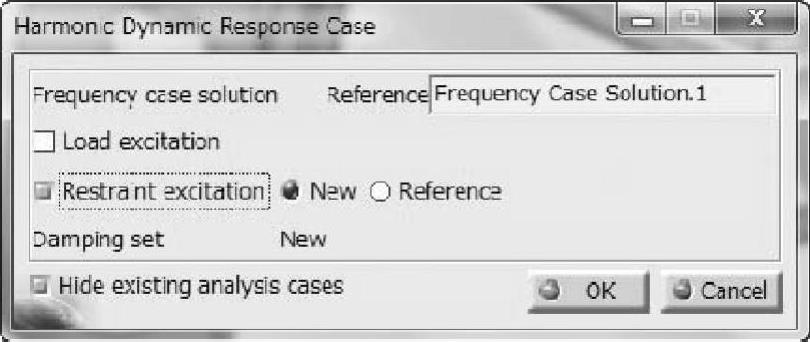
图1-192 基础激励的动态调和响应分析