数据选择器的实际应用举例

【例1】　用8选1数据选择器74LS151实现逻辑函数。

采用8选1数据选择器74LS151可实现任意三输入变量的组合逻辑函数。

作出函数L的真值表，见表3.3，将函数L真值表与8选1数据选择器的功能表相比较，可知只要将输入变量A、B、C作为8选1数据选择器的地址码A2、A1、A0，并且使8选1数据选择器的各数据输入D0～D7分别与函数L的输出值一一对应，就能实现要求的逻辑函数。即：

则8选1数据选择器的输出Y便实现了函数L。

接线图如图3.4所示。

表3.3　逻辑函数L的真值表

图3.4　用8选1数据选择器实现

L=A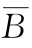+C+B

显然，采用具有n个地址端的数据选择器实现n变量的逻辑函数时，应将函数的输入变量加到数据选择器的地址端（A），选择器的数据输入端（D）按次序以函数输出值来赋值。

【例2】　用4选1数据选择器74LS153实现一位二进制全加器。(www.xing528.com)

全加器实现1位二进制的加法，它由被加数A、加数B和来自低位的进位数Ci相加，输出全加和S与向高位的进位Co。逻辑符号图如图3.5所示。

全加器的真值表见表3.4。

表3.4　全加器的真值表

图3.5　全加器逻辑符号

根据真值表写出逻辑函数为

根据74LS153的功能表，可知当使能端为低电平时，数据选择器的输出端1Y和2Y的逻辑表达式可写为

采用逻辑函数对照比较的方法，把全加器的逻辑函数与数据选择器的逻辑表达式相比较。如果把式（3.1）、式（3.2）分别与式（3.3）、式（3.4）相比较，则可以得出如下结果：若A接至A1，B接至A0，并且使双4选1数据选择器的8个数据输入端分别置为1D0=1D3=Ci、、2D0=0、2D1=2D2=Ci、2D3=1，则选择器输出端1Y、2Y分别实现了全加和S和进位Co。实验电路图如图3.6所示。

图3.6　用4选1数据选择器实现全加器

当函数输入变量数大于数据选择器地址端口数时，可能随着选用函数输入变量作地址的方案不同，而使其设计结果不同，需对几种方案比较，以获得最佳方案。