研究：波浪能发电机的发展和应用前景

有多种类型的发电机可用于将波浪能转换成电能。一般来说，在使用涡轮机为发电机轴提供机械驱动的系统内，通常使用同步发电机或感应发电机等旋转发电机。这些系统常用于近岸应用系统。在浮标式气动涡轮机系统中很少使用旋转发电机。在包括浮标在内的其他海上应用系统中，通常使用直线永磁发电机。不过，凸轮式圆柱波浪能转换器是个例外，虽然它们也是海上应用系统，这些装置使用的是旋转发电机。

4.3.5.1 波浪驱动式直线发电机模型

参考文献[37]提出了一种波浪驱动式发电机，它与交流发电机工作原理相同。该装置构成了通过电磁感应产生功率的两自由度机械系统。

前述发电机包括一个封闭在浮标内的电力发电机。该发电机具有由浮标框直接支撑的N匝矩形线圈和一个带有两个PM的系统，这两个PM由螺旋弹簧连接到浮标上，如图4.32所示。线圈在磁铁之间移动，而且磁铁构成了一个由波浪驱动的浮标运动所激励的两自由度系统。由于该系统没有旋转部件，因此不会产生任何缠结（Fouling）现象。

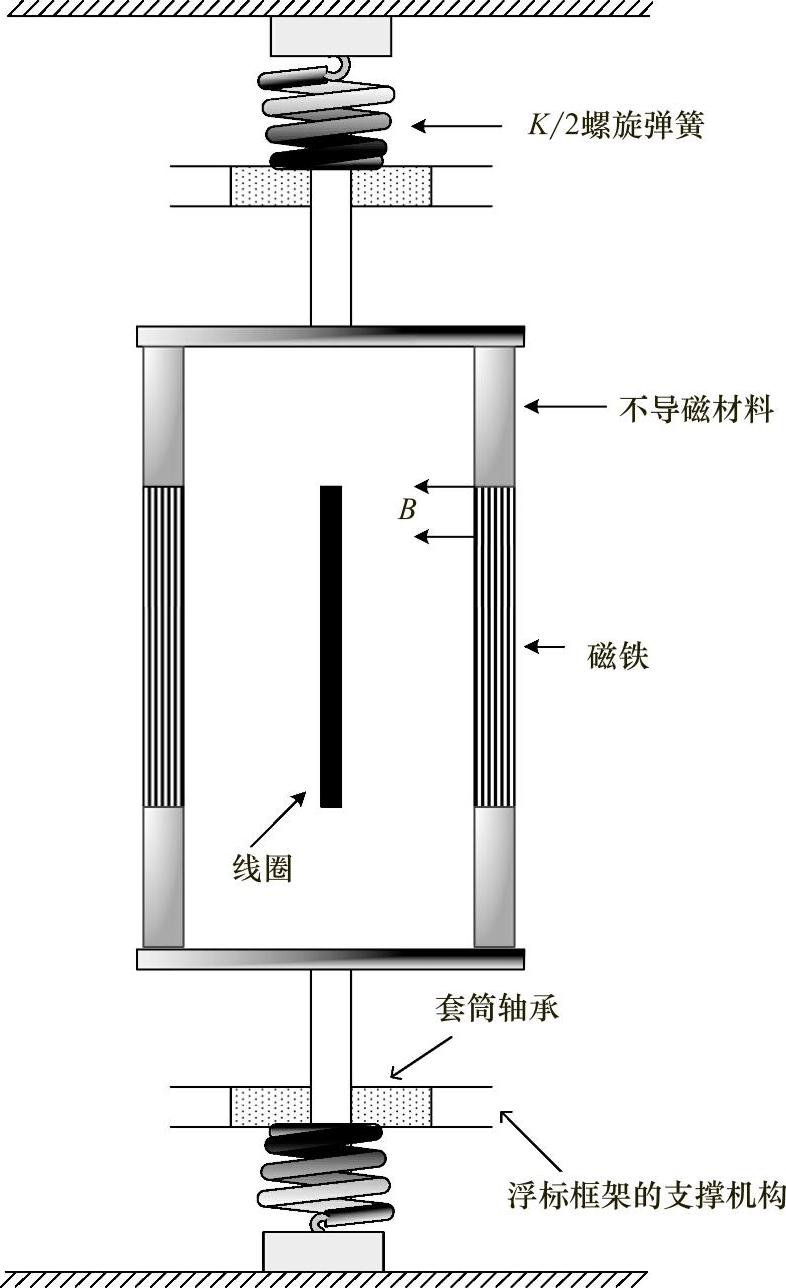
图4.32 线性波浪驱动发电机系统 （改编自T.Omholt，Oceans，10，585-589，1978）

导体相对于磁力运动而在导体中产生感应电流，这是产生电能的原因。

这类直线发电机产生的电能可以表示为

式中 V_r——线圈相对于磁铁的相对运动（距离）；

B——磁感应强度；

R——线圈内的负载电阻；

L——从平面垂向到平面表面磁场内的线圈长度^[37]。

由于电流的流动，一个作用力将被施加在线圈上以阻碍其运动，如式（4.47）所示。一个大小相等但方向相反的作用力也被施加在磁铁上：

一个浮标发电机系统的示意简图如图4.33所示^[37]。这类发电机内浮标的惯性力、阻尼力和恢复力之和等于励磁力。

阻尼力+惯性力+恢复力=励磁力（4.48）

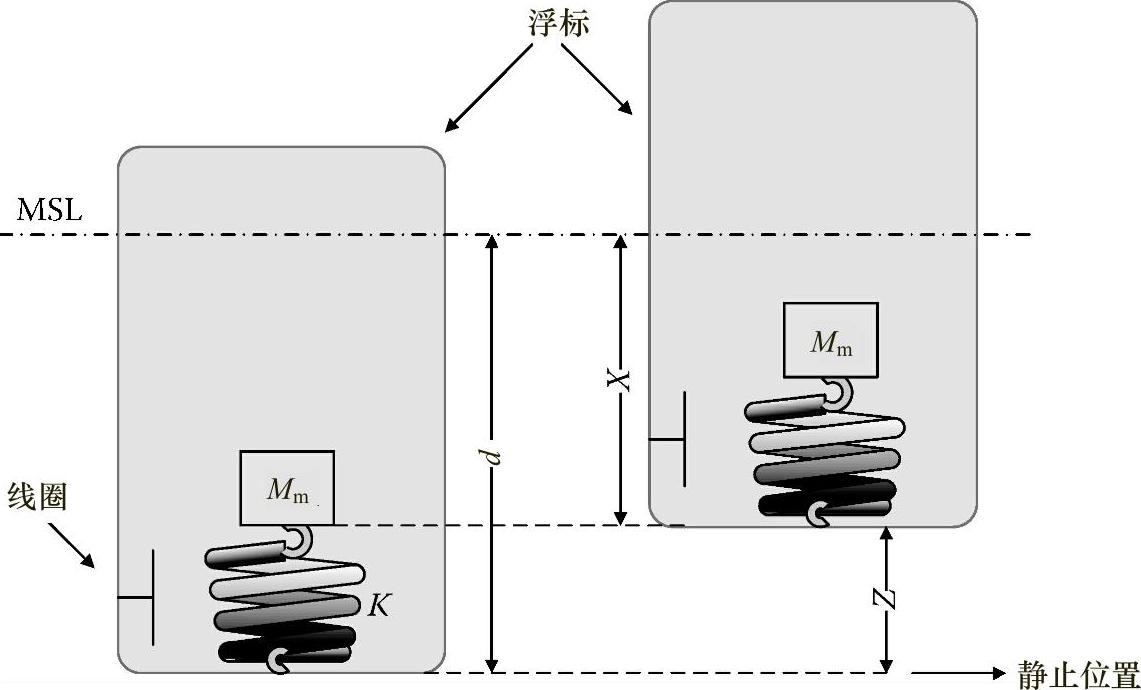
图4.33 浮标发电机系统示意图

下面的二阶方程描述了仅考虑无穷小波浪情况下的浮标发电机垂直运动的系统运动：

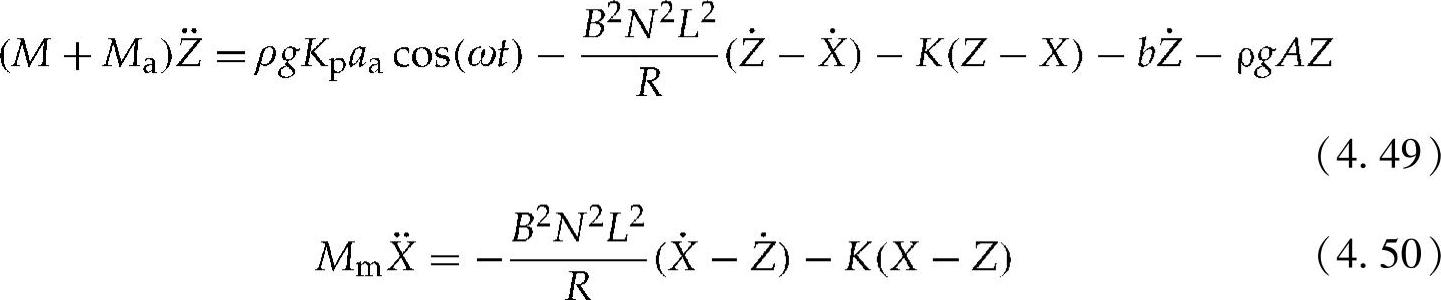
式中 （M+M_a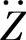）——惯性力；

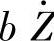——阻尼力；

ρgAZ——恢复力。

式（4.50）中右边所示为励磁力的总和，其中，m为浮标质量（不包括弹簧支撑的磁系统的质量），m_a为附加质量，b为阻尼系数，ρ为水的密度，K_p为压力响应因数（K_p=e^-kd），a为波浪的振幅，K为总的弹簧常数，ω为波浪频率，Z和X分别为位移，如图4.33所示。这些位移的微分即力相应的速度和加速度。假定该浮标直径小于波长^[37]。

式（4.50）基于以下假设：PM的质量为m_m，而且带有PM的系统是由感应力（F）激励的，而且该力通过螺旋弹簧来传递^[37]。由式（4.49）和式（4.50）可以看出，在X=Z或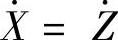的情况下，没有产生能量的运动。因此，X和Z的位移应该不同步，或者换句话说，两个运动之间的相位角必须大于0°但小于180°。

使用PM的系统由通过两个螺旋弹簧传递的作用力来励磁。它产生的电能可以表示为

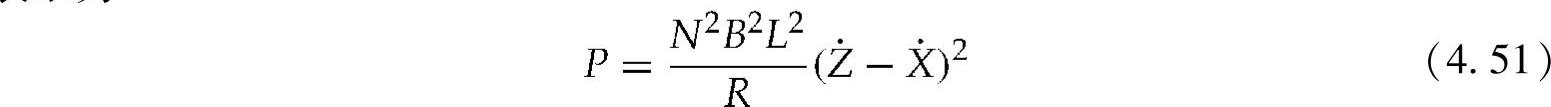
通过对式（4.51）中给出的能量方程积分，可以得到一个波浪周期T内的平均功率：

回顾由海浪携带的能量可以表示为P_W=ρg²a²TD/8π，因此，该系统的转换率可以表示为发电量占整个波浪能的比率，即系统效率：

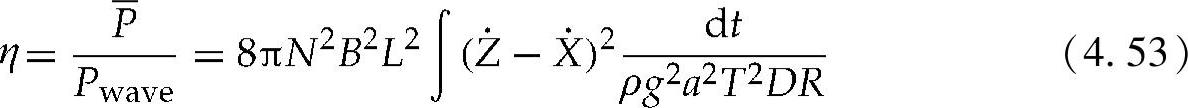
从这个效率方程可以看出，系统效率是浮标和线圈的相对速度与负载电阻的函数。在实践中，无论是流体的黏度还是弹簧常数都很小。它们施加的倾倒力远远要小于笨重的浮标。不过，对于较轻的线圈来说，这些影响几乎是不可忽略的。考虑到这些事实，该系统的运动方程可以简化为以下状态空间描述：

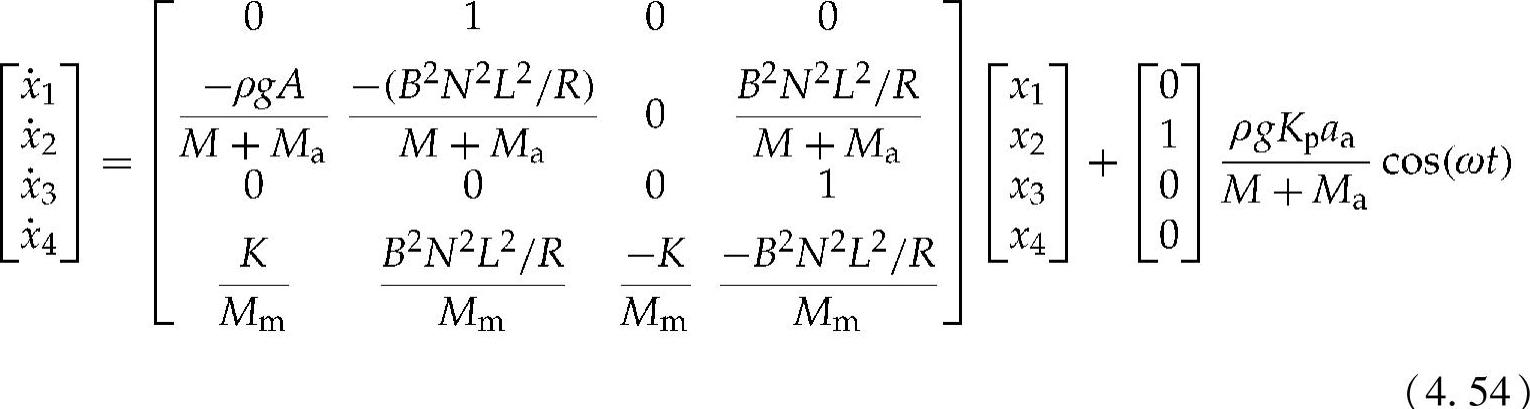
其中，可以使用下面的代换：

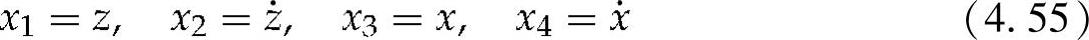
这些线性方程组在频域的通解由下式给出：

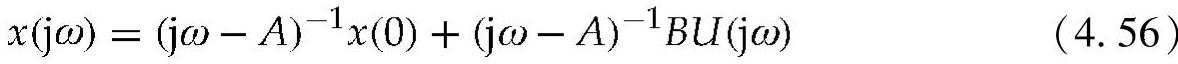
式中 A——状态矩阵；

B——输入；

x（0）——初始条件。

第一项描述了系统的瞬态响应，它在稳态响应下无效。第二项描述了系统在特定扰动下的行为。在这种情况下，假设海浪波在这种模式下的运动为正弦波形式。因此，该解将包括一个与输入正弦波频率相同的纯正弦波。在该频率下的系统频率响应确定的振幅和相位由下式给出^[38]：

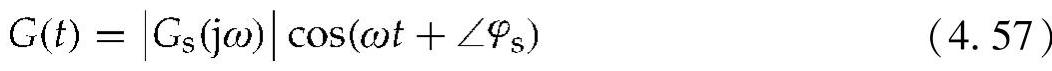
为了对该系统进行建模和仿真，可以将永磁直线发电机的参数和其他相应的物理参数选择如下^[38]：M=1344kg，M_a=119.5kg，L=2.64m，K=1，B=1.4T，A=4.86m²，N=30，D=2.5，K_p=0.9，a_a=1.5m，ω=2πrad/s。

代入这些参数，可以将状态转换矩阵写为

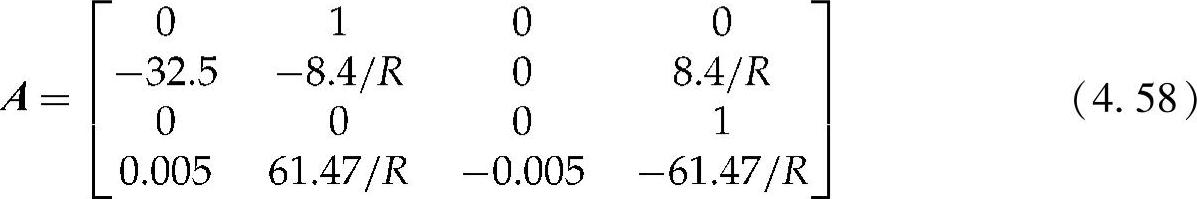
根据上述分析，运动方程的根可以计算如下：

这些解可以取代式（4.53）给出的系统效率方程，然后可以看出，系统效率是电阻R的一个复变函数。通过控制等效负载电阻值R，可以实现系统效率的最大化。

使用可变负载电阻值并代入式（4.61）～式（4.63），可以得出负载电阻对于效率和功率的影响。在仿真环境中，使用一个可变电阻来表示负载电阻对于提取的能量和效率的影响。使用一个正弦波源来表示海浪波形。在图4.34中，通过共享同一个X轴，给出了电阻—平均功率和电阻—效率的曲线图。

根据图4.34所示的结果，对于一个特定的负载电阻值，可以得出最大功率和最大效率值。在理想情况下，该系统应在此点上运行。为了实现这一目标，应该提供电流调节用于发电机的输出。图4.35所示的整流器和大电容提供了一个固定的直流电压，用作升压变换器的输入。假设使用的是无损变换器，可以控制输入电流来改变系统整流后的戴维南（Thevenin）等效电阻。

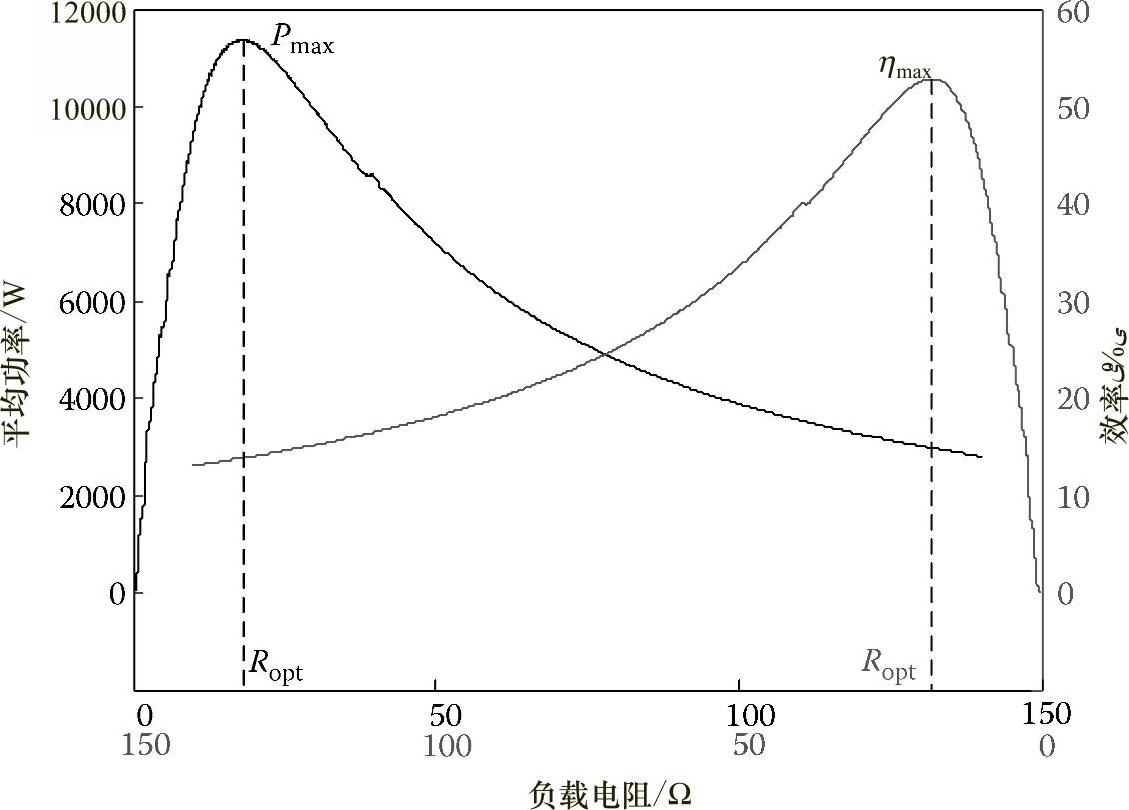
图4.34 平均功率和效率变化与负载电阻之间的关系

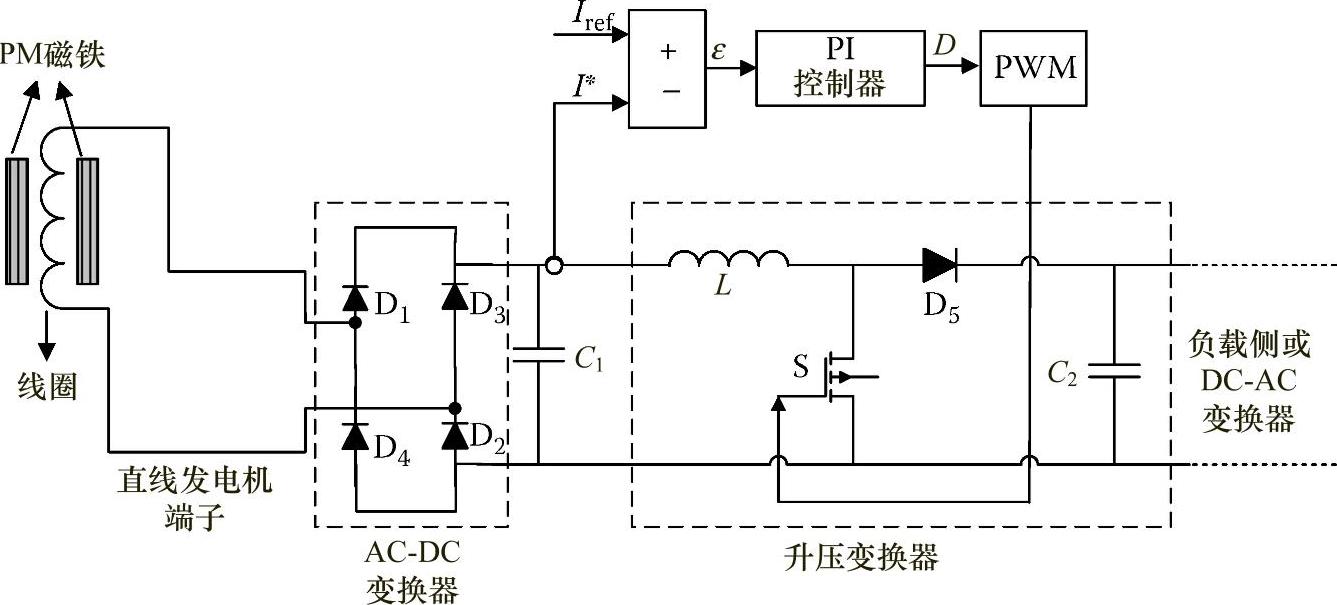
图4.35 直线发电机及能量变换器的系统结构图

发电机功率和发电机电压均为正弦波形式，分别如图4.36和图4.37所示。发电机功率为偏置正弦波形。

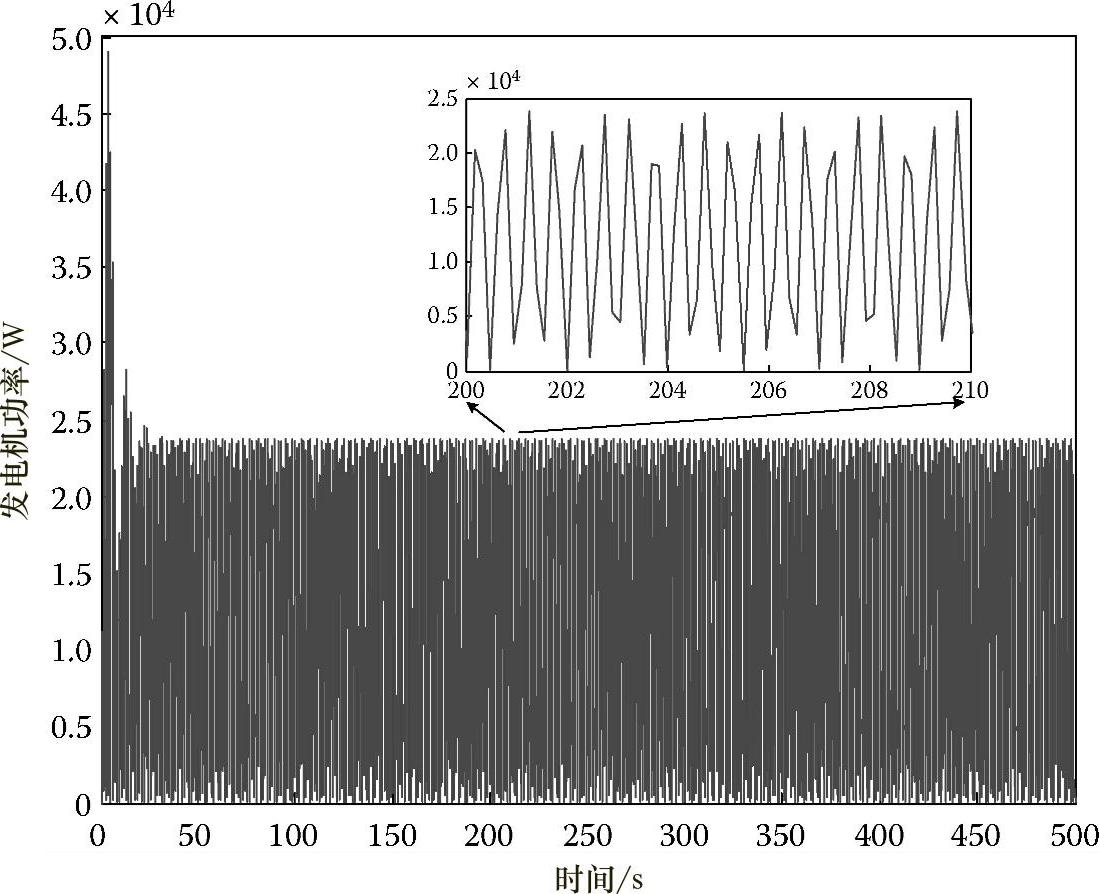
图4.36 发电机功率

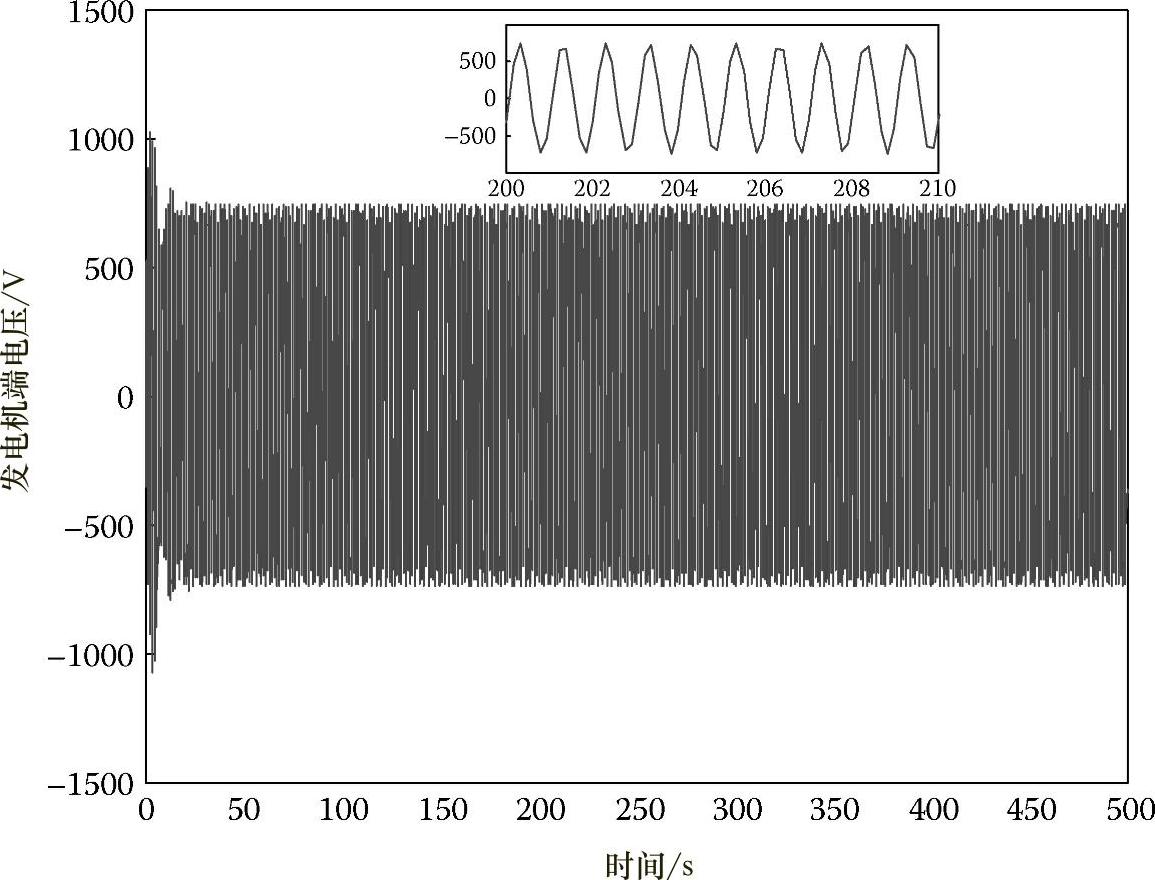
图4.37 发电机电压

为了调节发电机的输出功率和电压，直线发电机端子输出先被变换成直流电压，然后再进行滤波。考虑到该输出存在较大的振荡，需要使用一个大电容来实现令人满意的电压调节性能。系统使用了一个运行于电流调节模式的升压DC-DC变换器，因为使得变换器升压的输入电压是逆变器的输出电压，而且该电压为固定值。电流调节模式^[38]有助于直线发电机达到最优负载，因为等效戴维南阻抗是由变换器输入电压和电流决定的。

因此，无论输出与什么相连，通过调节升压变换器在固定输入电压下的输入电流，就可以调节其等效电阻。变换器的固定输入电压是由整流器和与发电机端子连接的电容器所提供的。图4.38所示为上述系统的电流跟踪性能。当电流达到参考值以满足最优的负载电阻时，其功率也随之增加并达到最大值。

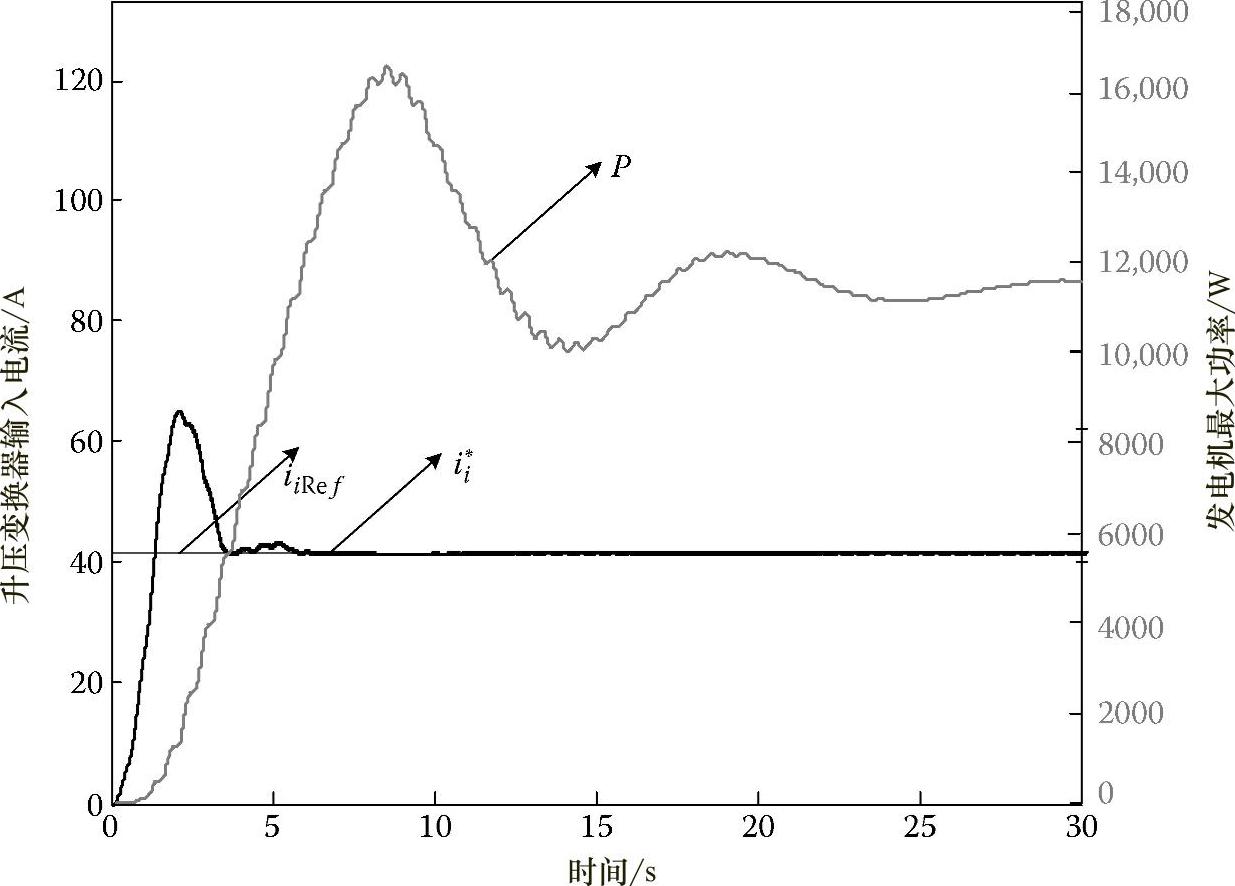
图4.38 直线永磁发电机的参考电流和输出功率跟踪

4.3.5.2 直线同步纵向磁通永磁发电机

直线同步纵向磁通永磁发电机是通过直接驱动将波浪能转换成电能的方法之一。在参考文献[39，40]中，穆勒（Muller）提出了一些用作波浪能转换器的直驱式直线发电机。对于WEC应用来说，直线纵向磁通永磁发电机的活塞通常由一个浮标来驱动。变幅变频电磁力是通过活塞垂直运动在定子绕组中感应而生的^[41]。可以通过连接多个机组（如阵列）来减轻变幅和变频带来的功率波动问题^[42]。

Wolfbrandt在参考文献[41]中介绍了一种带有二极管整流器的纵向磁通永磁发电机（LFM）的设计和建模系统方法，其中活塞使用一个浮标来驱动。

一个波浪周期T内的海洋波浪平均能量可以使用式（4.61）给出的波浪总能量来求得。当浮标被部署成一个乘波体时，该浮标的功率可以近似为

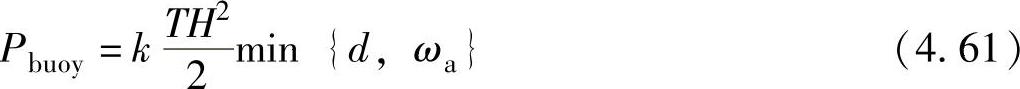
式中 k——吸收系数；

d——浮标直径；

ω_a——可吸收最大能量的浮标宽度。

如果浮标被当作一个点吸收器，波浪被假定为正弦波，而浮标的位移是在一个方向上，那么（例如k=0.8），实现50%的功率吸收是可能的^[43]。吸收宽度定义为^[44-46]

式中 L_wave——波长，定义为

这个方程对深水有效，也就是说，其深度大于波长的一半。在深水中，波浪的动能等于其势能。Wolfbrandt^[41]研究了一种经过二极管桥式整流器整流的带有直接驱动的表面安装型PM三相LFM。图4.39所示为该发电机一个磁极的x-y平面横截面视图。

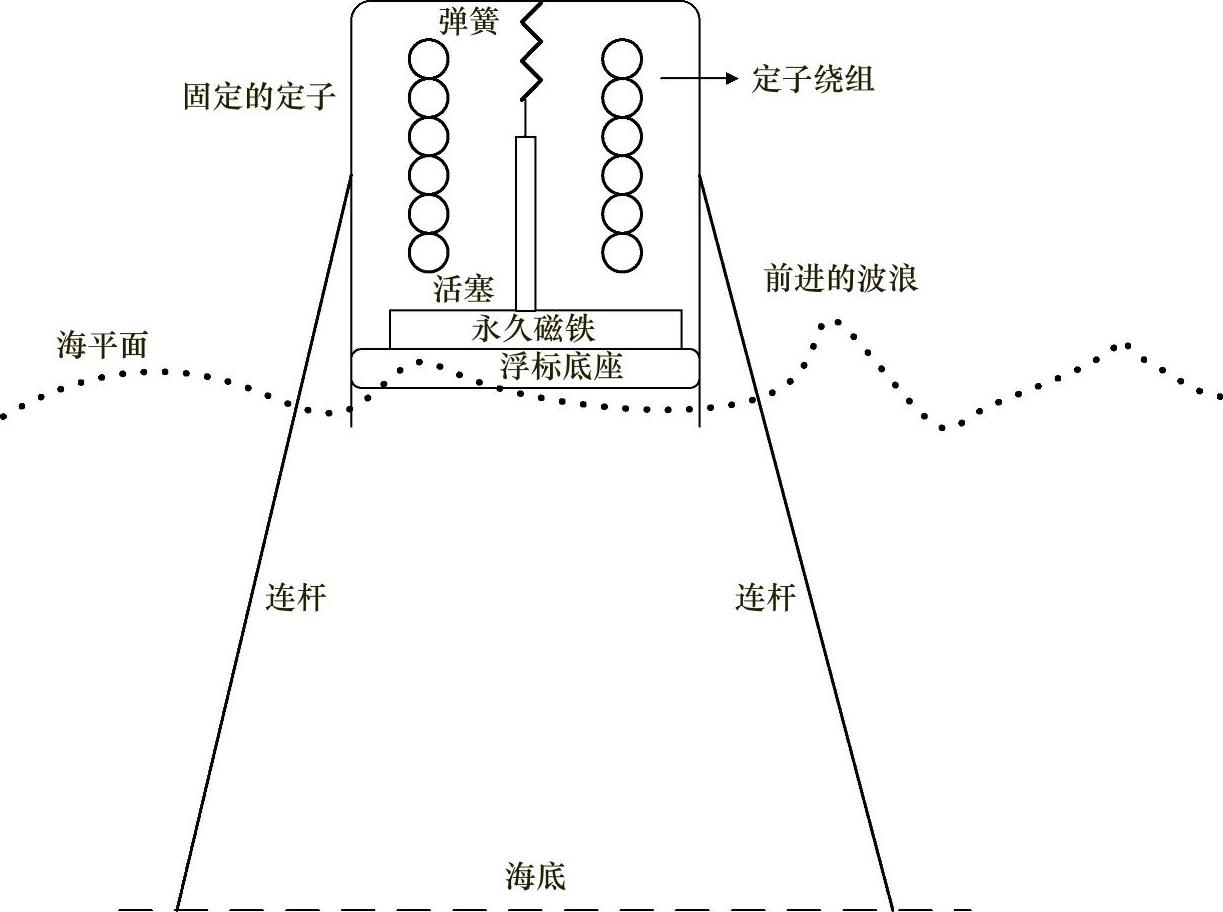
图4.39 用于WEC的LFM示意图

在此方法中，直线发电机的定子由一个固定在海底的浮标来支撑。前进的波浪驱动活塞，这将导致PM上下运动。这样就产生了一个电磁场，而且在定子绕组端产生感应电压。

定子内的磁通强度在靠近PM的线圈内较高，外部的线圈绕组磁通强度变弱。这种PM产生的磁通强度如图4.40所示。

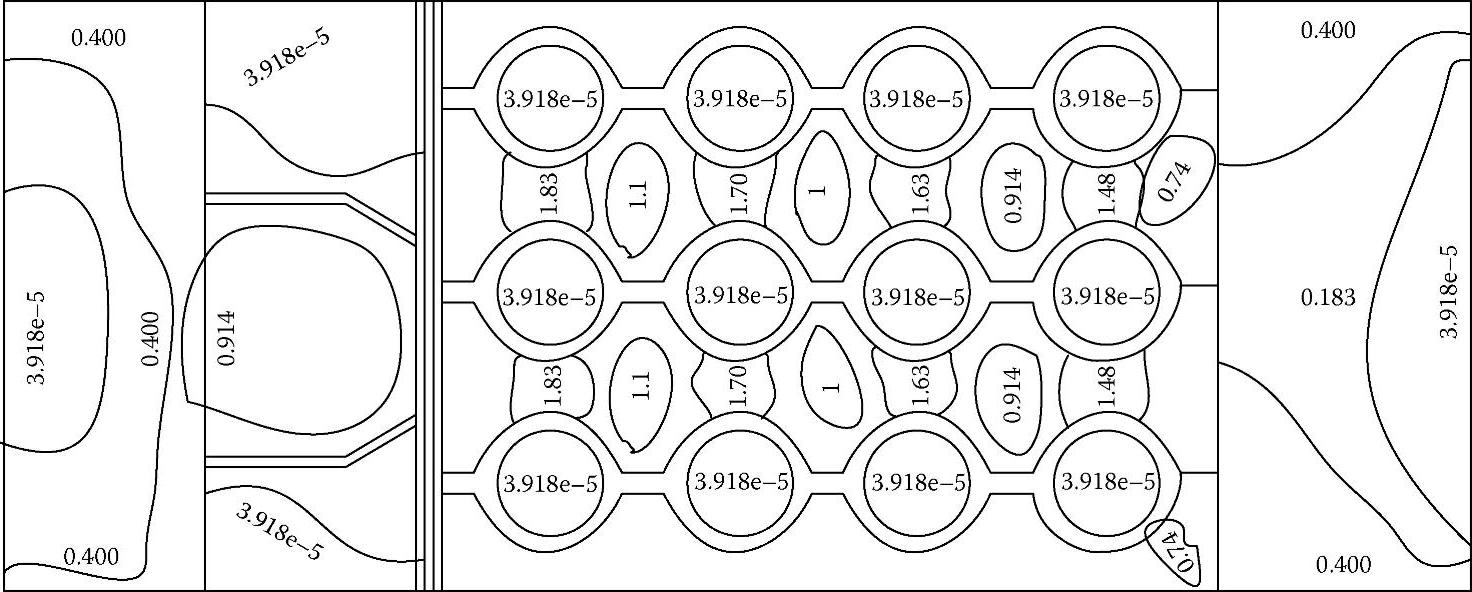
图4.40　PM创建的近似磁感应强度（Wb/m²）

还有其他几种拓扑结构也使用了与直线发电机系统相同的工作原理。例如，可以将固定的定子绕组安装在一个磁轭上，该磁轭通过一个支撑装置固定在海底。在此方法中，PM通过系绳与浮标相连接，该浮标在海平面上下移动，而且可以被海浪向不同的方向拖动。一旦浮标被波浪驱动，浮标就会拉动PM活塞。PM在固定的定子绕组之内上下移动，这样就产生了一个可产生电能的电磁场。这种能量转换装置的原理如图4.41所示。

由于波浪周期相对较长（活塞低频运动），位移电流可以忽略不计。基于麦克斯韦方程

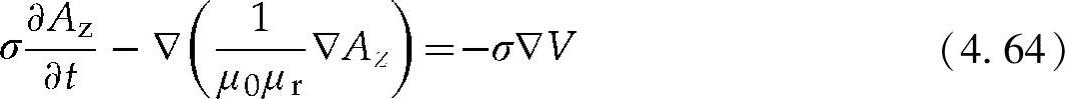
式中 A_z——磁势矢量的z分量；

μ0——自由空间的磁导率；

μ_r——相对磁导率；

σ——电导率；

——应用势能。

电流源可用于PM建模。定子绕组的端部效应可以被建模成电路的阻抗。端部效应是影响直线发电机发电性能的因素之一。定子绕组方程可以表示为

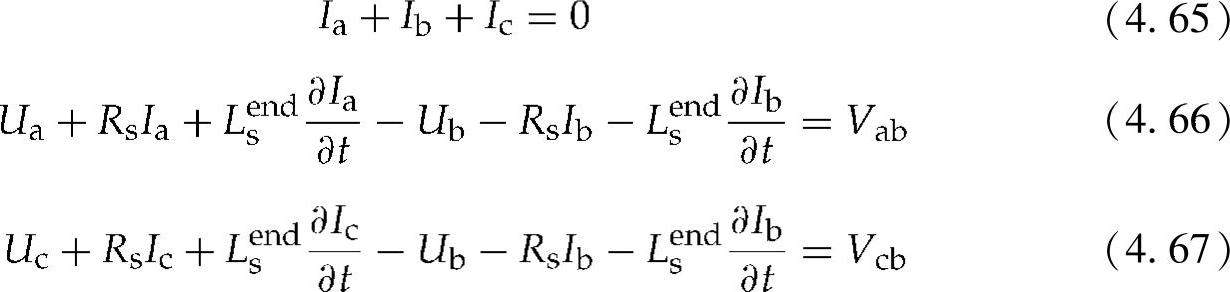
式中 I_a、I_b和I_c——相电流；

U_a、Ub和U_c——相电压；

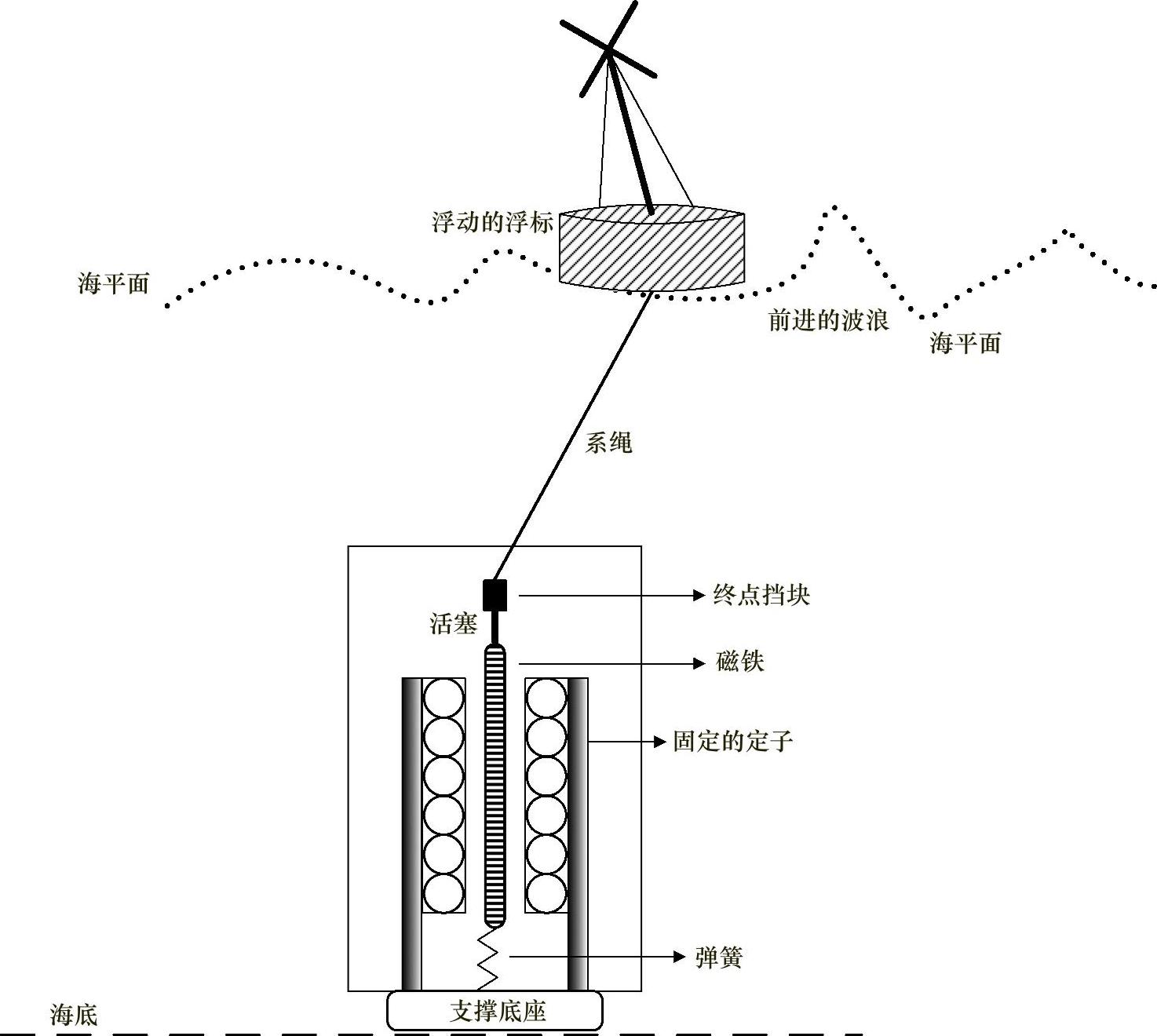
图4.41 另一种用于WEC的LFM示意图

V_ab和V_cb——线电压；

R_s——线电阻；

L_s^end——线圈端电感。

直线发电机的输出相电压可以采用三相二极管整流器来整流，而且可以与负载相连接。与负载相连的一个全桥六脉冲二极管整流器如图4.42所示。在图4.42中，负载元件包括电阻（R）、电感（L）和反电动势（E）。

直线发电机的损耗大致可分为铜损和铁损两大类。这些损耗的功率流如图4.43所示，其中，P_gen为发电机的理想输出功率，而P_out则为发电机的实际输出功率。

定子绕组线损耗可以分为欧姆损耗（P^o_Chumic）和涡流损耗（P^j_Couule）。这些损耗方程可以表示为^[41]

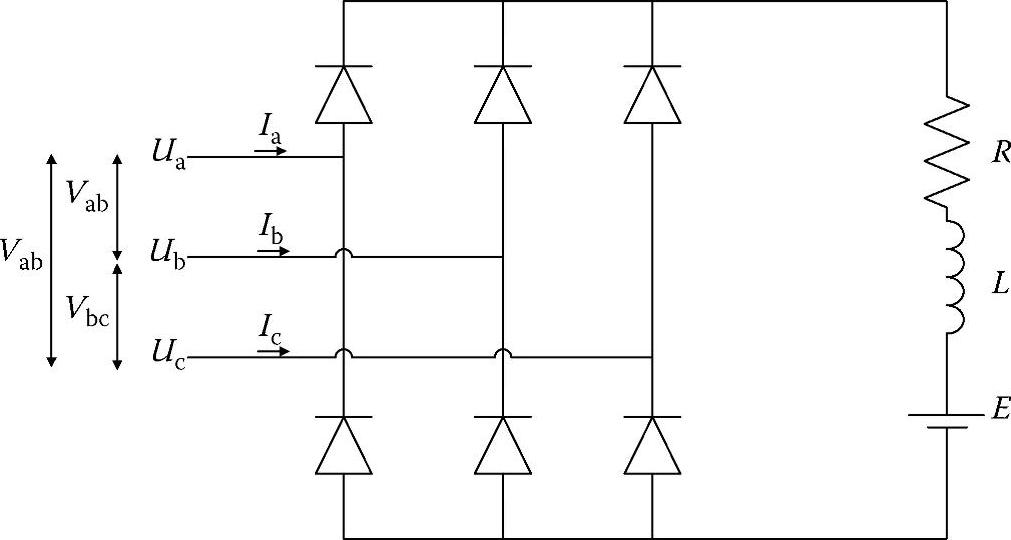
图4.42 三相二极管整流器示意图，其中a、b和c为直线发电机各相

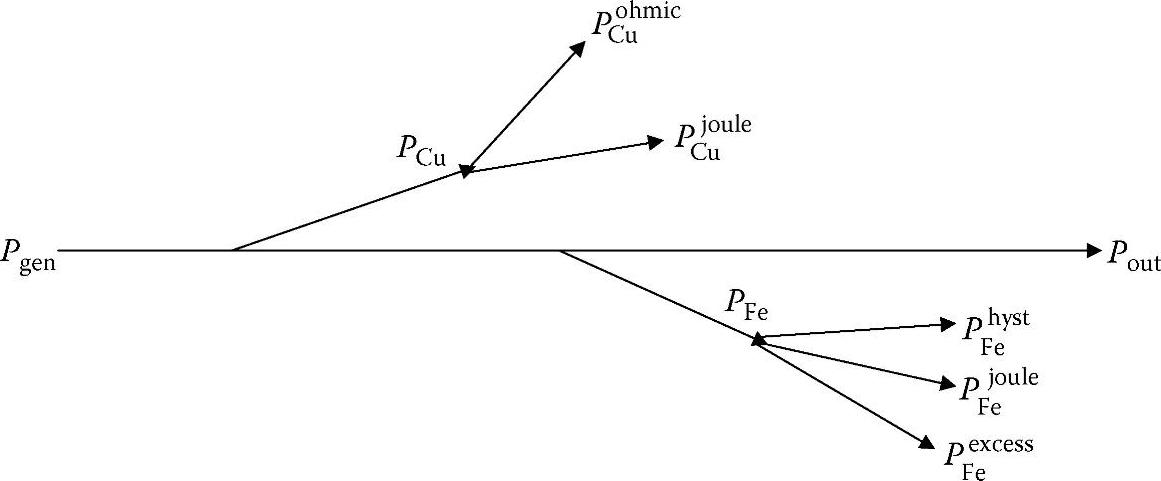
图4.43 直线发电机的功率流和损耗

式中 ω——角频率；

d——单线直径；

S——导体截面积；

B——磁场密度。

可以使用一个单值的磁化曲线对叠压铁心的非线性进行建模。铁损可以分为磁损耗P_Fe^hyst、焦耳热损耗_PFe^joule以及附加损耗PF_e^excess[47]。这些损耗由下列方程给出：

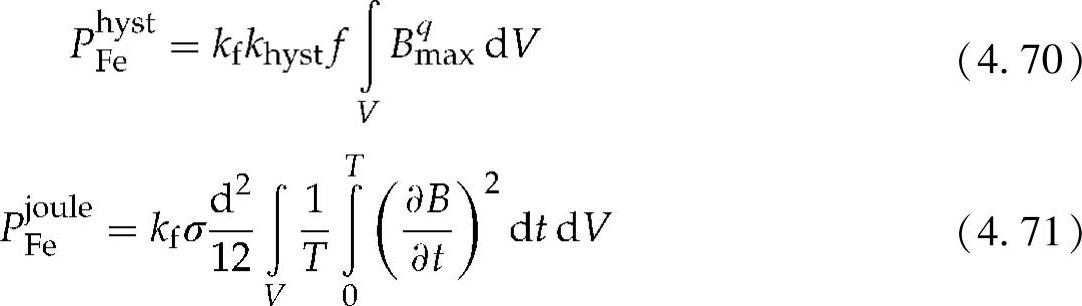
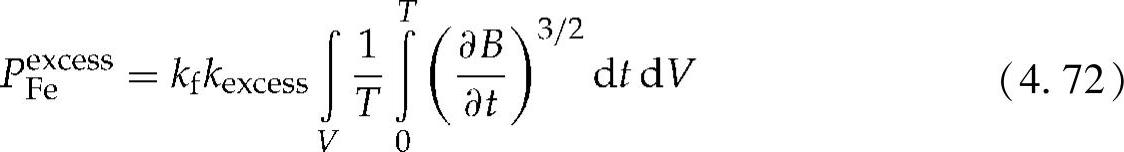
式中 B_max——磁场密度最大值；

f——频率；

d——板材厚度；

k_f——叠压系数；

T——时间周期；

V——定子铁心体积。

系数k_hyst（Ws/T_q/m³）、k_excess（W/（T/s）3/2/m³）和指数q由某一给定的损耗曲线来拟合。

在背铁、PM和铝槽楔中的活塞损耗可以使用坡印亭（Poynting）矢量来计算。因此，焦耳损耗P^joule_piston与磁滞损耗P^hyst_piston为

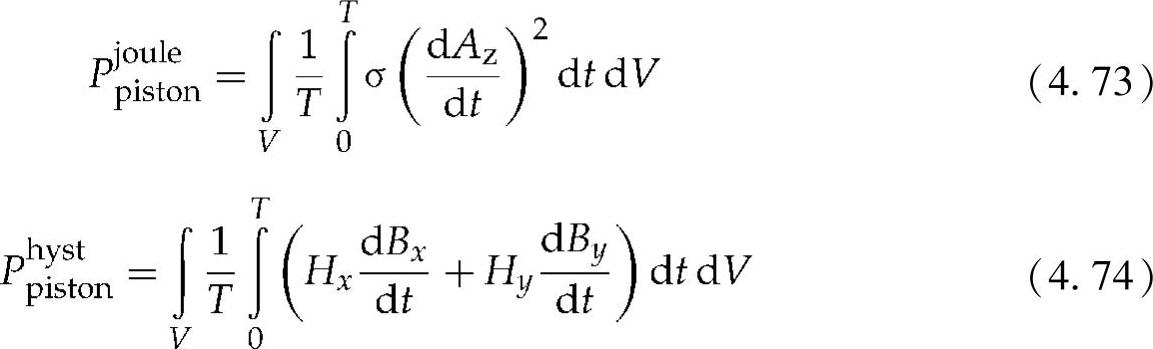
式中 T——时间周期；

V——活塞体积。

由发电机感应的电磁力F_em可以表示为

式中 W_C——气隙量的伴随能（Coenergy）；

x——活塞位置。

定子电流波动将会引起电磁力波动。由相带磁动势空间谐波引起的这些波动，可以通过分数齿槽节距绕组来消除。

带有不同电压负载的LFM会产生不同的电流密度。由于直线发电机的物理限制，电流密度上限为i_max。由于这一限制，发电机的功率输出将受到以下限制：

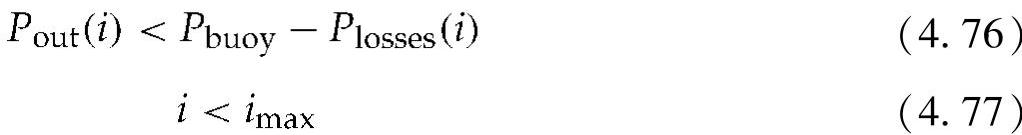
P_buoy在式（4.61）中定义，而P_losses则被定义为式（4.68）～式（4.74）给出的损耗总和。

图4.44所示为它们相对于最大电流的功率。实线为输入功率（浮标功率），虚线为输出功率，点线为输出功率和损耗的总和，代表总功率。

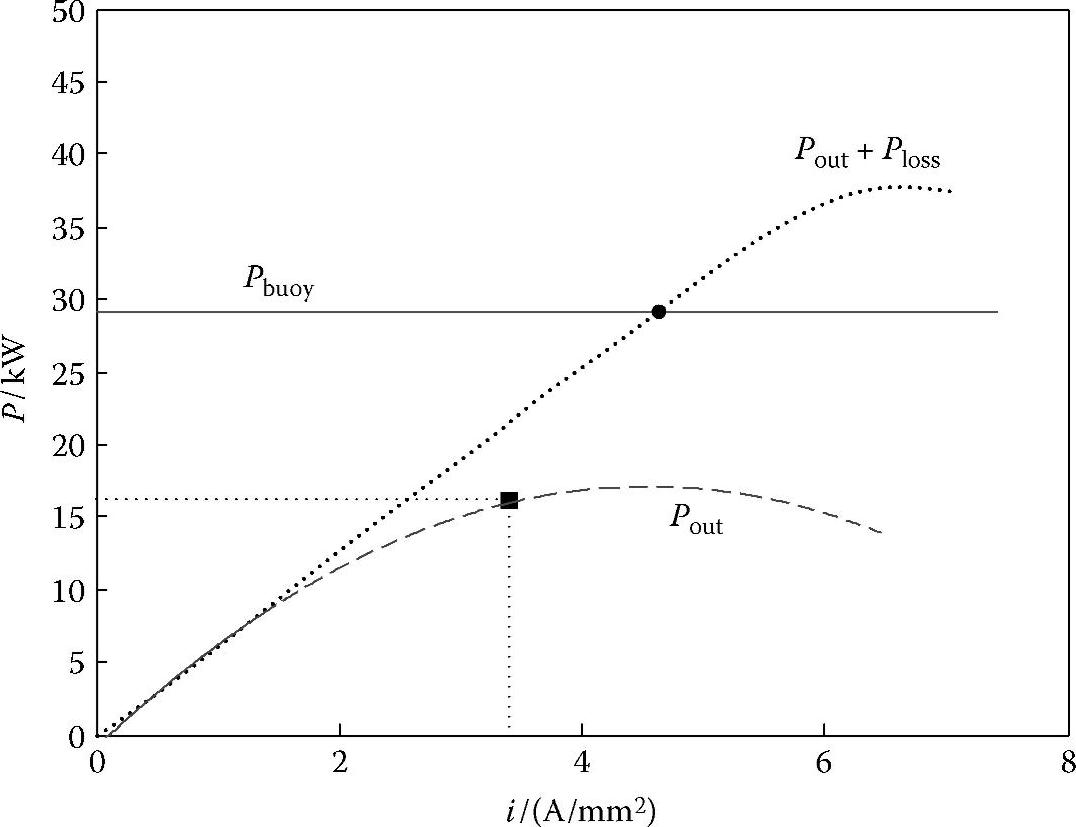
图4.44 浮标功率和输出功率与电流密度之间的关系

4.3.5.3 用于海洋波浪应用系统的三相同步发电机

同步发电机通常以恒定速度在发电站使用。对于波浪能应用来说，参考文献[48]给出了绕线转子无刷同步发电机的结构设计和相关模型。

在同步发电机中，转子转速和输出功率频率之间的关系为

式中 f——输出频率；

p——凸极数；

n——转子轴转速（r/min）。

因此，对于一个双凸磁极发电机来说，同步速度将达到3600r/min^[48]，因为该系统的输出频率应为60Hz以便实现并网。电枢励磁产生交流电，而且该电流被变换成直流电，使得电枢励磁器可以作为励磁绕组的直流电源。电枢励磁器有三相绕组，与单相整流相比，这样可以获得效率更高的三相整流。

在这种发电机中，凸磁极面是带式的，因此气隙宽度在其极点中心可以达到最小值。磁通量在最小气隙处达到最大值。磁通在两个磁极之间的中点处减小到零，并在相邻磁极中心达到负最大值。气隙内的磁通密度为正弦形式：

式中 y——垂直轴相对于转子的固定坐标；

β——转子磁通角；

D——气隙直径。

因此，磁通密度方程可以改写为

图4.45所示为定子绕组中的感应电动势，沿着其外围形成正弦磁通分布。因此，坐标x处的磁通量相对于定子是固定的^[48]。

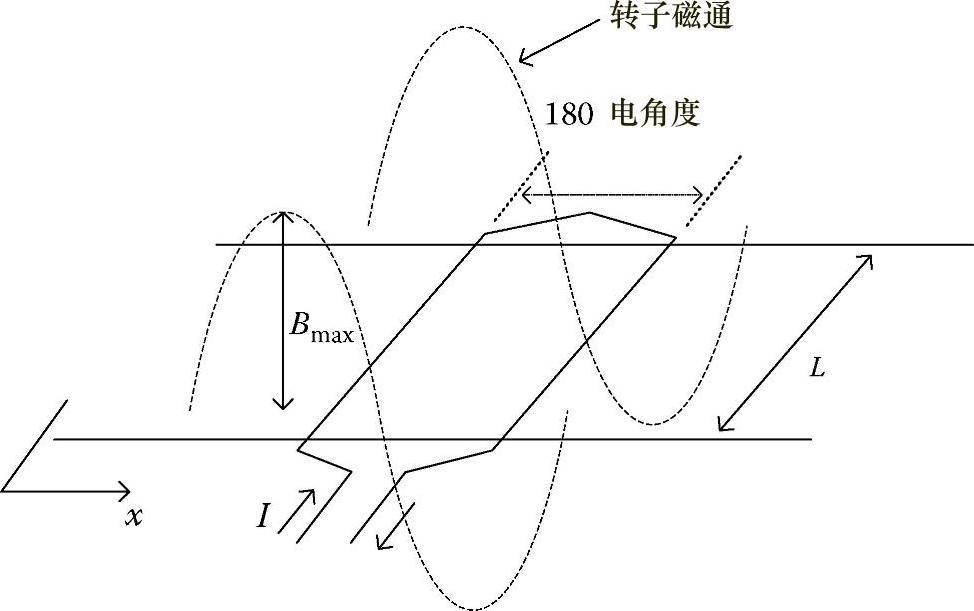
图4.45 定子绕组的磁通行波

定子绕组的坐标和转子位置如图4.46所示。

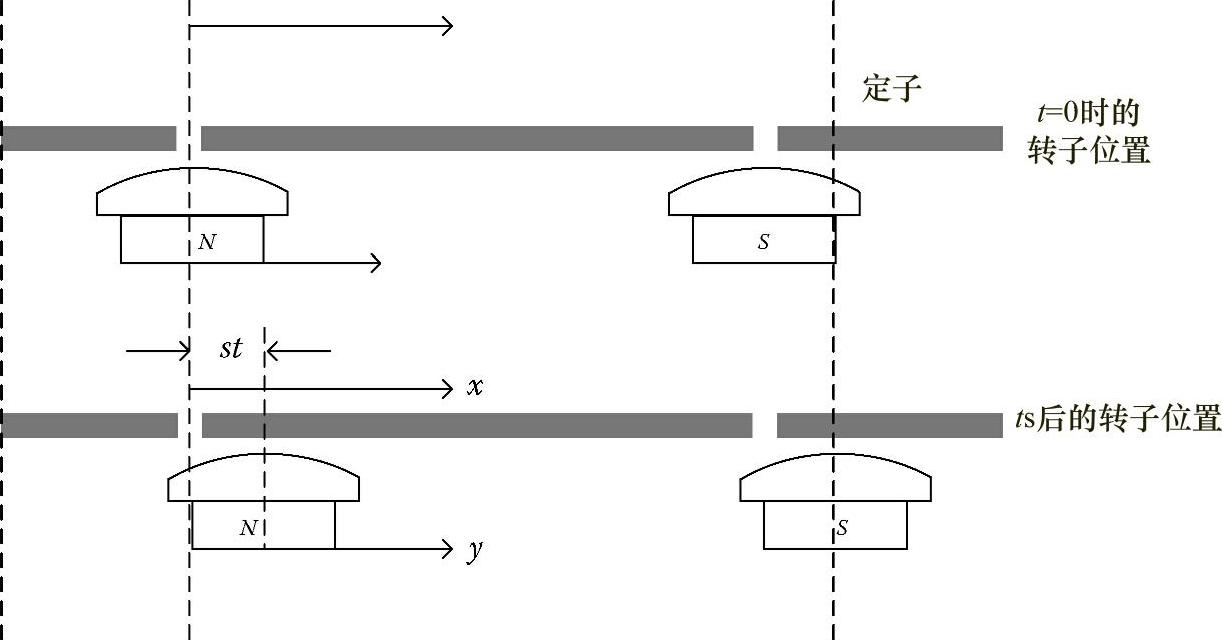
图4.46 定子绕组的坐标和转子位置

从图4.46中可以看出

其中　转子的切向速度s为

因此

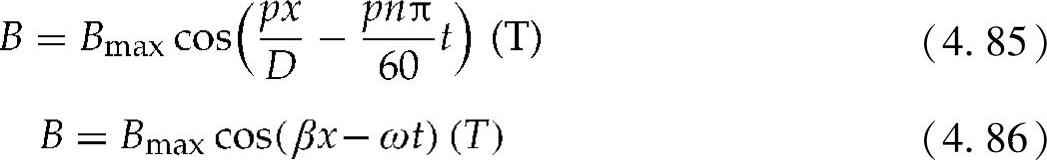
其中

这是感应电动势定子绕组中行波的数学表达式。通过宽度为dx的微分空间窗口的微分通量为

式中 L——转子的轴向长度。

通过线圈的总磁通量为

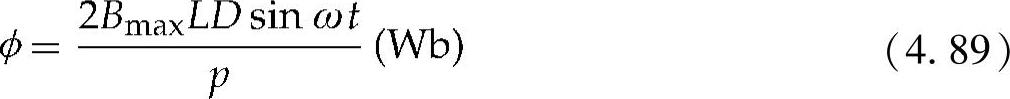
等距齿槽感应的总电动势可从式（4.88）得出：

式中 N——定子绕组的匝数。

产生的电动势有效值可写作

图4.47给出了通过将定子绕组放入分布在周边的多个齿槽中来利用整个定子表面的一种实用结构设计。

这些齿槽都以α电角度相位角来放置，而且总体上每个磁极有q个齿槽。将这些线圈串联起来可以得到总电动势。感应电动势取决于齿槽的α。因此，通过计算复相量E₁、E₂等总和，可以得到总电动势E。

分布效果和电动势相量E如图4.48所示。

因此，相量E的分布效果可以通过所有的感应电动势来求得。相量E可以根据下式求出：

复相量E的有效值为

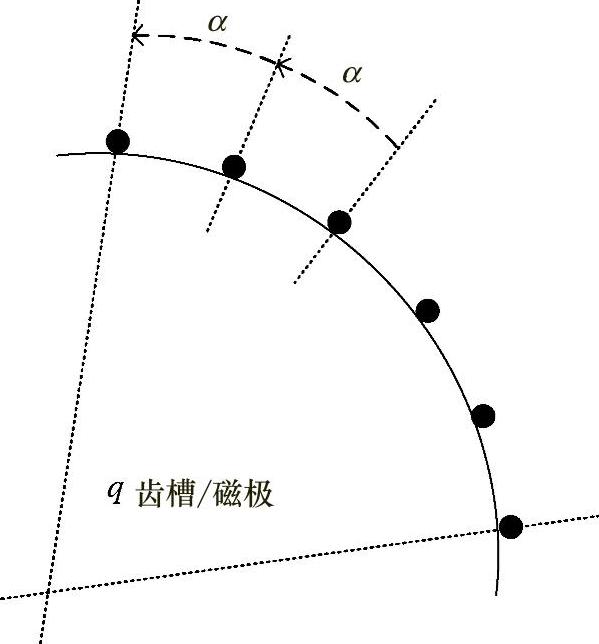
图4.47 定子表面总体和环绕周边的q齿槽

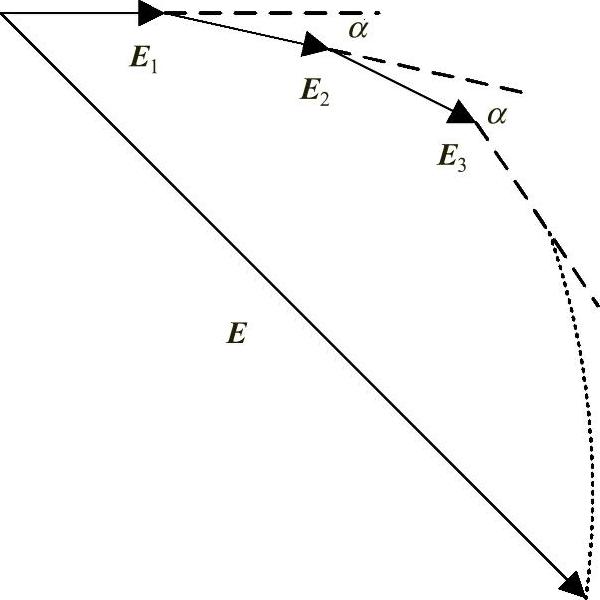
图4.48 总电动势相量

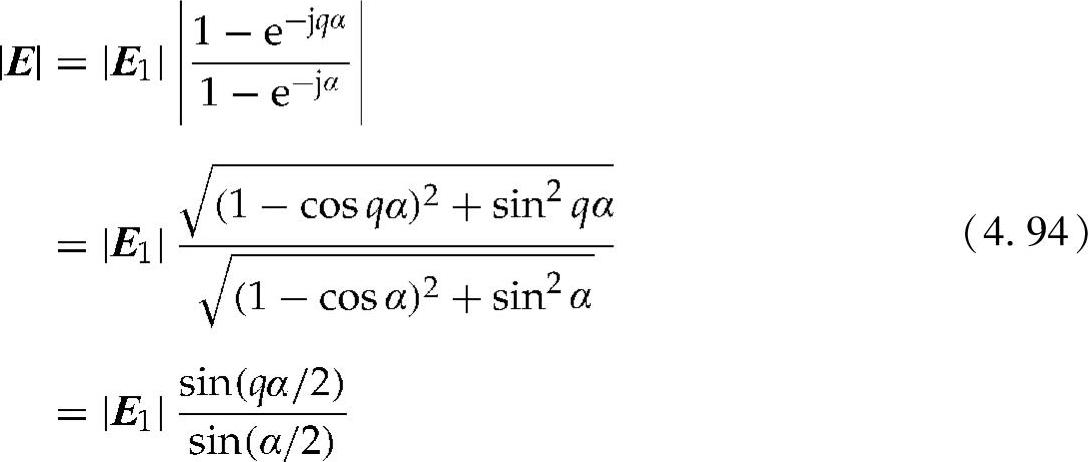
单相定子绕组磁心和线圈布置如图4.49所示。

在图4.49中，每个不同的磁极对都与绕组感应电动势的E_q成分有关。总电动势E为所有电动势E_q的矢量和。图4.49表明，有两组线圈，每组线圈在每磁极每相上都有6个线圈。

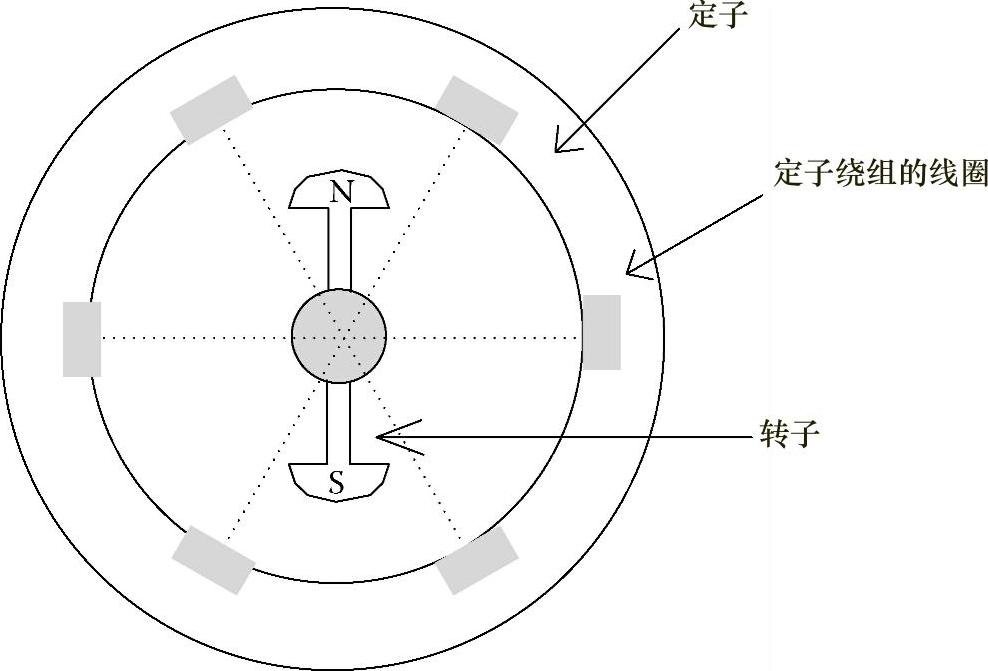
图4.49 每相的定子铁心结构和定子绕组布置

输出功率由三相共享。当负载连接到发电机端时，可由下式给出电压降：

V=E-IZ （4.95）

式中 V——端电压；

E——感应电动势；

I——定子电流；

Z——阻抗。

电枢励磁和电场励磁对于无刷同步发电机是非常必要的。如果要产生更大的输出功率以及降低输出频率，可以使用更多的磁极数以供励磁。如果频率纹波较高，磁通可能会失去其稳定性。

在这种发电机结构中，使用6个用于电枢励磁和电场励磁线圈的磁极以降低频率纹波。励磁电路如图4.50所示。

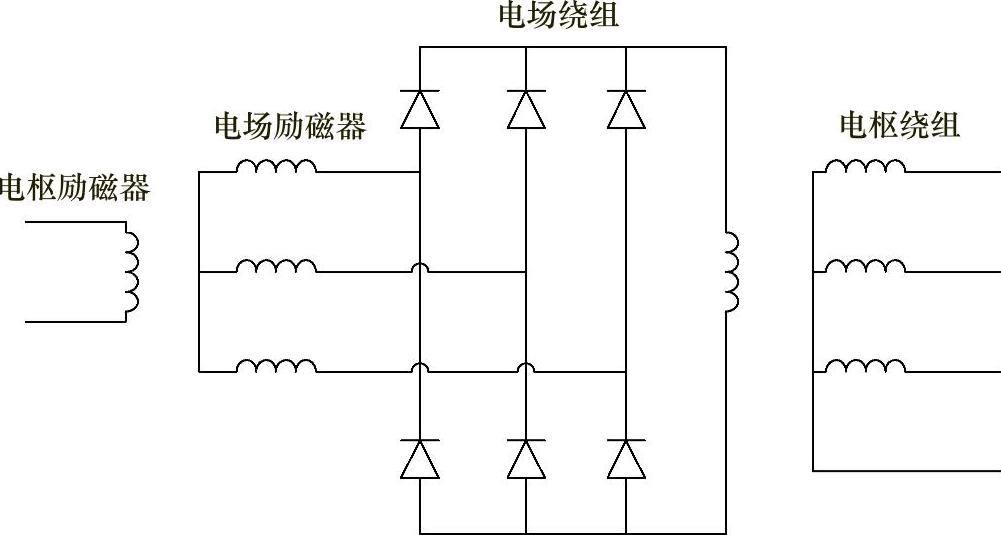
图4.50 使用电枢励磁和电场励磁系统的无刷发电机绕线转子示意图

发电机绕组的电阻和电感会影响功率损耗I²R，进而又影响到发电机的效率。因此，定子绕组的匝数（N）和铜导线的厚度将会影响到等效电阻和电感。

电阻和铜损可估算为

式中 D_w——电线直径；

I——绕组中的电流方均根值；

l_w——绕组长度，l_w可由下式计算而得：

式中 D_av绕组的平均直径。

在发电机结构设计中应该考虑的另一种效应是趋肤效应。趋肤效应是指电流流动将更加接近导体外表面的趋势。在低频段，可以假设电流为均匀分布。铜线的厚度应根据输出频率来确定。

涡流损耗和磁滞损耗是在发电机叠压铁心结构设计中应当考虑的其他因素。磁导率较高的叠压铁心更适用于增大磁通密度，同时还能够降低发电机的尺寸大小。

图4.51所示为某些软金属的磁通密度B与磁场强度H之间的关系图。由于高速发电机（3600r/min）较之低速发电机损耗更小，因此其总输出功率便会增大。

可以使用薄层叠压软磁材料来设计更为高效的发电机磁心。这也可以减小叠压磁心的机械应力和热损耗。

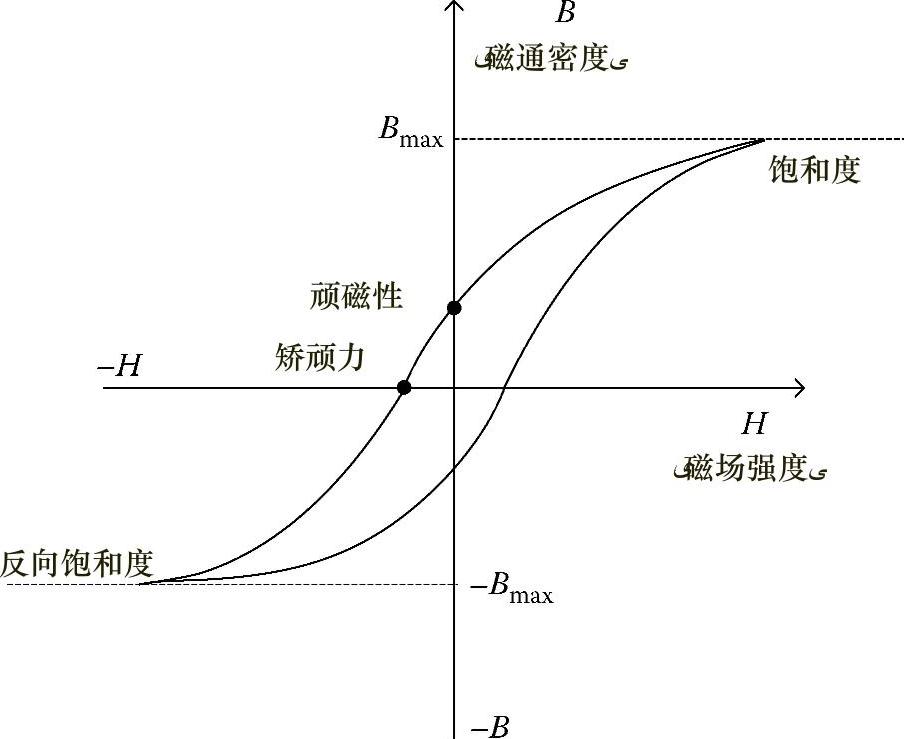
图4.51 磁通密度B与磁场强度H之间的关系图

4.3.5.4 用于WEC的径向磁通永磁同步发电机

本节将介绍一种带有水平轴水轮机的径向磁通发电机。图4.52a和4.52b给出了一种由发电机环绕的涵道式水轮机方案图^[49]。(www.xing528.com)

一些较旧的技术采用的是轴流式水轮机与类似风力机的发电机相耦合的方式。它们需要使用变速箱将常见的转子转速（10～20r/min）提升到传统的发电机转速（500～1000r/min）。不过，直接驱动是一种具有吸引力的解决方案，用以消除复杂性、故障率、效率及维护成本等方面的问题^[49]。

在直驱式水轮机拓扑结构中，机器的活动部件被叶片的边缘所包围，而不是像传统方法那样将它们放在水轮机轴上。参考文献[50-52]研究了这种方案，它已在船舶推进方面获得成功应用。有些轮缘驱动的推进器已用于自主水下机器人和船舶推进系统。参考文献[49]中已经对一个带有额定功率为50W的水轮机的类似发电机进行了测试。

参考文献[49]中所述结构的好处之一是取消了变速箱。变速箱最多可以达到三级，这使系统变得很复杂，而且该部件也非常笨重和昂贵。有叶片环绕的低速发电机直接驱动应用系统，导致了高额定转矩的出现，它与经典直驱式发电机相比，通常会更加笨重，而且效率很低^[53]。此外，通过将发电机保持在一个保护管道中，可能会提高叶片的水力效率，振动和空化性能也会得到提升^[52]。将转子的运动部件放置在叶片周围，不仅导致了发电机气隙直径增大，而且该发电机还将具有较高的转矩。与在转速Ω下产生功率P的水轮机相耦合的发电机转矩为

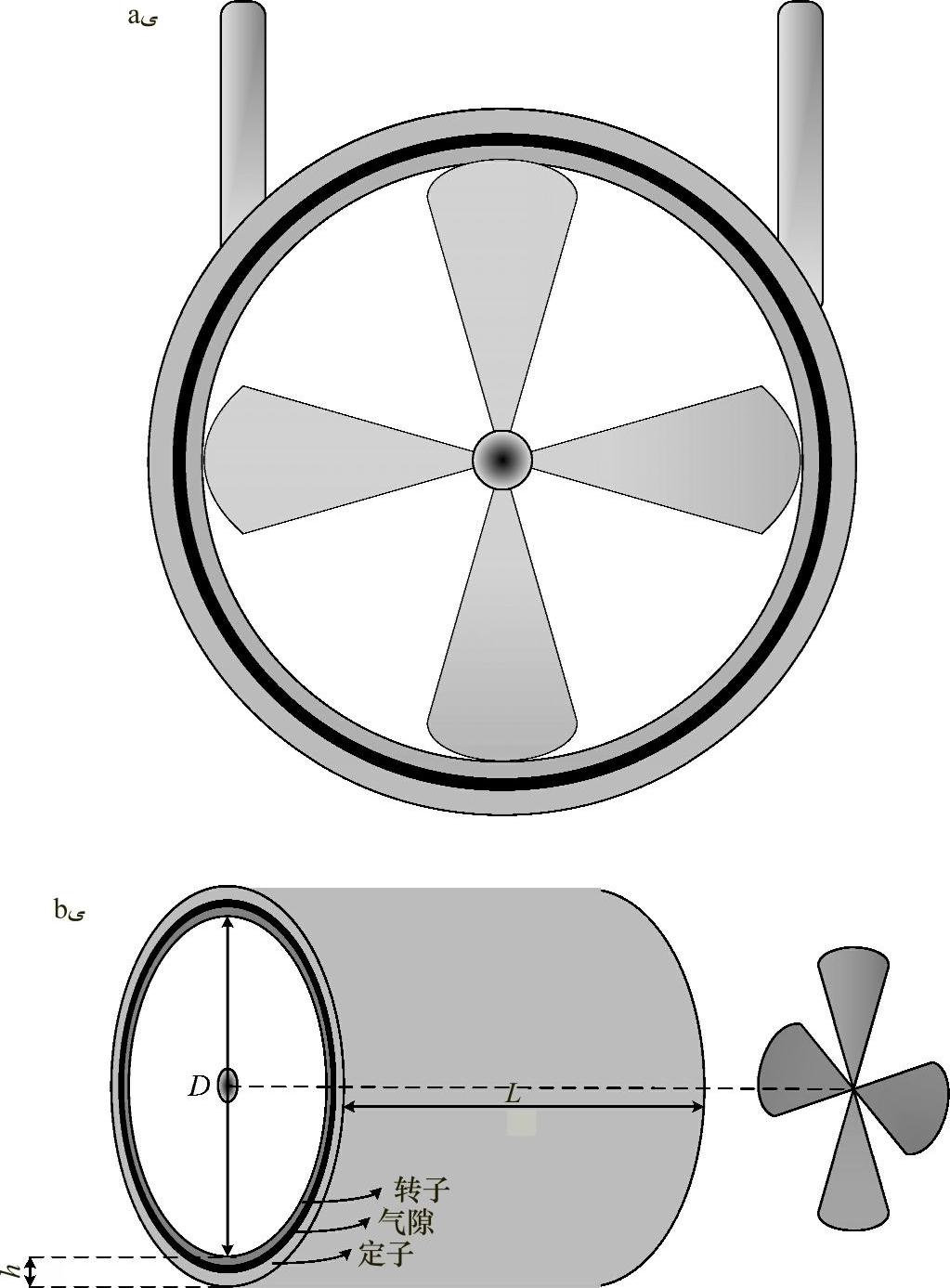
图4.52 放置于水平轴水轮机叶片边缘的径向磁通发电机

a）正视图 b）侧视图

转子和定子之间靠气隙分离，在气隙中产生电磁相互作用。气隙中的切向力密度σ_t取决于发电机技术和冷却系统。使用切向力密度，电磁转矩可以表示为

式中 D——气隙直径；

S——气隙表面积。

对于给定的功率和转速特性，增大气隙直径D将会降低对所需表面积S和发电机尺寸的要求。如果厚度h独立于所选直径D（这个假设对于给定的转速是现实的），通过提高直径D，将会减小所需的有效体积（表面积乘以厚度，S·h）^[49]。

由于该发电机为径向磁通永磁同步发电机，它在转子内的铜损比绕线转子要小。在感应发电机中，需要一个很薄的气隙来限制励磁电流和漏磁，因此这种尺度的气隙与直径几米长的推进器缺乏可比性。

参考文献[49]中设计的同步发电机与一个脉冲宽度调制（PWM）电压变换器相连接，以控制定子的电流和转速。它可以通过电力电子接口连接到电网或者负载总线之上。

对结构设计的挑战是要实现最小气隙，这是由于到达定子表面的磁铁径向感应与气隙厚度成反比。气隙的浸没是另外一个挑战。与其他需要旋转密封的轮毂系统相比，让水流过气隙将会使得密封问题最小化^[50-52]，这将会改善发电机的散热性能。另一方面，有源元件还需要覆盖耐腐蚀涂料或者玻璃纤维加环氧树脂涂料，因为有源元件具有腐蚀性。

电磁模型决定了发电机的尺寸、额定功率和直径等主要物理参数。最有效的参数是电磁转矩T，它可以在忽略机械损耗的情况下使用式（4.101）来求得。T也可以通过假设在定子中为纯正弦波电流来计算。在式（4.101）中，A_L（A/m）为定子电流的方均根值，B₁（T）为定子表面磁通密度峰值，k_b1为线圈因数，ψ为感应电磁力和定子电流之间的矢量角。如果A_L、B₁、k_b1和ψ取固定用于低速大转矩发电机的经典值，那么就可以使用式（4.101）来确定发电机活动部件的尺寸^[49]。如果将角度设置为零，就可以将尺寸减至最小。这可能会增加变换器的尺寸和成本^[54]，但对于水下应用系统来说，这将有利于降低发电机的尺寸大小。

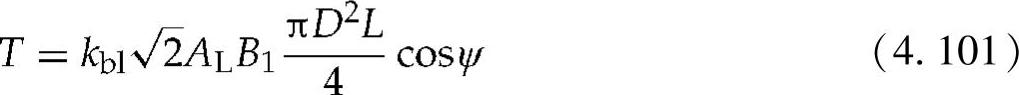
磁通密度B受磁铁类型、间隙厚度、尺寸以及经济因素的限制。该磁铁具有均匀的径向磁化，并且被表面安装在转子之上，如图4.53所示。

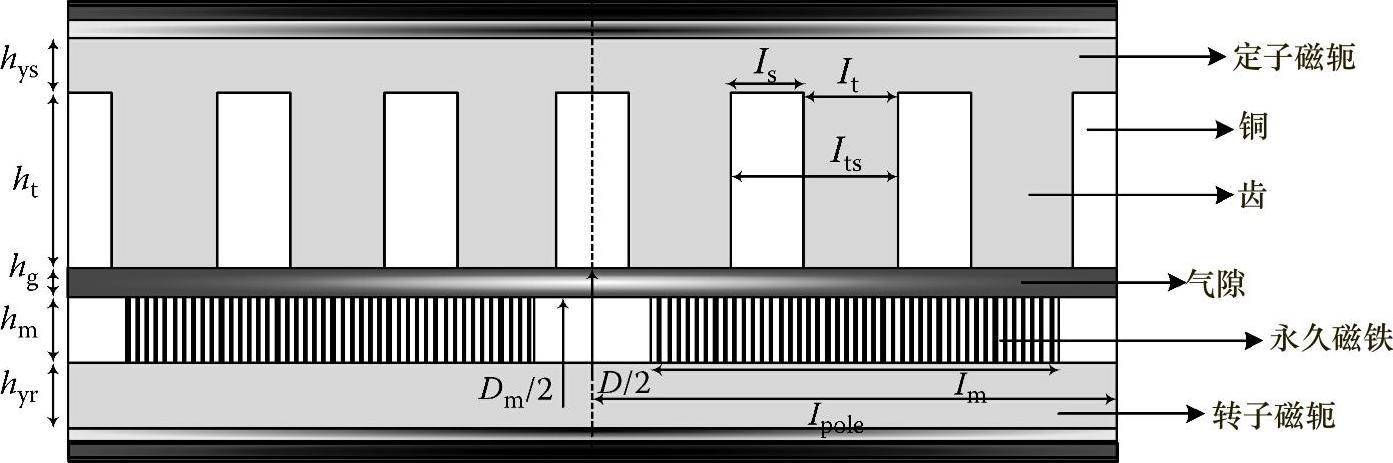
图4.53 发电机两个磁极的截面图

由于发电机的具体性能不同，为B₁找到一个作为尺寸和磁铁性能函数的简单解析表达式并不容易。相对于较短的磁极距来说，如果气隙较大，那么从一个磁铁到下一个磁铁之间将会产生不规则的漏磁。假设只有径向磁通密度也可能会产生不准确的结果。使用Zhu等人^[55]提出的二维模型，通过将极性分离并将漏磁考虑在内，可以对y轴的调节方程进行求解。它可以预测在表面安装的无齿槽永磁发电机气隙的开路电场分布。假定在比厚度大的转子直径和较大的磁极数下，B₁的表达式可以根据下式得出，并可以简化为

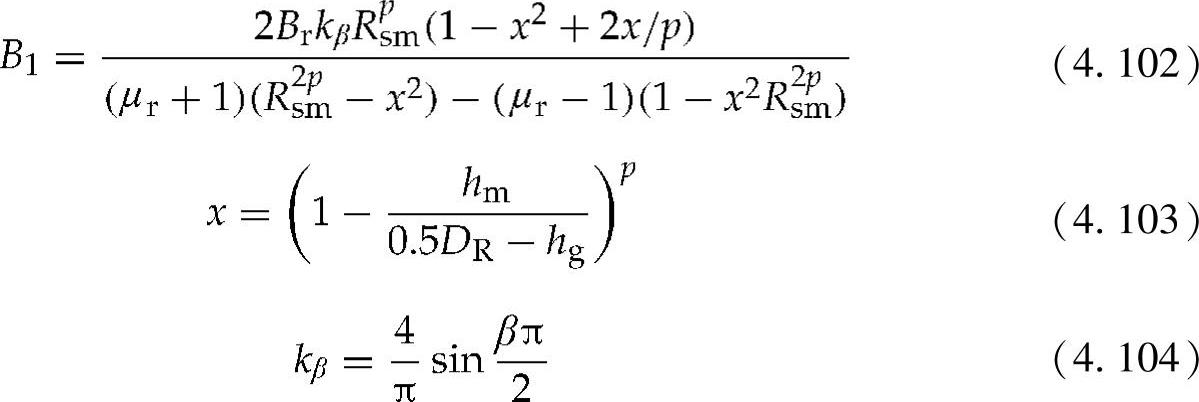
式中 B_r——磁铁的剩余磁通密度；

β——磁铁宽度与磁极宽度之比（l_m/l_pole）；

R_sm——气隙直径与磁铁外径之比（D/D_m）；

p——磁极对数；

μ_r——磁铁的相对回复磁导率；

h_m和h_g——磁铁和气隙高度。

无齿槽发电机等效值可通过卡特（Carter）因数得出^[55]，卡特因数这个参数用于考虑开槽对于气隙磁通的影响。如果B₁、p和R_sm已知，可以求出h_m来计算所需的磁铁高度。

在给定的负载电流A_L下，齿槽高度h_s可以计算如下^[54]：

式中 J——方均根电流密度，（A/m）；

k_f——齿槽填充因数；

k_s——l_s与l_t+s之比（见图4.53所示）。

电流密度J取决于热因数，在这种应用中，它可以通过环绕在发电机周围的水来改善。因此，可以降低发电机的整体厚度。

应该选择转子和定子磁轭高度以避免铁心饱和，因为它们的高度会影响气隙的大小。电工钢通常都具有约为1.7T的饱和磁通密度（B_sat）。为了限制铁损，在参考文献[49]中，B_sat被限定为1.7T。磁铁和线圈产生的磁通密度可以通过参考文献[53]中描述的经典方法来估计。

不过，由于大气隙与短磁极距之比的存在，二维有限差分仿真表明，这些方程错误地计算了相关尺寸。由于磁铁和线圈之间的漏磁比例较大，因此提高了到磁轭的磁通密度平均值。磁轭高度h_yr和h_ys可以通过迭代过程来重新调整^[49]。不过，磁轭仍然较薄和结构集成的机械限制是影响额定值的主要因素。齿宽与槽距之比（l_t/l_t+s）也可以这样估计：发电机齿不饱和，其形状也保持现实形状。一旦在固定的转子直径D_R与气隙高度h_g下计算出磁铁和转子磁轭的高度，就可以计算出气隙直径D和有效长度L。

为了限制铁损，电频率应限制在最大值f_max之内，由此可以确定最大的磁极数。系数必须保护磁体免遭退磁，尤其是在指定了较低的B₁值的情况下。这就表明，磁场在磁铁的任何点处都不能超过它的矫顽磁场^[49]。因此，必须确定最低的磁极数。

该解析模型的电气部分包括所需的发电机电压和电流水平，然后再确定发电机尺寸和线圈性能等设计参数。使用（dϕ/dt）可求得每相的反电动势，其中ϕ为单相绕组的磁通量，而且可以通过电磁转矩计算出电流：

考虑端部绕组几何因素，将每个端部绕组视作一个直径等于磁极距的半圆，也可以计算相电阻R^[56]。使用额定温度下的铜导电性，可以计算出电阻^[49]。

然后，可以计算出输出电压和功率因数，如图4.54所示。电流和电压水平会对电子驱动电路和电气网络产生影响。此外，应该确定发电机的时间常数，它是变换器开关频率的函数。

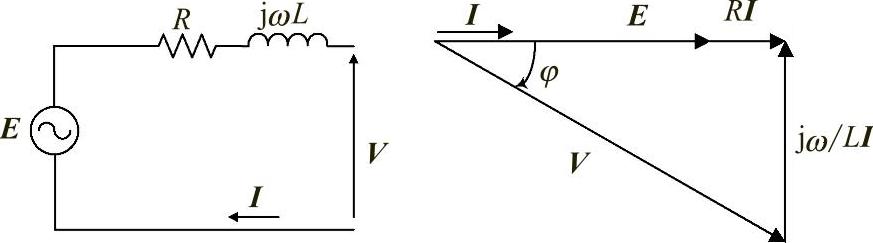
图4.54　ψ=0时的电气相量图

可以使用发电机的铜铁损和铜损来粗略估计该解析模型的损耗和效率部分。铜损与线圈电阻成正比：

P_Cu=3RI² （4.107）

该式包括了活动部分和端部绕组的损耗。如果轴向长度小而直径大，端部绕组损耗可能会增大，并会对铜损产生决定性的影响^[49]。铁损可以使用定子磁路的单位质量损耗（标幺值）来估计：

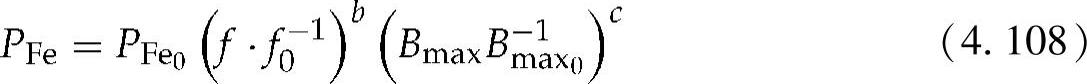
式中 f——磁场铁心的频率；

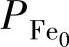——给定频率f₀下的单位质量铁损；

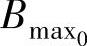——磁通密度。

对于典型的高品质铁硅层压钢来说，b和c分别为1.5和2.2。这个模型忽略了机械损耗。机械损耗受轴承技术选择的影响，该技术用来补偿水轮机的轴向阻力，并保持定子和转子之间的气隙固定。

可以使用热模型来估计发电机不同部位的温度。热模型基于稳态条件下的热传导方程来导出热阻。径向传热表示对温度的过高估计，不过它简化了热模型。此外，转子传热可以忽略不计，因为通过间隙的水流是非常好的传热平台。该系统中有两种传热模式：一种是发生在发电机固定部分的传导传热；另一种则是对流传热，它发生在定子的内外表面和海水之间。

在计算传导传热时，应考虑如图4.55所示的统一体积（Unity volume）。角宽度、内径和外径、轴向长度分别为α、R_i、R_o和l。内、外表面之间的温度差可以表示为

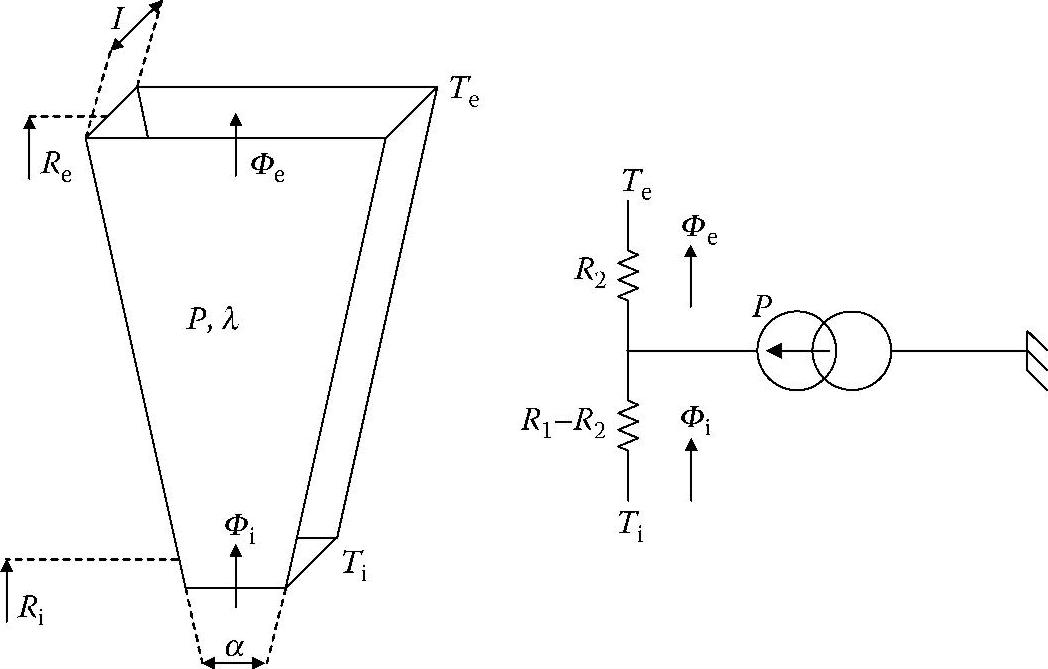
图4.55 统一体积和热等效电路

式中 T_i——内表面温度；

T_e——外表面温度；

ϕ_i——内部磁通；

P——体积损耗；

R₁、R2——热阻。

在直径较大的情况下，R₁和R₂可以表示为

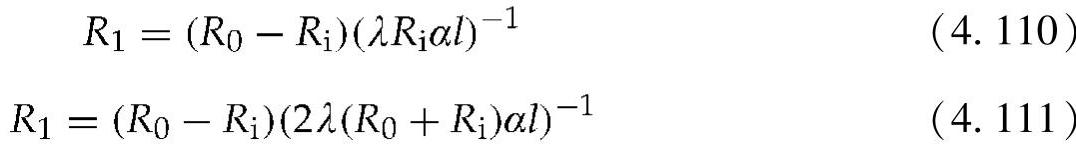
式（4.109）对应着图4.55所示热网络的电气表示。

对流热交换模型中使用的表面电阻为

式中 S——热交换表面积；

h——对流传热系数。

4.3.5.5 用于海洋WEC的感应发电机

在WEC系统中，最后一个转换环节是由发电机来完成的，它将机械能转换成电能。一般来说，WEC系统使用的是变速水轮机。变速会产生变频输出，而且系统将需要一个变频器，如果是使用同步发电机，也就是一个与逆变器级联用于并网的整流器^[57]。使用同步发电机的缺点可能是需要一个变速恒频逆变器系统用作发电机与电网之间的接口。而且它还需要一个自动同步系统，以便在供电期间实现发电机输出与电网同步。此外，为提供励磁电流，还必需一个可变直流电源。如果不使用永磁发电机，那还需要电刷。集电环电刷需要定期维护。

另一方面，以超同步转速运转的感应发电机还可以向电网提供电能^[57]。使用感应发电机还可以省掉变频器、直流励磁以及同步机构。此外，感应发电机没有电刷，它们使用能够以更高转速运行的笼型转子。同时，感应发电机需要一个简单的控制机构，而且它们更便于并网运行。不过它们需要来自电网的无功功率，为发电机提供励磁和磁化。在单机应用中，应该使用大型电容组与定子绕组并联，以此来为感应发电机提供无功功率。

为确保感应发电机在WEC系统中的使用，还有一些注意事项^[57]。

在电网出现故障时，电输出功率将下降到零，但机械能仍将被作用到具有加速转矩的发电机上。因此，水轮机的转速将会增加，而且必须进行机械保护。发电机应免受海水和大气腐蚀作用的影响。发电机受限于海水波浪的溅泼，因此内部绕组和其他部件需要使用外壳来保护。必须将感应发电机设计成可用于更高的转速变化范围，以便与气动涡轮机相耦合。

感应发电机非常适合与威尔斯水轮机耦合使用。威尔斯水轮机可以分为两种类型：自起动威尔斯水轮机和非自起动威尔斯水轮机。根据水轮机类型的不同，感应发电机耦合和需求可能也会有所不同^[58]。在自起动发电机应用中，感应发电机不需要通过初始运动激励，而非自起动水轮机则需要使用外部供能的感应发电机或其他发电机曲柄。

感应发电机是业内最为常用的电气装置之一。在有功功率电力电子器件发展之前，通常使用固定电容来为感应发电机励磁提供无功功率，这并不是一种灵活的解决方案，因为无论是负载还是转速偏差如何，其方位总保持不变^[59]。如果感应发电机与大型电力系统一起使用，可能会由电网提供励磁，在该电力系统中，可用无限大容量母线。感应发电机运行必须使用可调励磁方式，并使用电力电子开关器件进行适当的隔离控制。

感应发电机的结构包括两个电磁部件：第一个部件是使用高电导率和高强度的线棒构造的旋转磁场，它被放置于开槽铁笼内；第二个部件是定子绕组和定子铁心。图4.56所示为一个典型的感应发电机的横截面视图^[59]。

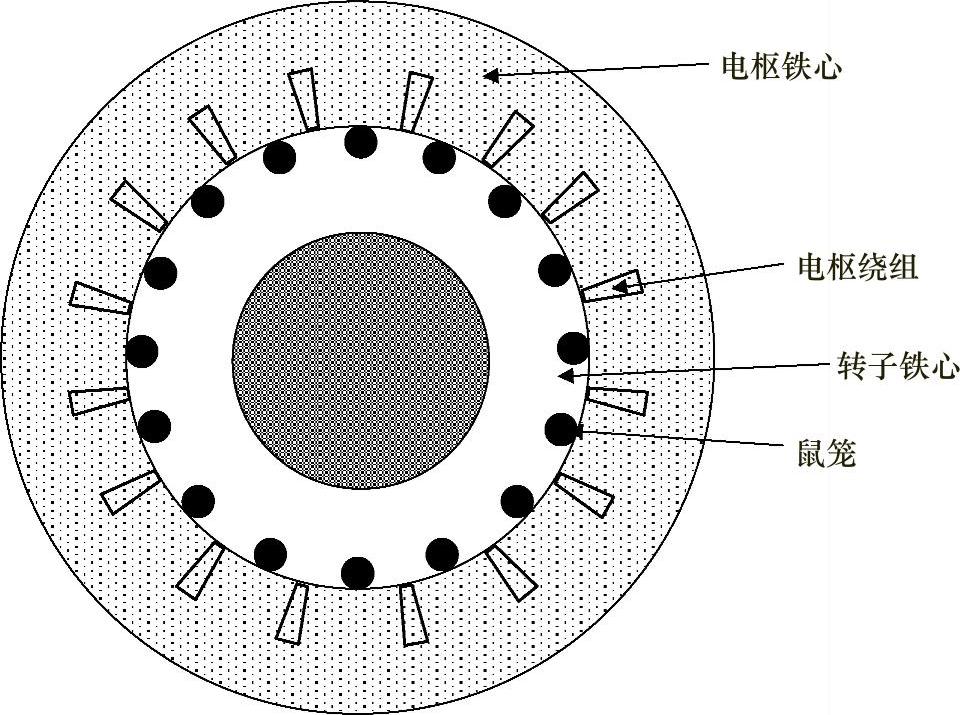
图4.56 感应发电机结构的横截面视图

该感应发电机的输出为三相交流形式。可以通过调节励磁电流来控制电压，以保持输出电压恒定^[59，60]。因此，无论负载电流和转速如何变化，输出电压可以保持固定不变。可以使用一个控制器来控制励磁电流的幅值与频率。应给固定绕组提供励磁电流，该电流可以通过固定绕组导入短路转子绕组。

在一个感应发电机中，转子的同步转速和角速度可以表示为

式中 n_s——每分钟的同步转数；

f_n——额定频率；

p——磁极对数；

ω_m——转子角速度。

水轮机产生的机械转矩驱动转子轴，而该机械转矩产生的发电机的机械输入功率为

式中 P_m——机械输入功率；

T_m——机械转矩。

角速度的导数为

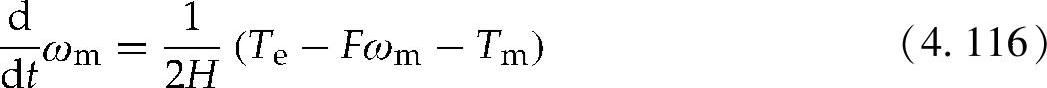
式中 H——转子和惯性组合常数；

T_e——电磁转矩；

F——转子和水轮机摩擦力组合常数。

应该指出，此式对感应电动机和感应发电机的运行均有效。T_m在发电机运行模式下为负值。

角转子位置为

定子绕组的感应电压和端电压之间的关系如下：

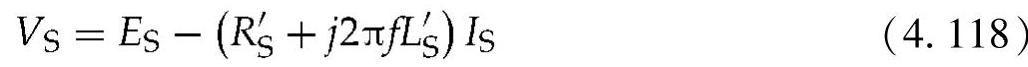
式中 E_S——每相感应的定子电压；

R′_S和L′_S——转子和定子组合电阻和电感；

I_S——定子电流。

感应发电机的视在输出功率可以写为

该发电机的有功功率输出可以通过下式计算：

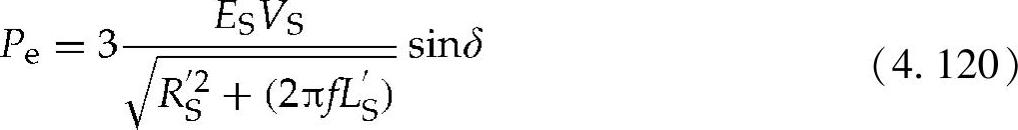
式中 δ——V_S和E_S之间的功率角。

4.3.5.6 用于海洋WEC的开关磁阻发电机

直线和旋转开关磁阻（SR）发电机适应于海洋波浪应用系统，因为它们既没有电刷，也没有转子绕组。因此，它们需要的维护工作量较少，而且更易于维护。永磁发电机也非常适合于海洋WEC应用，不过它们成本更高，而且尺寸相对较大。

SR发电机的概念基于被磁性充电的相反两极的吸引^[61]。定子和转子的凸磁极数通常并不相等。建造它们使用了电工级薄板钢。

开关磁阻发电机（SRG）的横截面视图如图4.57所示^[59]，其中，有8个定子磁极和6个转子磁极。也有可能使用10/8和12/10的定子和转子磁极组合。

SR发电机转子没有使用绕组。电枢线圈相互隔离，它们是同心的，而且位于定子磁极上^[59]。当两个相反磁极上的线圈被励磁（比如转子磁极A-A和定子磁极1-1），相应的定子磁极就会被磁化。如果原动机反方向驱动转子，定子线圈中就会产生电压，从而产生了电能。

SR发电机的输出电压是带有高纹波的直流电压，它应该通过控制励磁电流持续时间来进行滤波和调节。

直线SR发电机也适用于海洋WEC的应用场合。

图4.58所示为一个直线开关磁阻发电机的横截面^[62]，其中转换装置（运动部分）被放置在两个定子侧（固定部分）之间。该发电机是一台4/6发电机，这意味着每6个转换器齿配有4个定子齿。除了4/6发电机以外，还可以使用6/4结构设计，不过4/6结构允许在定子内给铜线圈留出更多的空间。

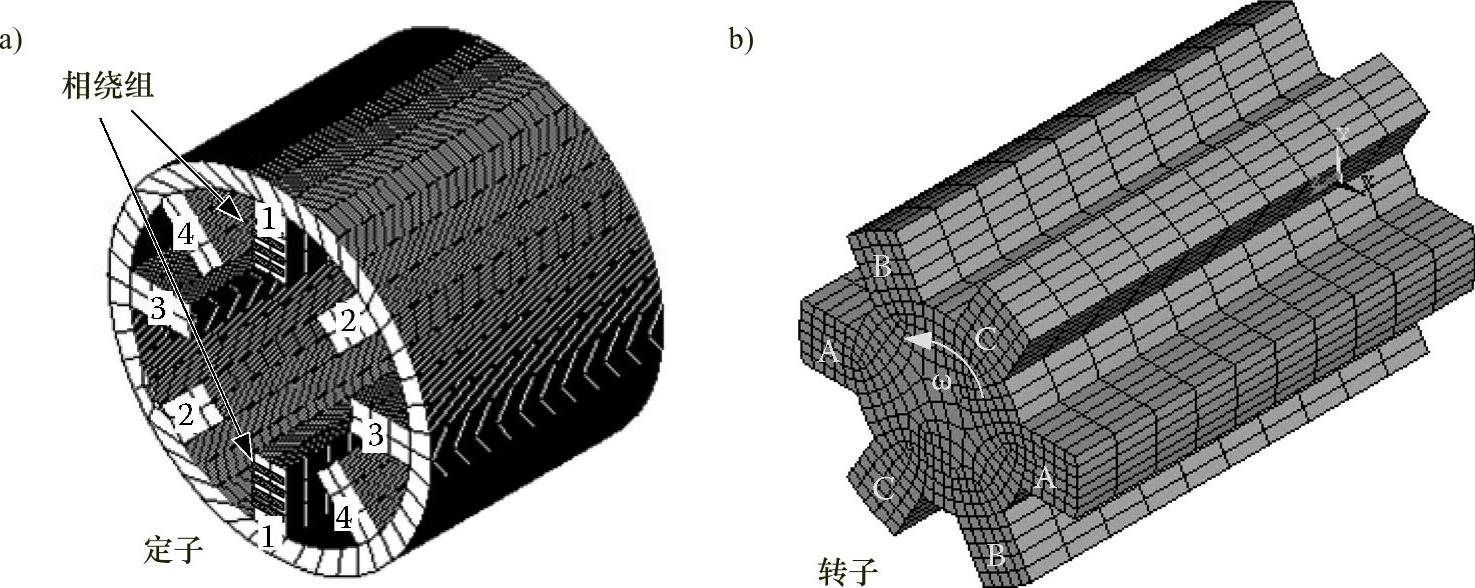
图4.57 8/6磁极开关磁阻发电机的横截面视图

a）开关磁阻发电机定子 b）开关磁阻发电机转子

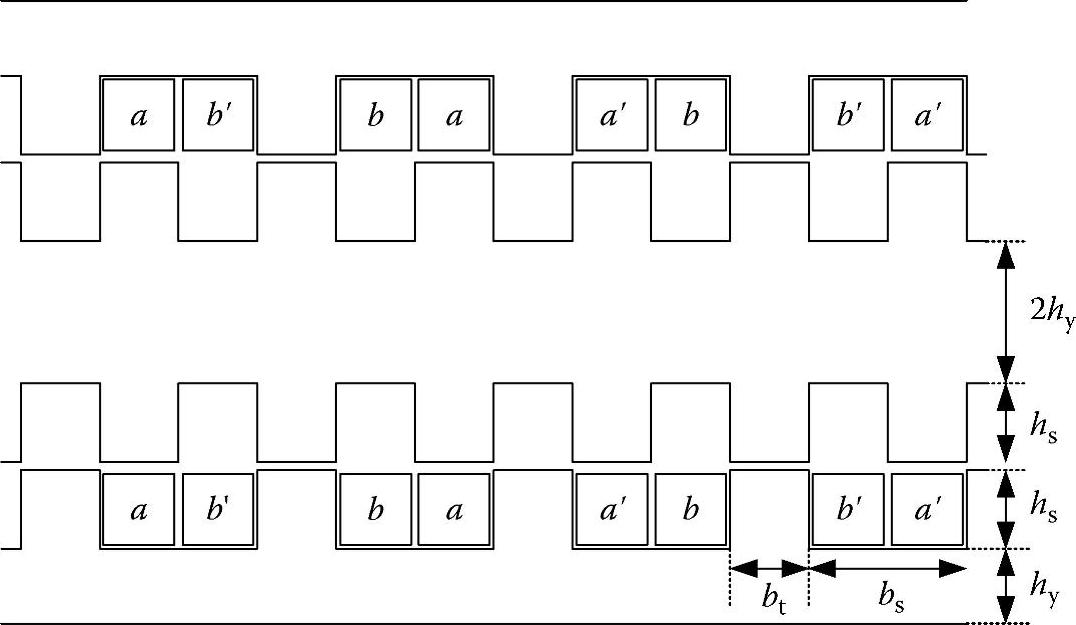
图4.58 直线开关磁阻发电机的横截面视图

在对齐的位置上，定子齿面直接面对着转换器齿，在非对齐位置上，它们并不相互直接面对。在对齐位置上，电流增大到所需的水平，并在不对齐的位置逐步下降为零^[62]。在对齐位置上，磁通密度被限制在饱和水平。未对齐位置上的磁通量要低于对齐位置的磁通量。可以使用磁链—电流图的能量转换面积来计算平均作用力^[63]：

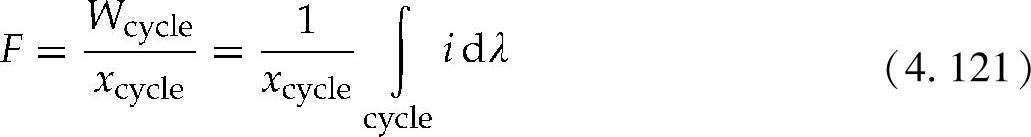
式中 W_cycle——一个周期内转换的能量，通过磁链—电流回路面积计算而得；

x_cycle——一个周期内的位移；

λ——磁链。

4.3.5.7 使用压电/电致伸缩材料的海洋能源转换

除了使用直线发电机或者传统的旋转发电机，还可以在WEC应用系统中使用压电/电致伸缩材料。Taylor等人^[64]研发了一款名为“能源发电Eel”的新装置，该装置将海洋波浪能转换成电能，为位置偏远的用于海洋测量和采样网络的传感器或者相关设备供电。这种能源采集方法使用了在水流中波动的压电聚合物长条。

图4.59说明了如何利用平台和固定机构将压电聚合物安放在海底^[64]。

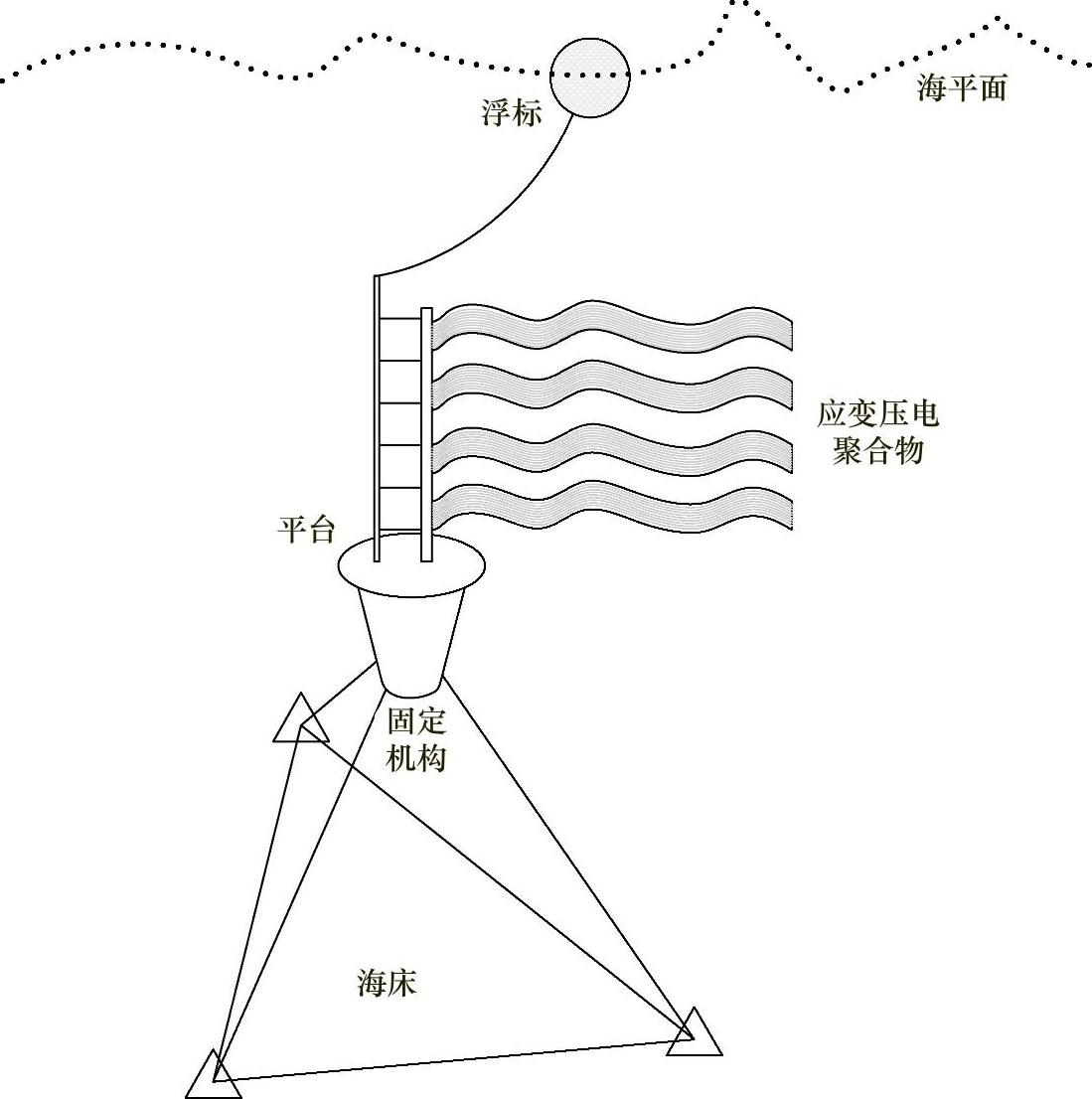
图4.59 固定在海底的Eel系统结构

图4.60所示为影响Eel的作用力示意图。

根据钝体（非流线型阻流体）的流动速度及其宽度，钝体在其两侧产生频率不同的交替涡流，涡流引起的压力差造成了Eel的摆动。由于在压电聚合物上产生了应变，压电聚合物沿着段电极产生了一个低频交流电压^[64]。这种电压可以被转换为直流电，用于近岸输电，或者为电池充电，或者为海洋设备或传感器供电。

Eel内部为多层结构。非本质（non-native）中心层（核）和与中心层两侧相结合的活性层压电材料构成了典型的三层结构。该中心层是一个柔韧的厚层聚合物，这种柔韧的结构增大了围绕其他层运动的弯矩。压电材料或者电致伸缩材料用于构建发电层。活性层中的应变应该达到最大化，以获得更多的功率^[64]。

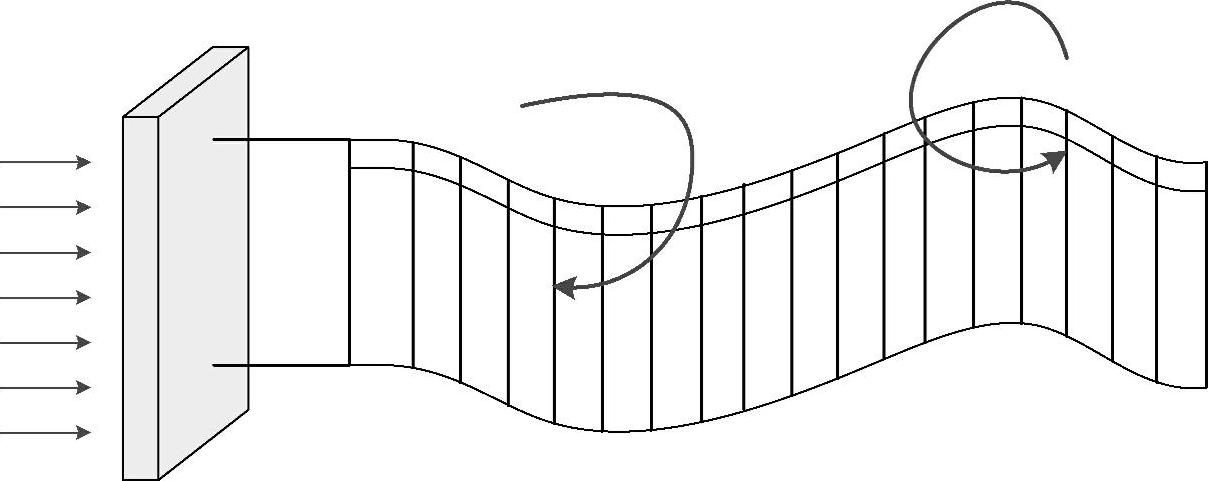
图4.60 钝体后面的Eel运动

Eel在水中波动起伏产生的电能P可通过下式计算：

式中 η₁——水力效率，它取决于Eel的振荡频率以及钝体后面的涡街频率，如果这两个频率相互匹配，水力效率就会提高；

η₂——转换成压电聚合物中电能的应变转换效率；

η₃——从压电聚合物中提取电能的效率，它是由谐振电路提供的；

A——截面积；

ρ——水的密度；

V——水的流速。

Eel流量驱动的振荡类似于有风天气柱子后面的旗帜^[65]。通过直观地记录流槽中的Eel曲度，以及电测得出的段电极开路电压，可以计算出应变^[64]。Eel运动可以被描述成一个自然频率模式的总和，或者描述成一个行波。通过改变钝体宽度或流量的雷诺数可以修改Eel系统参数，从而影响Eel的运行。

可以使用压电聚合物将水流的机械能转换成电能。从单位体积的压电材料中可以获得的能量P_o（标幺值）为

式中 d₃₁——压电材料的机—电耦合参数；

s——材料机械应变的百分比；

γ——材料的弹性模量；

ε——材料的介电常数；

f——材料的应变频率。

机电耦合效率由下式给出：

在Eel内已经使用了聚偏氟乙烯这种压电聚合物。该聚合物具有如下优点：它可以耐多种化学品，而且机械强度较高。此外，它们还可以制成连续卷状，这使得它们能够以较低成本制成宽度和长度不同的形状。在Eel应用系统中使用聚偏氟乙烯聚合物的惟一缺点是它的压电常数d₃₁相对较低。这将导致Eel的转换效率（k₃₁）较低，进而输出功率（P_o）较低^[64]。

电致伸缩聚合物是用于Eel的传统压电聚合物的替代材料，它的性能更好。通过保持高直流偏置场，有可能感应出一个大的压电场。感应压电效应是由电介质中麦克斯韦应力产生的结果。应用于直流偏置聚合物的交流机械应力可引起电致伸缩介质的尺寸差异。因此，通过附着在聚合物表面的电极，就可以产生电荷的交替流动。对于电致伸缩聚合物，有效的d₃₁可以定义为

因此，效率k₃₁变为

式中 V——产生的交流电压；

th——电致伸缩聚合物的厚度。

电致伸缩聚合物的d₃₁和k₃₁要比聚偏氟乙烯这种压电聚合物高得多，因此，它的输出功率（P_o）也高得多。当电致伸缩聚合物具有较高的k²₃₁值时，它们就可以采集更多的能量^[64]。

不过，电致伸缩聚合物也有一些缺点，比如机械强度较弱、电击穿强度较低、介电损耗较高，而且还缺乏具备所需特性的商用资源。这些缺点使得在Eel中使用电致伸缩聚合物不切实际。

开关谐振能量转换技术用于从聚合物中提取电能。当压电装置作为发电机使用时，使用电气和机械谐振系统，能够克服低耦合系数k²₃₁=d₂³¹（γ/ε）。Eel的运动频率非常低，如1～2Hz，因此采用直接电谐振方式是不现实的，因为它需要非常大的电感值。因此，开关谐振能量转换可以克服这种局限。这种转换技术能够使用合理的电感值在1～2Hz范围内高效运行^[64]。

图4.61所示为用于Eel能量采集的开关谐振能量转换器的电路原理^[64]。

在这个电路中，R_P表示压电材料（PVDF）的介质损耗电阻，C_P为Eel电容，V_OC为与应用应变相对应的Eel的开路电压^[64]。Eel可以使用这三个基本要素进行仿真。其他电路部件属于外部能量转换电路。它们是指开关（S）、电感（L）与串联绕组电阻（R_S），R_L代表负载电阻。

假定压电部件的输入是一个正弦波源。开关S在该输入的正负峰值时打开，其周期正好等于L-C_P网络谐振周期的一半。该开关的闭合时间为

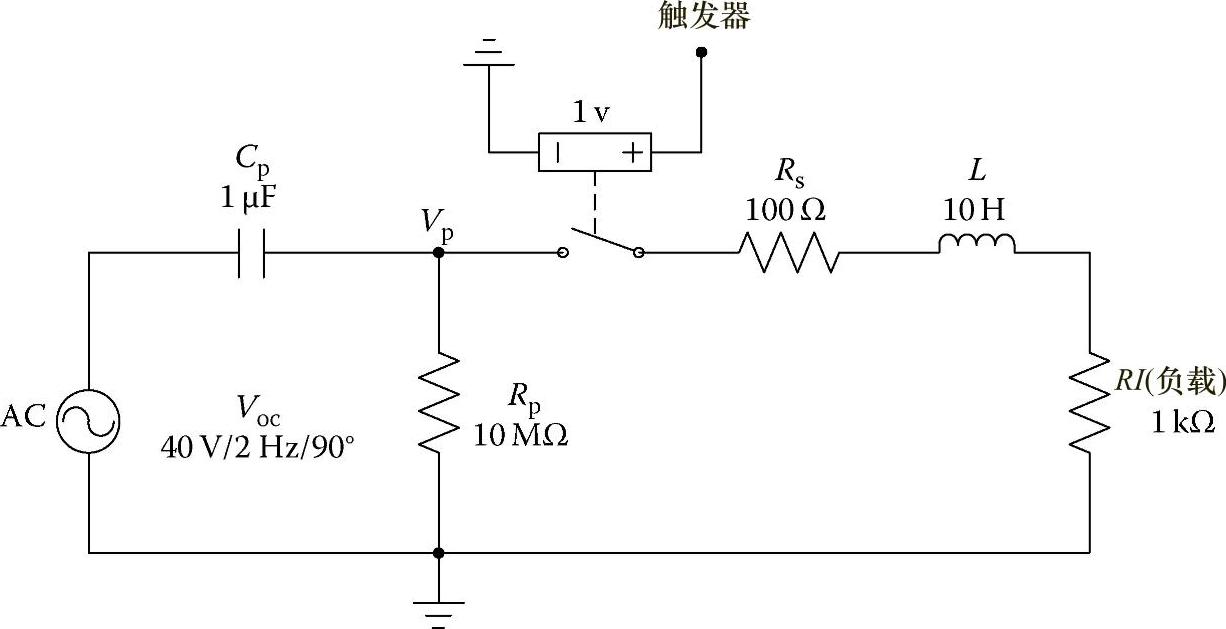
图4.61 开关谐振能量转换器

对于给定的典型值来说，T_C等于7.18ms。闭合区间的电压可由下式计算而得：

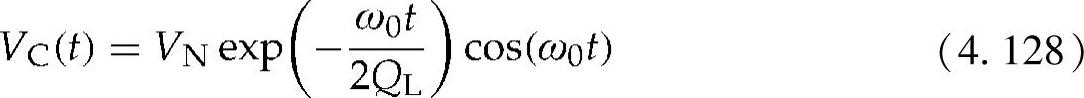
电容C_P上的初始电压V_N，其中

以及

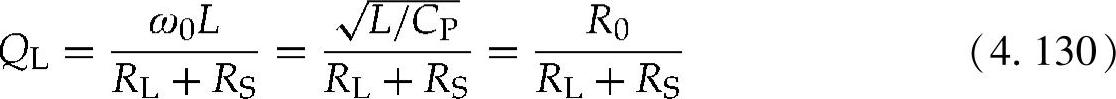
在此闭合期间的电感（L）电流可由下式计算而得：

在t=T_C时，开关S打开，电压变为

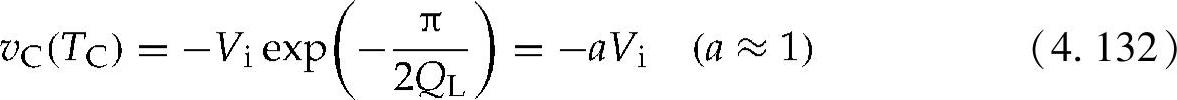
和

当开关打开时，“a”被定义为

该开关将保持开启状态，直到产生下一个峰值（负）为止，然后再重新关闭。在开关开启期间，VC将持续充电（负），因为发生应变的压电部件会产生一个电荷^[64]。在此期间V_C（t）的变化为

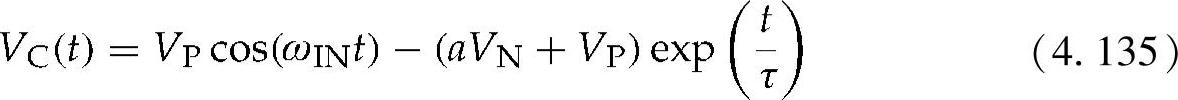
其中压电介质损耗网络的时间常数为

而且，V_P为开路电压峰值。S在下一个相同周期T_C的峰值时关闭，而且其行为也与之类似，除了现在的（V_i）+值更高以外。在下一个关闭周期的

之前电压V_C值达到V_N+1，它可以表示为

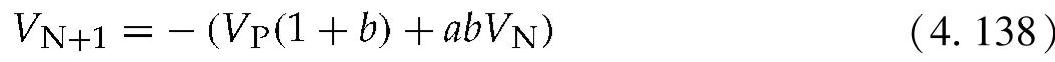
在式（4.138）中

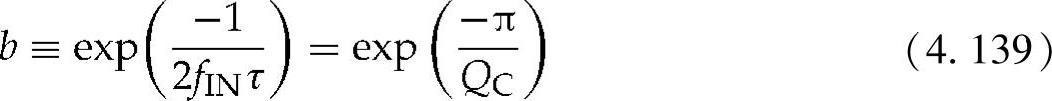
其中

这个过程每半个周期重复一次，直到达到稳态条件为止。应当指出，波形的极性每半个周期变化一次。当传输给负载R_L的电能加上感应器、电极和PVDF介电的损耗，被通过压电装置增加的能量所偏置时，达到稳定状态。

式（4.138）允许递归预测建立电压以作为输入的半周期数。电压的建立大约需要Q_L周期。传输给负载的稳态能量可以通过稳态电压来确定。通过式（4.138）将V_N+1设置为V_N可以求得稳态电压，由此得出

在负载上施加一个由峰值电压产生的半正弦电流波。电流脉冲宽度为T_C，而且振幅峰值可以写为

因此，平均输出功率可以表示为

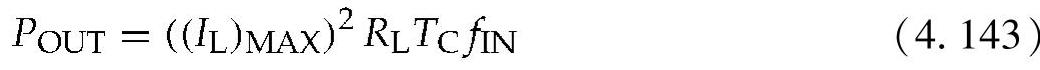
跨无功组件的高压建立取决于开关谐振能量转换器中的Q。在这种开关技术中，谐振频率和输入频率可以不同，这是这种电路最为重要的优势，这样就有可能降低元器件的额定值。

如果损耗元件实现了最小化，那么就可以实现输出功率的最大化。损耗是由电感的绕组电阻、电极电阻和电介质所引起的。正如在其他谐振系统中，采用R_L的最优值就可以实现功率输出的最大化。通过式（4.131）～式（4.133），可以得到R_L的最优值。如果假设对于Q_L和Q_C（＞5）的较大值，参数a和b均为1，因此（V_C）SS的稳态值可以改写为

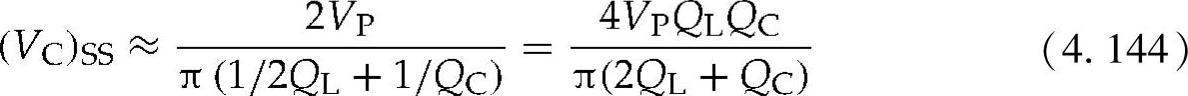
因此，功率输出可写为

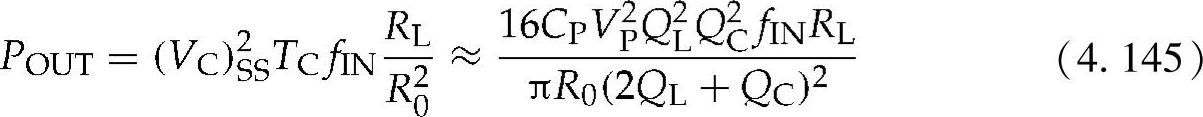
机械输入功率为

其中，机械耦合因数可以计算为

因此，能量转换效率可以描述成P_OUT/P_IN之比：

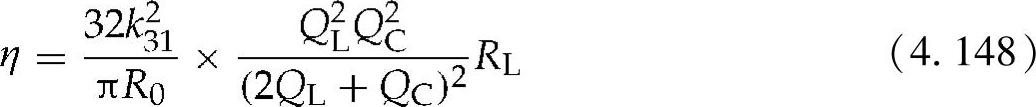
Q_L可以使用R₀/（R_L+R_S）来代替，并根据R_L实现最大化，R_L的最优值为

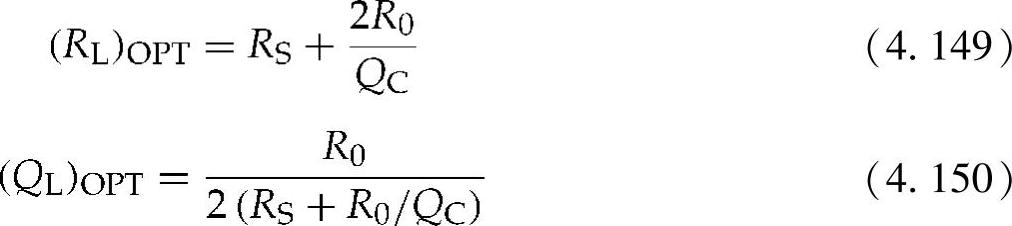
对式（4.149）和式（4.150）进行积分，可以得出转换效率的最大值为

使用图4.61给出的典型参数值，可以计算出基于压电聚合物的海洋能发电的最高效率为37%。